Промышленное освоение территории и недр в районах многолетней мерзлоты (криолитозоны) неизбежно приводит к нарушению естественного процесса тепло-массообмена грунтов с атмосферой. В строительстве горных выработок в криолитозоне для уменьшения или предотвращения протаивания мерзлых горных пород с целью повышения их устойчивости обычно используются теплозащитные крепи и системы [1, 2].
Исследованиям систем и методики регулирования теплового режима горных выработок в криолитозоне посвящены научные разработки Института горного дела Севера СО РАН [3, 4]. Однако предложенные методики не дают полной возможности полноценного решения всех разновидностей задач теплофизики для горных выработок в условиях криолитозоны [5]. Например, при расчете вентиляционных систем шахт и рудников не всегда в полной мере учитываются особенности теплообмена воздуха с вмещающим массивом горных пород, фазовых переходов в них в процессе изменения теплового режима подачи воздушных масс.
Математическое моделирование тепловых процессов в горных породах и выработках позволяет оценить не только их криогенность, устойчивость, прочность и другие параметры для производства горных работ [6, 7], но и установить эксплуатационную эффективность использования теплоизоляционных материалов в составе теплозащитных крепей.
Целью исследовательской работы является разработка инженерного метода определения оптимальных параметров теплоизоляции горных выработок в условиях криолитозоны на основе результатов математического моделирования.
Материалы и методы исследования
В условиях криолитозоны основным условием обеспечения устойчивости подземных сооружений является сохранение вечномерзлого состояния вмещающих горных пород в течение определенного срока их эксплуатации. В основном для управления тепловым режимом вмещающих многолетнемерзлых горных пород используются эффективные теплоизоляционные материалы (легкие бетоны с пористыми заполнителями и полимерные теплоизоляционные материалы) [8]. Выбор материала и толщины теплоизоляции определяется из условия недопущения или сохранения глубины протаивания многолетнемерзлых пород в заданный период эксплуатации.
Ниже приведены результаты математического моделирования тепловых процессов в подземных выработках криолитозоны с учетом фазовых переходов в многолетнемерзлых горных породах. Разработанные модели с достаточной точностью позволяют решить актуальные задачи эффективности использования теплоизоляционных материалов для снижения глубины протаивания, а также условия, не допускающие оттаивания мерзлого грунта, в определенный срок эксплуатации горных выработок в условиях криолитозоны.
Математические модели также могут использоваться для оценки эксплуатационной эффективности теплоизоляционных материалов в составе конструкций крепежных элементов с целью сохранения устойчивости горных выработок криолитозоны.
Результаты исследования и их обсуждение
1. Алгоритм для определения оптимальной толщины теплоизоляционного слоя, не допускающего оттаивания
Распределение температуры в горных породах вокруг подземных сооружений в толще многолетней мерзлоты с высокой вероятностью может быть описано линейным уравнением теплопроводности
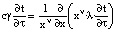, x∈(r0, R), τ > 0. (1)
Допустим, что в исходный момент времени t = 0 многолетнемерзлый массив имеет температуру
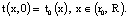(2)
Допуская, что R – достаточно большая величина, граничное условие при х = R можно задать в следующем виде
t(R, τ) = t0(R), τ ˃ 0. (3)
Предполагая, что заданный теплоизоляционный слой рассматривается как термическое сопротивление, граничное условие при x = r0 будет иметь вид
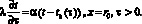(4)
Здесь
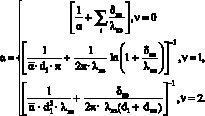(5)
Далее следует уточнить значение величины α, удовлетворяющей требованиям
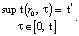(6)
где t* – показатель температуры, при которой мерзлые горные породы переходят в другое фазовое состояние (оттаивание льда в горных породах).
Следует отметить, что искомая функция t(x, τ) зависит от α, поскольку управление температурным полем горных пород проводится изменением α. Таким образом, уравнение (6) следует изменить на другой вид
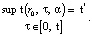(7)
Далее следует уточнить постоянную α – корень трансцендентного уравнения (7), где t(r0, τ, α) – значение решения краевой задачи (1)–(4) при х = r0, t ˃ 0.
Решаем поставленную задачу с применением метода «секущих»:
а) задавая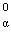 
и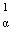 
допустим, что s = 0;
б) решается краевая задача применительно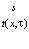 
c α = 
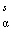
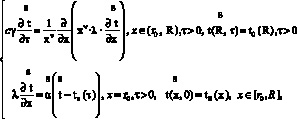(8)
в) определяем
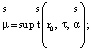
г) увеличиваем s на одну единицу s = s + 1;
д) при s = 1 переходим к решению пунктов б–г;
е) решаем методом «секущих» заданное приближение значения коэффициента теплопередачи:
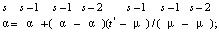
ж) проводим проверку условия
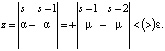
При z ˃ ε возвращаемся к решению пунктов б–ж. Иначе
α =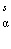 
, t(x,