Задача оптимизации распределения ресурсов возникает в различных областях, таких, как минимизация времени при выполнении заказов, распределение рекламы на телевидении для максимизации получаемого отклика [1], минимизация нагрузки оборудования для интернета вещей (IoT) [2] и т.д. Показано, что она относится к классу NP-полных задач [1], поэтому разработка оптимизированных подходов к ее решению является актуальной и практически значимой. Развитие метода агентного моделирования [3] привело к широкому использованию мультиагентных систем как технологической платформы для реализации недетерминированных конечных автоматов в виде программных агентов.
В настоящее время представляют интерес задачи с динамически изменяющимися условиями в процессе решения. В этом случае практически неприменимы ранее разработанные способы решения задачи распределения ресурсов с помощью линейного программирования.
Решение распределительных задач на основе использования мультиагентной системы позволяет учитывать динамические особенности задач, возникающих на практике. Одним из направлений исследований является формирование коалиций агентов для совместного достижения общей цели, которая не может быть достигнута каждым агентом по отдельности [4]. Коалиционный подход представляется перспективным, но приводит фактически к новому классу распределительных задач, что требует дополнительного изучения. Предлагаемый в настоящей работе подход к решению задачи разбивается на несколько этапов: формирование коалиций агентов, решение модельной задачи разработанным и известным оптимальным алгоритмами на входных данных, для которых применим оптимальный алгоритм, оценка близости полученных решений.
Задача и алгоритмы формирования коалиций
Задача формирования коалиций определяется следующим образом. Пусть имеется конечное множество агентов А и характеристическая функция f(А), которая каждой коалиции (т.е. подмножеству агентов) из А ставит в соответствие числовое значение. Целью является разбиение множества агентов А на коалиции А1, А2, .. Аm таким образом, чтобы максимизировать суммарное значение характеристических функций для полученных коалиций ∑ f(Ai) → max [5]. Задача формирования коалиций агентов является NP-полной [6], поэтому точное решение возможно только для нескольких десятков агентов, для большего числа применяются приближенные алгоритмы.
Рассмотрим особенности некоторых алгоритмов, предложенных к настоящему времени.
В алгоритме [7] все возможные коалиции и связи между ними представляются в виде многоуровневого графа. Узлы графа – коалиции, ребра – соединяют те узлы, коалиции в которых отличаются ровно на один элемент. В работе доказано утверждение, что если из графа удалить ребра, оставив только ровно одно, ведущее к каждой вершине, то оптимальное решение все равно будет найдено. Таким образом, можно не вычислять все возможные состояния, а ограничиться одним переходом к соседней коалиции (т.е. одним ребром). Алгоритм способен находить решение для 25 агентов. Время работы алгоритма оценивается как О(3n).
Алгоритм IP способен работать на нескольких вычислительных узлах [6]. Благодаря тому, что коалиции хранятся в двоичном представлении и вычислительные узлы имеют уникальные идентификаторы, становится возможным не передавать список всех коалиций каждому вычислительному узлу. На основании этой информации любой вычислительный узел может самостоятельно выделить подмножество коалиций, которое он должен обработать, таким образом, не требуется дополнительной координации между вычислительными узлами. Для каждого подмножества коалиций вычисляются оценки и отсекаются коалиции, которые гарантированно не смогут увеличить значение коалиции. Вычислительные узлы обмениваются между собой этой информацией, и каждый вычисляет общее среднее и максимальное значения весов коалиций, при этом в соответствии с полученными оценками отсекаются все бесперспективные решения. Алгоритм является итерационным. Однако время работы алгоритма в самом плохом случае составляет О(nn). Эксперименты были проведены для 28 агентов.
Для нахождения решения задачи формирования коалиций для числа агентов в несколько сотен или тысяч могут быть использованы только приближенные алгоритмы. Одним из недавно разработанных является алгоритм C-Link [5]. Он основан на использовании функции взаимозависимости, которая определяет «выигрыш» от объединения двух выбранных коалиций в одну. Функция состоит из супераддитивной (возрастающей) и субаддитивной (убывающей) частей. Таким образом, на некотором этапе процесса формирования коалиций возможны «потери» от объединения коалиций агентов в одну, что ограничивает количество агентов в каждой коалиции. На первом шаге работы алгоритма «коалиция» содержит одного агента. Затем на каждом шаге определяются две коалиции, которые дают наибольший выигрыш при объединении их в одну. Эти коалиции объединяются, и процесс повторяется. Алгоритм останавливается, когда не удается найти кандидатов на объединение. Авторы установили, что для количества агентов не более 25 (которые может обработать оптимальный алгоритм IP), близость полученных решений к оптимальным составляет около 90 %. Алгоритм был протестирован для 2732 агентов, время работы составило несколько минут.
Обобщением задачи формирования коалиций является класс задач Coalitional Skill Games (CSG) [8]. У агентов имеется некоторый набор навыков. При объединении агентов в коалицию их навыки объединяются. У заданий есть набор требований к навыкам, которыми должна обладать коалиция агентов для того, чтобы коалиция могла их выполнить. Требуется сформировать такие коалиции агентов, чтобы выполнить максимальное количество заданий. Задача во многих случаях является NP-полной [8, 9]. В работе [10] для решения задач класса CSG был использован генетический алгоритм. Оценивалось время работы алгоритма, но анализ оптимальности не проводился. Авторы работы [11] предложили решение путем агентного моделирования с использованием мультиагентной системы. Авторы измеряли количество сообщений, которыми обменивались агенты, для формирования коалиций. В то же время анализ оптимальности полученного решения не проводился.
Таким образом, к настоящему времени созданы алгоритмы формирования коалиций агентов для разных классов задач. Точное решение возможно только для нескольких десятков агентов, для большего числа применяются приближенные алгоритмы. На основе полученных коалиций далее решается распределительная задача.
Подходы к решению распределительной задачи с применением коалиций
Одной из хорошо разработанных подзадач распределительных задач является транспортная. В настоящей работе решается динамическая распределительная задача перевозки однородного ресурса от источников в приемники, в которой возможно изменение характеристик агентов.
В классической постановке транспортной задачи, если суммарное количество имеющегося у источников и требуемого приемниками ресурса равно, то она является задачей линейного программирования. Известно несколько алгоритмов оптимального решения открытых и закрытых транспортных задач, минимизирующих суммарную стоимость перевозок [12].
В настоящей работе модельная транспортная задача формулируется следующим образом.
Заданы:
1) m источников с количеством имеющегося ресурса ai, i = 1..m;
2) n приемников с потребностью в ресурсе bj, j = 1..n;
3) ai < bj, для всех i и j; (1)
4) Σi ai ≤ Σj bj;
5) матрица стоимости cij > 0 перевозки из источника i в приемник j;
6) вспомогательная функция 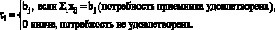
Требуется найти xij ≥ 0, такие что:
1) Σj τj → max (в случае Σi ai = Σj bj выполняется равенство Σj τj = Σj bj); (2)
2) Σi Σj cij∙xij → min (минимизация общей стоимости перевозки).
В случае если количество ресурса у каждого источника меньше потребности любого приемника (условие в п.3), то необходимо формировать коалиции источников для удовлетворения потребности каждого приемника. Характеристической функцией W является сумма количества ресурсов тех источников, которые входят в состав коалиции:
W = Σi ai ∙ σ,
где 
Возмущающими факторами в процессе моделирования решения задачи являются:
1. Изменение количества источников случайным образом.
2. Изменения имеющегося ресурса у источников случайным образом.
Алгоритм решения распределительной задачи с применением коалиций
Для описанной модельной транспортной задачи был предложен распределенный алгоритм на основе жадного решения поставленной задачи [13].
1. Приемники сортируются в порядке уменьшения потребности ресурсов.
2. Для каждого приемника все доступные источники сортируются по увеличению значений cij и по уменьшению имеющегося ресурса.
3. Если суммарное количество ресурса у источников превышает потребность приемника, то часть источников из начала списка формируют коалицию для удовлетворения потребности этого приемника. Значение количества ресурсов в этих источников становится равным 0.
4. Если суммарное количество ресурса у источников недостаточно, то алгоритм сообщает о невозможности удовлетворения потребности этого приемника и переходит к следующему.
Алгоритм останавливается, если либо потребности всех приемников удовлетворены, либо если суммарное количество ресурса, оставшееся у всех источников, меньше потребности приемника с наименьшим ее значением.
Важным свойством предложенного алгоритма является то, что информация о числе источников и количестве имеющегося у них ресурса обновляется при переходе к следующему приемнику. Таким образом, допускается динамическое изменение количества и свойств агентов в процессе моделирования.
Предложенный алгоритм был реализован с использованием мультиагентной системы SPADE. Было установлено, что время работы программной реализации для 20 источников и 100 приемников составляет около 5 минут на персональном компьютере Intel Core i5 2,6 GHz, 4 Gb RAM, Win7 [13].
Проведение вычислительного эксперимента
Поскольку теоретическое доказательство близости решения к оптимальному является затруднительным, то в настоящей работе предлагается применение вычислительного эксперимента, связанного с моделированием решения задачи при различных входных данных в условиях, когда применим оптимальный алгоритм. Полученные данные сравниваются с результатами, полученными оптимальным алгоритмом. В качестве основного критерия сравнения результатов используется значение суммарной стоимости перевозок (п. 2 формулы (2)). Дополнительным критерием качества может служить количество сообщений между агентами, отправленными в процессе моделирования.
Начальные входные данные генерируются следующим образом. Задается:
1) количество агентов-приемников;
2) максимальная потребность агентов-приемников в ресурсах FactoryMaxWeight;
3) количество агентов-источников;
4) максимальное количество ресурса агентов-источников TruckMaxWeight.
5) Агенты располагаются на поле размером 100х100.
Создается требуемое количество агентов-приемников, для каждого приемника положение по оси Х – случайное значение в диапазоне [1, 100]; положение по оси Y – случайное значение в диапазоне [1, 25]; потребность в ресурсах – случайное значение в диапазоне [TruckMaxWeight + 1, FactoryMaxWeight]. Также суммируется и запоминается общая потребность в ресурсах для всех агентов-приемников.
Создается требуемое количество агентов-источников, для каждого источника положение по оси Х – случайное значение в диапазоне [1, 100]; положение по оси Y – случайное значение в диапазоне [75, 100]; количество ресурса – случайное значение в диапазоне [1, TruckMaxWeight]. Суммируется общее количество ресурса для всех источников. Если оно не равно общей потребности в ресурсах для всех агентов-приемников, то значение количества ресурса для некоторых источников изменяется таким образом, чтобы общее количество было равно общей потребности в ресурсах.
Для работы оптимального алгоритма требуется расчет матрицы транспортных расходов, представляющей стоимость перевозки единицы ресурса каждым источником на каждый приемник. Стоимость пропорциональна расстоянию от каждого источника до каждого приемника.
Затем с использованием одних и тех же полученных начальных данных вычисляются суммарные затраты на перевозку оптимальным и предложенным алгоритмом. Значение суммарных затрат, полученных оптимальным алгоритмом, принимается за 100 %, после чего вычисляется превышение значения суммарных затрат, полученных предложенным алгоритмом.
На рисунке приведена схема автоматизированной системы сравнения результатов.
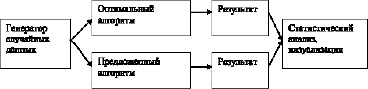
Схема автоматизированной системы сравнения результатов алгоритмов
Результаты вычислительного эксперимента
В качестве примера рассмотрим один из случайно созданных наборов входных данных. В нем 5 приемников и 20 источников. В табл. 1 и 2 приведены количества имеющихся и требуемых ресурсов и значения количества ресурса, передаваемые из источника на приемник; символом “;” отделено значение из матрицы стоимости перевозки по выбранному пути.
Таблица 1
Решение, полученное оптимальным алгоритмом
|
Приемник |
1 |
2 |
3 |
4 |
5 |
||
|
Потребность |
144 |
130 |
148 |
145 |
133 |
||
|
Источник |
Кол-во ресурса |
||||||
|
1 |
26 |
26;73 |
|||||
|
2 |
58 |
58;79 |
|||||
|
3 |
45 |
45;81 |
|||||
|
4 |
3 |
3;82 |
|||||
|
5 |
12 |
12;93 |
|||||
|
6 |
36 |
15;81 |
21;81 |
||||
|
7 |
18 |
12;99 |
6;84 |
||||
|
8 |
58 |
58;83 |
|||||
|
9 |
25 |
25;83 |
|||||
|
10 |
67 |
28;92 |
39;95 |
||||
|
11 |
32 |
32;80 |
|||||
|
12 |
16 |
16;85 |
|||||
|
13 |
20 |
20;81 |
|||||
|
14 |
44 |
44;74 |
|||||
|
15 |
54 |
54;91 |
|||||
|
16 |
12 |
12;93 |
|||||
|
17 |
50 |
50;91 |
|||||
|
18 |
52 |
52;86 |
|||||
|
19 |
34 |
34;62 |
|||||
|
20 |
38 |
38;66 |
|||||
Суммарная стоимость перевозок составляет 57729.
Таблица 2
Решение, полученное предложенным алгоритмом
|
Приемник |
1 |
2 |
3 |
4 |
5 |
||
|
Потребность |
144 |
130 |
148 |
145 |
133 |
||
|
Источник |
Кол-во ресурса |
||||||
|
1 |
26 |
26;90 |
|||||
|
2 |
58 |
58;79 |
|||||
|
3 |
45 |
19;81 |
26;95 |
||||
|
4 |
3 |
3;94 |
|||||
|
5 |
12 |
12;78 |
|||||
|
6 |
36 |
15;81 |
|||||
|
7 |
18 |
18;84 |
|||||
|
8 |
58 |
2;84 |
58;71 |
||||
|
9 |
25 |
25;97 |
|||||
|
10 |
67 |
67;98 |
|||||
|
11 |
32 |
32;80 |
|||||
|
12 |
16 |
16;80 |
|||||
|
13 |
20 |
14;86 |
6;81 |
||||
|
14 |
44 |
44;90 |
|||||
|
15 |
54 |
54;79 |
|||||
|
16 |
12 |
12;116 |
|||||
|
17 |
50 |
16;91 |
34;80 |
||||
|
18 |
52 |
52;86 |
|||||
|
19 |
34 |
34;80 |
|||||
|
20 |
38 |
38;83 |
|||||
Суммарная стоимость перевозок равна 59382.
Результат, полученный с помощью предложенного алгоритма, отличается от оптимального решения в рассмотренном случае на 3 %. Данный результат для установленных начальных данных свидетельствует о хорошем качестве получаемого решения.
Было проведено сравнение для трех серий (5 приемников и 20, 50 или 100 источников) по 100 случаев в каждом. Установлено, что результаты предложенного алгоритма – суммарная стоимость перевозки – отличаются от результатов оптимального алгоритма на 12–17 %.
Заключение
В работе рассмотрена распределительная задача с динамически изменяющимися условиями в процессе решения, к которой практически неприменимы ранее разработанные способы решения на основе динамического программирования. Предложено решение поставленной задачи с использованием мультиагентной системы на основе формирования коалиций агентов-источников, описан разработанный алгоритм. Этот подход применим к более широкому классу динамических задач. С целью оценки качества получаемых решений проведен вычислительный эксперимент для сравнения полученных результатов с результатами оптимального алгоритма на входных данных, к которым применим оптимальный алгоритм. Установлено, что результаты предложенного алгоритма для проведенной серии экспериментов отличаются от оптимальных на 12–17 %.



