Началом систематической разработки принципов пространственного проектирования лесовозных автомобильных дорог считают вторую половину прошлого столетия. К дорогам, как крупным инженерным сооружениям, были предъявлены архитектурные требования, коснувшись в первую очередь дорожных сооружений, мостов и придорожных территорий. В начале строительства использовались «Указания по архитектурно-ландшафтному проектированию автомобильных дорог», разработанные под руководством проф. В.Ф. Бабкова, проф. Е.М. Лобановым, доц. Н.П. Орнатским, инж. Ю.М. Белой, инж. М.Н. Финкельштейном и арх. Э.Л. Тетеровским [1].
Идеалом трасс по-прежнему оставалась длинная прямая, которая объясняется своеобразной психологической идеей проектировщиков, когда кривые радиусов, вынуждавшие снижать скорость и часто являющиеся причиной аварий, расценивались как нежелательные и опасные участки. Наоборот, редко встречаемые длинные прямые участки, которые автомобили могли проезжать с высокой скоростью, водителям идеальными для движения не считались. Считая кривые нежелательными, но неизбежными элементами трассы, проектировщики старались ограничить их количество и протяженность, назначая трассы, близкие к наименьшим допускаемым из условия обеспечения устойчивости лесовозного подвижного состава. Совмещение горизонтальных и вертикальных кривых малого радиуса также считалось обязательным, поскольку такие участки хуже соответствовали требованиям видимости. План и продольный профиль проектировали раздельно и независимо кроме полевого и камерального этапов.
Опыт первых лет строительства лесовозных автомобильных дорог способствовал выработке новых требований, их стали рассматривать как плавную пространственную кривую, которую нужно прокладывать взаимосвязанно в плане и в продольном профиле.
Цель работы заключается в обобщении исследований оценки зрительной плавности при проектировании лесовозных дорог, для построения математической модели оптимизации методов проектирования геометрических элементов лесовозных автомобильных дорог на стадии трассирования.
Материалы и методы исследования
Условия совмещения кривых плана и профиля для случаев, когда геометрический характер одинаков, можно найти в работах В.Ф. Бабкова, М. Госа и В. Веселы, И.В. Бегмы, А.П. Усова, В.К. Курьянова и др. авторов [1–3]. Эти рекомендации классически просты. Кривые в плане должны совмещаться с вертикальными вогнутыми закруглениями или немного ее перекрывать (первое условие зрительной плоскости). Выпуклые вертикальные кривые рекомендуется всегда перекрывать кривыми в плане.
В целях обеспечения ясности направления поворотов в плане, совмещенных с выпуклыми вертикальными кривыми, И.В. Бегма рекомендовал добиваться, чтобы пространственная (ось дороги, бровка) до границы видимости заметно отклонилась от предыдущего прямого направления дороги. Это можно сделать обеспеченным, если на перспективном изображении дороги, построенном в масштабе 1:100, отклонение кромок проезжей части от направлений касательных, проведенных из точек начала, на границе видимости не меньше 4 мм [4].
При проектировании дорог (особенно лесовозных) по многим причинам невозможно добиться точного совмещения элементов плана и продольного профиля. Вопросу о допустимых величинах смещения начал кривых (или вершин) в плане и профиле уделено большое внимание.
А.П. Усов [4] считает, что вершины кривых в продольном профиле и плане могут быть смещены до величины, соответствующей точности оценки водителями расстояния L. По его данным, в зависимости от скорости движения, могут быть допущены следующие величины смещений:
при V = 60 км/ч L = 40 м,
при V = 8 км/ч L = 55 м,
при V = 100 км/ч L = 70 м,
при V = 120 км/ч L = 90 м.
Особой проблемой обеспечения зрительной плавности и ясности дороги можно считать так называемые смещенные сочетания кривой плана и профиля.
Ряд отечественных ученых считают, что в случаях, когда конечное совмещение кривой в плане с вогнутой кривой в профиле осуществимо, повороты влево следует разбивать перед вогнутостью рельефа, а повороты вправо – за нею.
Согласно мнению Лоренца Г., допустимо смещение вертикальной и горизонтальных кривых на ¼ длины кривой в продольном профиле (обоснования этой рекомендации Лоренц не дал) [5].
Дайсинг считал, что m должно быть больше 5. В таком случае вогнутое закругление, расположенное в пределах кривых в плане, не воспринимается как «просадка» в перспективе [5].
По мнению П. Годена, соотношение m не должно быть меньше [6].
Наименьшее допустимое соотношение радиусов кривых для случаев идеально совмещенных кривых в плане и профиле в общем виде определили Х. Баккер и Г. Овердийкинк [4]. Это является основным условием зрительной ясности и выражается зависимостью
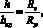(1)
bкр – расстояние до кромки дорожного полотна, м;
h – высота точки зрения над поверхностью дороги, м;
Rv, Rp – радиусы кривых в плане и продольном профиле.
Приведенный выше анализ касался простых случаев, когда кривая в продольном профиле более кривая в плане.
Вопросы образования зрительно ясных сложных сочетаний впервые затронул Г. Лоренц, рассматривая примеры некоторых часто встречаемых сложных линий. В частности, устройство обратных кривых в пределах лощин или проложение односторонней кривой в плане по волнистой поверхности рельефа [7].
Г. Лоренц отмечал, что эстетическим требованиям соответствуют участки дорог в тех случаях, когда точки перегиба трассы в плане совмещены с экспериментальными точками продольного профиля. Однако такое решение может быть широко применено, поскольку при этом не обеспечивается отвод воды с поверхности дорожного полотна в окрестностях точек перегиба кривых в плане, где поперечный уклон проезжей части iпоп = 0, а продольный уклон iпр = 0.
К обеспечению зрительной плавности элементарных кривых отражается следующие широко известные рекомендации:
- при проектировании трассы в плане и продольном профиле необходимо применять кривые больших радиусов;
- при малых углах поворота от 5 м до 1 м рекомендуется применить кривые больших радиусов – от 5000 м до 30000 м;
- непосредственно сопрягать между собой и с прямыми участками плана можно только кривые больших радиусов, порядка 1000–5000 м (В.Ф. Бабков [1]);
- в пересеченной местности трассу проложить в виде непрерывной извилистой линии.
Большинство рассмотренных рекомендаций являются эмпирическими. Особенно различны взгляды по вопросу о допустимой величине смещений начал (или вершин) кривых в плане и профиле.
В практике проектирования дорог встречаются случаи, когда запроектированные в строгом соответствии с приведенными эмпирическими правилами участки дорог оказывались неплавными. Здесь имеются в виду неудачи, получающиеся при точном совмещении начал клотоид в плане с началом новых кривых в профиле. Неплавными могут быть также и повороты дороги, которые образуют точно совмещенные круговые кривые в плане и профиле даже при больших их радиусах (например, левый поворот радиусом в плане Rp = 30000 м), имеющий горизонтальный продольный профиль.
Учитывая эти заключения, мы пришли к выводу, что эмпирические рекомендации нуждаются во всесторонней проверке и уточнении. Для оценки зрительной плавности поворотов необходимы, дополнительно к известным, новые условия, позволяющие учесть параметры пространственных линий и координаты расположения точек зрения перед их началом.
И.В. Бегма и Е.С. Томаревская [8, 9] предлагали в качестве количественного показателя зрительной плавности использовать величину f, определенную на перспективном изображении криволинейного участка дороги (на плоскости х = 1 м), между кромкой проезжей части и точкой пересечения касательных, проведенных из точек начала и конца кривой. Критерием плавности поворота авторы предлагали величину f ≥ 10 мм для кривых в плане и 4 мм для вогнутых закруглений в продольном профиле. Критерием перелома линий в плане f < 4 мм.
Использование упомянутых критериев было рекомендовано для прямых в плане участков, имеющихся закругления в продольном профиле, и плоских участков дороги с кривой в плане. Недостатком описанного метода является то, что его нельзя преобразовать для оценки плавности пространственных кривых, для точки зрительной плавности и ясности сложных участков, кривых в плане и профиле.
Ряд отечественных авторов предлагают принять в качестве геометрического показателя зрительной плавности степень изменения величины перспективной проекции f отрезка h дуги криволинейной трассы в процессе его перемещения по кривой. Степень увеличения отрезка h будет отражать производная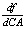 
. dCA – бесконечно малая длина дуги пространственной линии.
Величину В.В. Сафонов предлагает принять за критерий зрительной плавности [10]. В результате вычислений должны быть построены графики, изображающие для каждого положения центра проецирования кривую зрительной плавности. В результате вычислений должны быть построены графики, изображающие для каждого положения центра проецирования кривую зрительной плавности. Каждой точке графика соответствует определенная точка трассы. В дальнейшем это предположение автор не реализовал и поэтому судить о его удачности сомнительно.
Имеется принципиальное возражение – метод В.В. Сафонова не дает возможности контролировать зрительную ясность [10]. Как доказывается далее, необоснованными являются также и выводы В.В. Сафонова, что радиус кривизны не может быть характеристикой зрительной плавности.
В. Пфейл предлагал для проверки зрительной ясности использовать количественный критерий [11]:
К =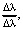 
(2)
Δλ – изменение угла перспективного изображения пространственной кривой, соответствующее единице пути;
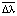– изменение угла перспективе на единицу горизонтальной проекции пространственной кривой.
Показатель К < 1, по мнению В. Пфейла, характеризует хорошее положение трассы в пространстве. Если К > 1, то это показывает, что кривые зрительно воспринимаются пологими, а это может привести к превышению безопасности для данной кривой скорости.
К < 0 указывает на то, что направление изогнутости линий в перспективе не соответствует ее направлению в плане. Например, левый поворот воспринимается как правый.
Как видно, предложенный В. Пфейлом математический аппарат позволяет проверить лишь зрительную ясность пространственных линий. Являясь зрительно ясными, кромки проезжей части или другими на дорожном полотне могут быть неплавными. Однако В. Пфейл не приводит дополнительных критериев, позволяющих проверить также и проверку плавности участков дорог.
Следует отметить, что показатель «хорошей трассы» К > 1 соответствует случаям совмещения выпуклых кривых в продольном профиле с кривыми в плане. Размещение кривых, особенно на малых участках, на вогнутых участках продольного профиля В. Пфейл считает нежелательными, чтобы повышенная степень их зрительной плавности не стала причиной превышения водителями безопасной скорости. Частные происшествия на кривых малых радиусов, совмещенными вогнутыми вертикальными кривыми отмечаются в статистике ГИБДД [5].
А.А. Кузиков [12] сделал попытку выразить связь между практическими показателями видимой картины дороги и допускаемой при ее восприятии скоростью движения. В качестве геометрических показателей избраны экстремальная кривизна Кэкс и ее …. Sэкс, которые, по его мнению, наиболее полно характеризуют видимую картину трассы. Эти геометрические показатели определяются для точек оси дороги (а не для кромок проезжей части или бровок дорожного полотна) при скачкообразном перемещении точки зрения также по оси дороги. Проверяемая на плавность линия – ось дороги – центрально проецируется на единичную сферическую поверхность.
В качестве комплексного показателя зрительной плавности Кузиков предлагал использовать предел психологически комбинированной скорости Vпс км/час, который определяется с геометрических показателей Кэкс Sэкс. Результатом выгнутой является эпюра Vпр.
Кинематически понимаемую зрительную плавность указанный …. считает обеспеченной, если получаемая для трассы эпюра не имеет резких колебаний и не опускается ниже уровня расчетной скорости. К сожалению, метод не обеспечивает надежности обратной связи. Поэтому получение желаемой эпюры считается постепенным приближением.
При оценке метода замечены следующие его недостатки. Исследования, проведенные нами в последние годы, показали, что более полной геометрической характеристики зрительной плавности, кроме наибольшей видимой кривизны Кн, необходимо учитывать наибольшую скорость ее изменения К'н, а также длину кривой.
В связи с малой изученностью визуально-рефлекторной связи учитывается лишь два из возможных показателя при определении Vпс, надежность предлагаемого метода не представляется достаточной.
Следует также отметить, что невозможно раскрыть зрительные перспективы дороги, аналитически исследуя лишь одну из образующих линий, т.е. ось дороги при перемещении точки зрения оси.
Нельзя согласиться и с отрицательным отношением А.А. Кузикова полезности для зрительного анализа применявшихся до сих пор методов. Долголетний опыт пространственного проектирования в нашей стране и за рубежом показал, что использование активных изображений и моделей способствовало созданию новых участков дорог по ландшафтно-архитектурной и транспортной эксплуатационной оценкам. Основной недостаток этих методов – трудоемкость, а не непригодность для зрительного анализа [11].
После дальнейшего усовершенствования такой метод окажется в первую очередь при проектировании пространственных изображений, имеющих малые радиусы в плане. К такому заключению приходят некоторые исследователи, в том числе Е.М. Лобанова [5], которая установила повышенную степень зональной напряженности при проезде кривых, имеющих радиусы менее 800 м. Влияние кривых больших радиусов на режимах движения практически не отражалось. Поэтому можно полагать, что показатель Vпс, предложенный А.А. Кузиковым [6], в первую очередь может иметь значение при кинематической оценке критериев, на которых происходит снижение скорости транспортного полотна.
Как видно из обзора, математический метод В. Пфейла [12] приспособлен для контроля зрительной ясности, а методы В.В. Сафонова и А.А. Кузикова [8, 12] приспособлены для проверки зрительной плавности. Надежность одновременного контроля плавности и ясности рассматриваемых методов не обеспечивает, что является их недостатком.
Заключение
До сих пор методы пространственного проектирования дорог были эмпирическими. Методы проектирования дорог в увязке с ландшафтом еще нуждаются в интенсивной разработке. Изучение опыта пространственного проектирования и главным образом обоснованности количественных рекомендаций показывают, что нужны более эффективные средства исследования этой темы. Для оценки плавности дороги нужны математические показатели и объективные критерии. До тех пор, пока сами понятия «плавность дороги» и «реальная ясность» недостаточно определены с математической точки зрения, не могут быть предложены и их количественные характеристики.
Учитывая вышесказанное, в дальнейшем необходимо:
1. Исследовать количественные показатели кривизны кривых, характеризующие плавность и ясность параллельных проекций пространственных и плоских кривых.
2. Разработать аналитические методы оценки зрительной плавности и ясности траекторий движения глаз водителя лесовозного автомобиля.
3. Усовершенствовать методику пространственного проектирования лесовозных автомобильных дорог на топографических картах.
4. Провести экономическую оценку эффективности применения методики пространственного проектирования лесовозных автомобильных дорог.