Задача прогнозирования временных рядов является основой для мониторинга состояния сложных технических систем на примере малых космических аппаратов (КА). Она может быть решена на примере малых летательных аппаратов [1]. Такая задача с использованием байесовского подхода была решена, например, в работе [2], в которой предлагается алгоритм определения и прогнозирования уровня опасности на основе данных телеметрии, а также проведены экспериментальные исследования. В данной работе основной упор сделан на использование искусственной нейронной сети (ИНС) в качестве инструмента для прогнозирования состояния сложных технических систем на примере КА. Для корректного сравнения результатов работы двух подходов обучение ИНС проводилось на тех же данных, что и в работе [3].
Исследование посвящено использованию ИНС в качестве инструмента для прогнозирования состояния сложных технических систем на примере КА. Совместно с регрессионной моделью на основе ИНС прямого распространения контролю технического состояния КА.
Материалы и методы исследования
1. Задача прогнозирования состояния подсистем КА
В соответствии с сформулированной целью позаимствуем обозначения из работы [2] и выполним постановку задачи в новой интерпретации с расчетом на использование ИНС.
Пусть
1) x(t) – показания датчиков в определенный момент времени t;
2) x* – значение, превышение которого считается аномальной ситуацией;
3) Vi (i = 1, …, n) – состояние системы, для которой осуществляется прогнозирование;
4) T – интервал времени для расчетов появления аномалий;
5) d1, d2, …, dm – уровни опасности (УО);
6) p* – критическое значение выхода нейронной сети, интерпретируемое как вероятность аварийного состояния;
7) dt – шаг дискретизации времени;
8) x'(t) – рассчитанная производная x(t), которую заменяем на разности между соседними значениями временного ряда при постоянном интервале времени, принимаемом за единицу;
9) Δt1 < Δt2 < … < Δtm – прогнозные границы (интервалы времени), которые соответствуют уровню опасностей.
Рассмотрим подсистему космического аппарата, которая передает значения x(t) каждые dt минут. Полученные значения можно применить для расчета вектора показателей (x(t), x’(t)), которые определяют состояние системы Vi (i = 1, …, n). Необходимо дать правдоподобный прогноз, что при текущей истории изменений x(t) наступит аварийное состояние в определенный промежуток времени, обозначаемый как Δt. Очевидно, что чем выше прогнозная граница, тем выше вероятность того, что аварийная ситуация произойдет хотя бы один раз за этот период. Зададим p* и выделим прогнозные границы. При расчете вероятности P(x(t + Δt) > x*) > p* текущее состояние будет опаснее, если значение Δt меньше. Произвольно определим граничные значения Δt, которые разделяют разные уровни опасности. Если j = min (P (∃ τ ∈ [t, t + Δtj]: x(t + τ) > x*) > p*), состояние системы соответствует j-му уровню опасности. При достижении которой x(t) превышает пороговое значение x*, каждому состоянию системы присваивается уровень угрозы и граница прогноза. Уровни угроз классифицируются в соответствии со значением Δtj – чем ниже значение Δtj, тем выше уровень. Выполнение задачи прогнозирования превышения допустимого предела заключается в вычислении уровня угрозы текущего состояния по алгоритму.
Расчет УО требует обучения искусственной нейронной сети. Зададим определенные параметры:
− пороговое значение x*;
− уровни опасности d1, d2, … dm;
− прогнозные границы Δt1 < Δt2 < … < Δtm, соответствующие уровням опасности;
− интервалы времени dt и T;
− критическое значение вероятности аварийной ситуации p*.
После определения начальных параметров проводится обучение ИНС для алгоритма анализа данных потока.
2. Искусственная нейронная сеть для контроля КА
Для контроля состояния сложных технических систем на примере использовалась ИНС прямого распространения вместе с регрессионной моделью, создается отдельная ИНС для каждой подсистемы КА. Нейросетевой комплекс обнаруживает угрозу с точностью до блока, что позволяет сократить время реабилитации технического объекта, комплекс показан на рис. 1 [4].
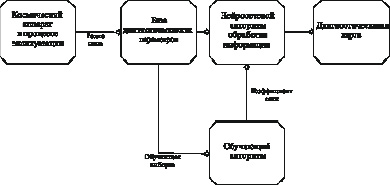
Рис. 1. Контроль состояния космического аппарата
Для обучения ИНС [5] использовались сохраненные потоки и данные. Обучающая выборка подбирается отдельно для каждой сети комплекса. Совместное использование ИНС и регрессионных технологий значительно улучшает контроль систем КА, что продлевает жизненный цикл космических аппаратов.
Рассмотрим задачу контроля на примере бортовой системы электроснабжения (СЭ) КА. Для обеспечения правильного энергетического состояния КА необходимо принять как технические, так и организационные меры для обеспечения функциональности и отказоустойчивости бортовых систем. Система ЭС КА обеспечивает питание всех подсистем аппарата, выход ее из строя приведет к отказу всего технического объекта. Предложено решение задачи контроля систем электроснабжения с помощью набора ИНС, которые объединены в единую схему, представленную на рис. 2 [6, 7]. Расчет величины QАБ(t) основан на определении временного интервала, в течение которого мощность и нагрузка остаются неизменными. Массив величин разностей является основой для построения системы ИНС, позволяющей определять энергетическое состояние. Контролирующий комплекс состоит из пяти ИНС, в котором каждая реализует модель функционирования соответствующего компонента СЭ: солнечной батареи (СБ); стабилизатора напряжения (СН); аккумуляторной батареи (АБ); разрядного устройства (РУ); зарядного устройства (ЗУ). Нейронная сеть работает совместно с блоком вычисления освещенности солнечной батареи, блоком задач и блоком логического управления коммутационно-распределительных устройств.
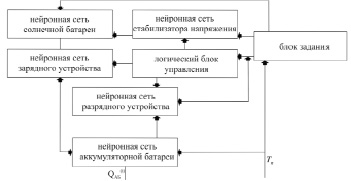
Рис. 2. Структура ИНС для прогнозирования энергетического состояния КА
В процессе работы ИНС обучаются на основе текущих измерений параметров состояния соответствующих подсистем, токов I и напряжений U. При прогнозировании энергетического состояния нейронные сети используются для расчета напряжений на входах/выходах компонентов бортовой СЭ, а также для расчета состояния заряда аккумуляторных батарей.
Результаты исследования и их обсуждение
Экспериментальные исследования контроля на основе нейронной сети по данным телеметрии
Сеть прямого распространения со скрытым слоем применялась для обработки данных телеметрических данных КА. Архитектура сети: входной слой – 5 нейронов, выходной слой – 5 нейронов и скрытый слой – 500 нейронов. Для экспериментов использовался поток телеметрических данных космического аппарата «Юбилейный» [8]. Каждую минуту аппарат передает данные о токе, напряжении, температуре и других параметрах. Фрагмент данных телеметрии КА представлен в табл. 1.
Таблица 1
Поток данных телеметрии с трех датчиков КА
|
Время |
Значения с датчиков КА |
||
|
Bort_V |
Bort_A |
Sun_V |
|
|
12:09:44 |
14.7 |
0.15 |
0.11 |
|
12:10:44 |
14.7 |
0.18 |
0.11 |
|
12:11:44 |
14.6 |
0.18 |
0.28 |
|
12:12:44 |
14.5 |
0.18 |
0.95 |
|
12:13:44 |
13.10 |
0.15 |
14.20 |
На примере датчика Bort_V рассмотрим фрагмент потока данных телеметрии, который показан на рис. 3. Пороговое значение x* для этого датчика установлено равным 14,7. Значения выше этого порога считаются аномальными.
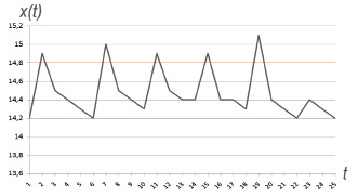
Рис. 3. Данные телеметрии КА
Для реализации подхода требуется задать некоторые параметры: три прогнозные границы (в минутах): уровни опасности, заданные в соответствии с прогнозными границами: d1 = 3 (высокий УО), d2 = 2 (средний УО), d3 = 1 (низкий УО); t1 = 20, t2 = 30, t3 = 50; dt = 1; пороговое значение x* = 14,7; T = 3000, тогда N = T / dt = 3000.
Для прогнозирования возникновения аварийных ситуаций датчиковой аппаратуры КА использовалась динамически переобучающаяся ИНС прямого распространения. ИНС имеет выходов (количество выходных нейронов – это способность нейронной сети предсказывать поведение оборудования на p шагов вперед) и входов (размер скользящего окна). Численность скрытых нейронов и слоев определяют настройки. Нейросеть с четырьмя слоями и больше показала результаты получше.
С существующими наборами тестовых данных представленный метод оказался лучшим. За счет плавного изменения телеметрических данных КА точность прогноза гарантируется. При резком изменении телеметрических данных обнаруживается неисправность датчика, так как за счет дополнительного обучения ИНС данные с помехами заносятся в ИНС.
С использованием алгоритма RPROP [9] нейронная сеть обучается. В качестве функции активации для каждого из нейронов ИНС был выбран гиперболический тангенс. Сеть прямого распространения была дополнена слоем сети векторного квантования. Количество нейронов в сети векторного квантования соответствует количеству классов, определенных в обучающей выборке. Формирование обучающей выборки для сети векторного квантования происходит в автоматическом режиме по разработанному алгоритму.
Для тестирования возможностей нейронной сети предложен следующий алго- ритм:
1) выбираем случайный вектор из исходной обучающей выборки;
2) выбираем случайную позицию в векторе значений;
3) определяем данную позицию как неизвестное значений, обнуляя ее;
4) передаем модифицированный вектор на вход ИНС и восстанавливая неизвестное значение;
5) оцениваем отклонение восстановленного значения от значения, представленного в векторе, выбранном на первом шаге алгоритма.
Тестирование проводилось на показаниях группы из пяти датчиков: «Sun, A» (ток солнца), «Sun, V» (напряжение солнца),»Sp3, A» (I Сп3), «Sp2, A» (I Сп2) и «Sp1, A» (I Сп1). Было проведено пять независимых тестов, каждый из которых обучил ИНС и протестировал тысячу векторов с внесенными ошибками. Фрагмент результатов тестирования приведен в табл. 2 и на рис. 4.
Таблица 2
Фрагмент результата работы алгоритма
|
t |
dj |
x(t) |
|
1 |
0 |
14.3 |
|
2 |
3 |
14.8 |
|
3 |
3 |
14.4 |
|
4 |
3 |
14.5 |
|
5 |
3 |
14.4 |
|
6 |
3 |
14.3 |
|
7 |
3 |
15 |
|
8 |
3 |
14.5 |
|
9 |
3 |
14.3 |
|
10 |
3 |
14.4 |
|
11 |
1 |
14.8 |
|
12 |
3 |
14.4 |
|
13 |
3 |
14.5 |
|
14 |
2 |
14.3 |
|
15 |
1 |
14.8 |
|
16 |
3 |
14.5 |
|
17 |
2 |
14.5 |
|
18 |
3 |
14.4 |
|
19 |
0 |
15.2 |
|
20 |
0 |
14.5 |
|
21 |
3 |
14.4 |
|
22 |
3 |
14.3 |
|
23 |
0 |
14.5 |
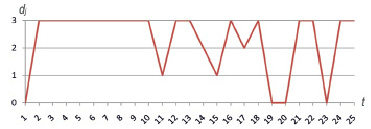
Рис. 4. Уровни опасности для датчика Bort_V
При x(3) = 14,4 уровень риска высок, т.е. в течение 20 мин x(t) превышает пороговое значение x* = 14,7. Для x (3) = 14,4 прогноз подтвердился через 4, 8, 12 и т.д. мин: х (7) = 15, х (11) = 14,8, х (15) = 14,8. Точность прогноза составляет около 86 %.
Заключение
В настоящей работе предложен и исследован метод нейросетевого прогнозирования поведения аномалий в потоках данных с космических подсистем. Его сравнение с байесовским подходом [2] оказывает идентичность получаемых результатов при относительной простоте алгоритма настройки и возможности распараллеливания задачи на несколько прогнозных интервалов. Отличаясь простотой реализации, нейросетевой метод уместен при его использовании как в наземных, так и в бортовых системах контроля наличия сбоев в телеметрии.
Исследование выполнено в рамках госбюджетной темы «Архитектура, системное, инструментальное и прикладное программное обеспечение, методы анализа и верификации информационно-вычислительных комплексов и сетей новых поколений». Номер гос. регистрации АААА-А19-119020690043-9.



