Выделяют три основные группы методов частиц: частица-частица (лагранжевы методы частиц), частица-сетка (эйлеров подход) и частица-частица – частица-сетка (смешанные методы частиц) [1, 2]. Большинство вышеприведенных приложений методов частиц носят научно-исследовательский характер [2, 3]. Однако они практически не имеют приложений в технике, но при соответствующей адаптации могут быть успешно применены в моделировании процессов электролиза, газоочистки, движения газа при трубопроводном проветривании [4–6].
Целью проведения данного исследования является анализ существующих методов моделирования потоков частиц, а также анализ применимости методов для моделирования потоков заряженных частиц в электростатическом поле электродов пластинчатого электрофильтра очистки отходящих газов ЭГАВ 1-40-9-6-3 и создать математическую модель движения заряженных частиц. Результаты моделирования должны согласоваться с процессом очистки отходящих газов в электрофильтре.
Моделирование
Пусть электроды расположены на границе трехмерной прямоугольной области, то есть параллелепипеда. Без ограничения общности можно рассматривать только случай, когда электроды расположены на гранях. Будем считать при этом, что заряды на гранях параллелепипеда известны и распределены равномерно. Если грань не является поверхностью электрода, заряд полагается равным нулю. При таких условиях характеристики электростатического поля (потенциал, напряженность), создаваемого между электродами внутри параллелепипеда, зависят только от переменных x и y. Таким образом мы можем моделировать процесс только в плоскости XOY.
Рассмотрим прямоугольник D в плоскости XOY, высота которого равна l1, а длина основания – 2d (рис. 1). Будем использовать для границ прямоугольника те же обозначения, что и для граней параллелепипеда, к которым они принадлежат. Обозначим через qi заряд на поверхности Pi.
.
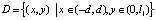Граничные условия имеют вид
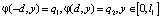, (1)
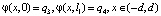. (2)
Для расчета потенциала необходимо, чтобы выполнялись условия согласования
,
,
,
.
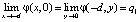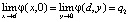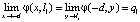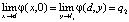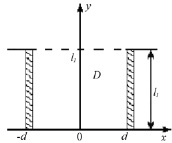
Рис. 1. Область D
Этого можно добиться, заменив условия (2) приближенными условиями
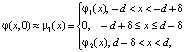(3)
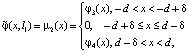(4)
где δ > 0 – достаточно малое действительное число, φi(x), i = 1,2,3,4 – дважды непрерывно дифференцируемые функции, φ1(-d) = φ3(-d) = q1, φ2(d) = φ4(d) = q2.
Пусть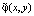 
– решение краевой задачи (1), (3), (4). Наиболее удобно взять φ1 и φ2 в виде кубических сплайнов:
.
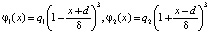При таком выборе φ1(x) и φ2(x)
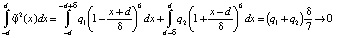при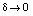 
.
Это доказывает, что функция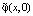 
аппроксимирует граничные данные (2).
Из уравнения Лапласа следует, что
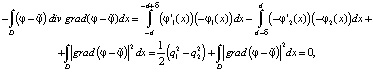
откуда
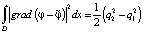. (5)
Используя неравенство Гельдера
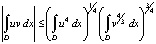
и тот факт, что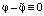 
в области 
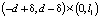как решение задачи Дирихле для уравнения
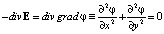(6)
с однородными граничными условиями, из (5) получаем
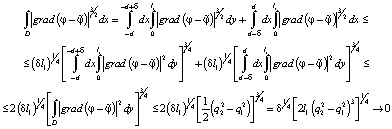
при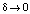 
, откуда следует, что 
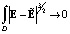при 
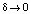, где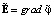 
. Таким образом, 
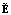аппроксимирует E.
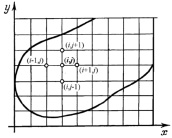
Рис. 2. Пятиточечный шаблон
Задачу (1) и (3) будем решать численно, используя разностный метод (метод сеток) [4, 5]. Для этого построим разностную схему на пятиточечном шаблоне (рис. 2). Зададим сетку в области D с шагом hx по x и hy по y. Положим
.
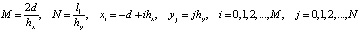Вторые производные в уравнении (6) заменим симметричными разделенными разностями:
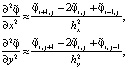
где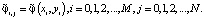 
Разностная схема имеет вид
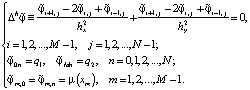(7)
Данная разностная схема устойчива. Приближенное решение сеточной задачи (7) сходится к точному решению задачи (1), (3) пр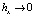и 
и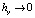 
, причем порядок скорости сходимости совпадает с порядком аппроксимации 
.
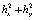Пусть в момент t1 заряженная частица находится в точке с координатами (x1, y1) и имеет скорость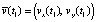 
. Уравнение движения частицы вдоль оси X имеет вид
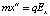. (8)
Так как q и E постоянны, ускорение частицы вдоль оси X равно
,
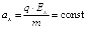то есть движение вдоль X равноускоренное. Найдем скорость vx из (8):
.
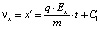Постоянная интегрирования C1 определяется из начального условия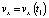 
при t = t1, что дает для C1 значение, равное нулю. Последнее выражение перепишем следующим образом:
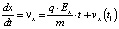, (9)
отсюда
.
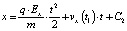Из начального условия x(0) = x1 следует, что C2 = x1. Поэтому
.
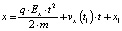Перейдем к решению уравнения движения вдоль оси Y:
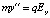. (10)
Так как q и Ey постоянны, ускорение частицы вдоль оси y равно
.
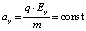Таким образом, движение вдоль Y также равноускоренное:
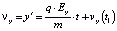, (11)
отсюда
.
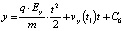Из начального условия y(0) = 0 получаем для C6 значение, равное y1. Поэтому:
.
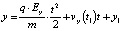Таким образом, система кинематических уравнений движения частицы в электростатическом поле имеет вид
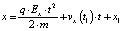, (12)
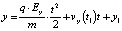. (13)
В частности, при параллельном расположении электродов напряженность поля остается постоянной во всей области, причем Ey = 0. Поэтому в силу начальных условий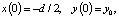 
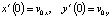уравнения (12), (13) принимают вид
,
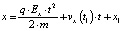y = y0.
Уравнения (12), (13) параметрически задают прямую y = y0 на плоскости xOy, представляющую траекторию движения заряженной частицы в пространстве между электродами [7–9].
На рис. 3 представлены результаты численного эксперимента в виде компьютерного моделирования движения заряженных частиц пыли в электрофильтре ЭГАВ 1-40-9-6-3 [7–9], где слева – поток заряженных частиц пыли в электрофильтре, справа – потенциалы коронирующего (синий) и осадительного (красный) электродов, в специально разработанной для этого программе [10].
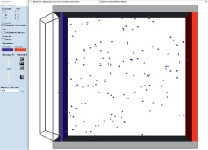
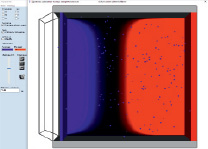
Рис. 3. Моделирование потока пыли при работе электрофильтра ЭГАВ 1-40-9-6-3. Данный тип электрофильтров характерен для большинства крупных промышленных предприятий Российской Федерации и стран СНГ [11, 12]
Заключение
Для моделирования потока частиц пыли был разработан метод частиц, относящийся к смешанным алгоритмам, в котором каждый участок траектории движения частицы рассматривается как сплайн и находится путем дискретизации напряженности и интегрирования уравнений движения в электростатическом поле [7–9]. Численный эксперимент по компьютерному моделированию потока частиц пыли в электрофильтре был проведен для электрофильтра ЭГАВ 1-40-9-6-3, тип которого характерен для большинства крупных промышленных предприятий Российской Федерации и стран СНГ [10, 11] и делался в специально разработанной для этого программе [12]. Результаты моделирования согласуются с процессами, происходящими в электрофильтре во время его работы.