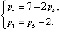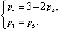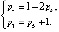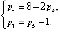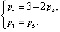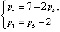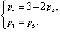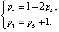Темпы развития металлургической и смежных с ней отраслей промышленности постоянно требуют усовершенствования конструкций дробильного оборудования [1–4]. Внедрение новой техники, а также повышение её эффективности позволяет решать ряд важных задач, таких как снижение себестоимости оборудования, повышение качества технологических процессов, увеличение рентабельности производства. Все процессы измельчения характеризуются высокой энергоемкостью, поэтому особое внимание уделяется энергетическим затратам, которые при проектировании учитываются только через процесс дробления материала [5–8]. В результате мощность электродвигателя, как правило, выбирают на 30–50 % больше мощности, получаемой при расчете по существующим формулам [1]. Существенно уменьшить расход энергии дробильных машин можно путем создания самоустанавливающихся структур дробильных машин нового поколения.
Известно, что используемые в дробилках подшипники для соединения между собой деталей (звеньев) не могут обеспечить их самоустановку, в результате наблюдается перегрузка всех звеньев, вызывающая повышенный износ соприкасающихся поверхностей деталей и заклинивание звеньев, что приводит к полной остановке процесса дробления. В работе поставлена задача создания самоустанавливающейся новой структуры дробильной восьмизвенной машины, по созданной методике, разработанной в научной школе Сибирского государственного индустриального университета.
Материалы и методы исследования
Исследование основано на использовании: известных структурных формул подвижности В.В. Добровольского – И.И. Артоболевского, основных положений структурного анализа и синтеза академика И.И. Артоболевского и профессоров В.В. Добровольского, Г.Г. Баранова, Л.В. Ассура, универсальной структурной системы (УСС) профессора Л.Т. Дворникова и принципов определения и исключения избыточных связей в механизмах профессоров Н.И. Колчина, Л.Н. Решетова.
Результаты исследования и их обсуждение
Кинематическая цепь щековой дробилки, защищенной патентом [9], показана на рис. 1, она представлена начальным звеном 1, соединенным со стойкой О1, закон движения которого задается, и двумя группами Ассура – диадой АВО2 и четырехзвенной группой CEFDGO3.
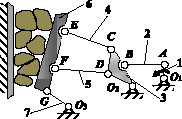
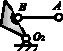
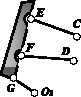
Рис. 1. Структура щековой дробилки и её структурные элементы
В структуре щековой дробилки семь подвижных звеньев (n = 7), которые соединены между собой десятью одноподвижными кинематическими парами (р = 10), т.е. парами пятого класса – р5. Такие структуры механизмов по классификации И.И. Артоболевского [10] и других исследователей относятся к механизмам третьего семейства (m = 3).
Создать плоский механизм при дефиците подвижности в шарнирах, обеспечив строгую параллельность всех его геометрических осей, нельзя, так как невозможно изготовить звенья, с размерами в точном соответствии с расчетными значениями, следовательно, и собрать механизм окажется невозможно без принуждения. Реально все оси шарниров будут попарно пересекаться, и тогда вся система после сборки перестанет быть плоской, её звенья будут дополнительно напряжены изгибающими моментами. Он станет избыточным по связям. Число таких связей определяется формулой
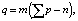(1)
где m – число общих связей, накладываемых на механизм в целом, р – число кинематических пар (соединений), n – число подвижных звеньев.
Если наличие и число избыточных связей в механизмах определять исходя из зависимости (1), то, казалось бы, очевидным является вывод о том, что при m = 0 все создаваемые цепи будут безызбыточными. Однако это не так. Условие m = 0 всего лишь определяет, что такие системы описываются уравнением подвижности А.П. Малышева, и это условие является необходимым, но не достаточным. Достаточным оно будет лишь в том случае, когда создаются одноконтурные кинематические цепи [11], т.е. цепи с двумя выходами на стойку, например шарнирный четырехзвенник.
Число избыточных связей по (1) в рассматриваемой структуре механизма дробилки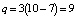 
. Используя преимущества плоской и пространственной структур, а именно, то, что механизмы третьего семейства имеют наименьшее число звеньев по сравнению с пространственными, но являются избыточными по связям, а пространственные являются самоустанавливающимися, т.е. q = 0, но состоят из большего числа подвижных звеньев, переведем структуру плоского восьмизвенного механизма дробления в пространственную, без увеличения числа звеньев.
Рассматриваемая структура механизма не является одноконтурной, и при решении задачи исключения избыточных связей в более сложных цепях [11] условие (1) оказывается недостаточным, так как необходимо обеспечить отсутствие избыточных связей не только в механизме в целом, но и в каждой группе Ассура, входящей в его состав. Применим для решения поставленной задачи универсальный метод исключения избыточных связей с адресной заменой шарниров на кинематические пары более высоких классов [11]. Метод содержит шесть этапов решения. На первом этапе, при заданном общем числе подвижных звеньев и подвижности цепи, определяются числа всех кинематических пар по системе (2) от первого (р1) до пятого (р5) классов, из которых должна состоять без избыточных связей в целом исследуемая кинематическая цепь. Это решение является общим структурным решением кинематической цепи внутри нулевого семейства (m = 0):
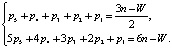(2)
Если при решении использовать кинематические пары р3, р4 и р5, как наиболее простые в изготовлении, то система (2) примет вид
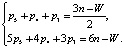(2.1)
Второй этап предусматривает декомпозицию кинематической цепи на замкнутые контуры и фрагменты. Количество декомпозиций определяется формулой Гохмана r = (p – n), где r – число независимых замкнутых контуров.
В третьем этапе находятся числа используемых кинематических пар в каждом выделенном замкнутом контуре и фрагментах всех декомпозиций. В четвертом определяются комплексные решения выделенного замкнутого контура и фрагментов. В пятом этапе сравниваются комплексные решения декомпозиций с общими решениями внутри нулевого семейства с целью выявления совпадающих. Если совпадающими будут несколько вариантов решений, то предпочтение может быть отдано тому, в котором будут присутствовать наиболее простые в реализации кинематические пары.
В последнем (шестом) этапе, основываясь на выбранном варианте решения, составляются адресные уравнения, в которых слева записываются алгебраические суммы буквенных обозначений кинематических пар, входящих в состав контура или фрагмента, а справа – соответствующие им решения. Количество адресных уравнений определяется общим решением внутри нулевого семейства механизма и уравнениями частных решений декомпозиций, а именно, выделенных контуров и фрагментов.
Если решить систему уравнений (2.1) относительно количества кинематических пар третьего и четвертого классов, то получим
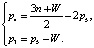(3)
Рассматриваемый механизм содержит n = 7, p5 = 10 и подвижность его W = 1, система (3) в этом случае примет вид
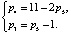(3.1)
Эта система имеет пять целочисленных положительных вариантов решений, каждый из которых формально в целом удовлетворяет условию создания механизма без избыточных связей
1. p5 = 5, p4 = 1, p3 = 4.
2. p5 = 4, p4 = 3, p3 = 3.
3. p5 = 3, p4 = 5, p3 = 2.
4. p5 = 2, p4 = 7, p3 = 1.
5. p5 = 1, p4 = 9, p3 = 0. (4)
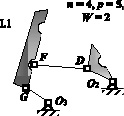
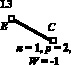
Для устранения избыточных связей не только в механизме, но и в каждой группе Ассура рассматриваемого механизма, проведем его декомпозицию на замкнутые контуры и дополняющие эти контуры фрагменты. Обратим внимание на то, что декомпозиция механизма на замкнутые контуры и фрагменты является операцией вполне очевидной, но ответственной, и для различных механизмов требует часто вдумчивого подхода. На рис. 2 приведена декомпозиция исследуемого механизма, в котором кинематические пары показаны как виртуальные, которые подлежат идентификации.
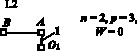
Первая декомпозиция
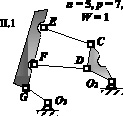
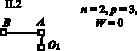
Вторая декомпозиция
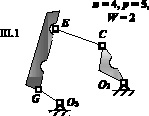
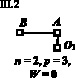
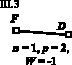
Третья декомпозиция
Рис. 2. Декомпозиции механизма на контуры и фрагменты
Для идентификации пар обозначим их соответствующими буквами (рис. 2) и в каждой декомпозиции рядом с замкнутым контуром и дополняющими его фрагментами приведем параметры чисел звеньев, кинематических пар, а также соответствующую им подвижность. Таким образом, задача сводится к тому, чтобы найти десять решений, определяющих положение пар рk по адресам О1, А, B, C, D, E, F, G, О2, О3, т.е. рА, рB, рC, рD, рE, рF, рG, рО1, рО2, рО3. Запишем в таблице соответствующие системы уравнений и их решения по (3), а также комплексные решения для каждой декомпозиции. Анализ приведенных в таблице решений показывает, что в первой декомпозиции комплексных решений два.
Результаты решений декомпозиций механизма (рис. 2) по контурам и фрагментам
|
Декомпо – зиции |
Системы уравнений (3) |
Варианты решений систем уравнений (3) |
Комплексные решения декомпозиций |
|
I.1 |
|
1.1 p5 = 3, p4 = 1, p3 = 1, 1.2 p5 = 2, p4 = 3, p3 = 0. |
p5 = 4, p4 = 3, p3 = 3, p5 = 3, p4 = 5, p3 = 2. |
|
I.2 |
|
1.3 p5 = 1, p4 = 1, p3 = 1. |
|
|
I.3 |
|
1.4 p5 = 0, p4 = 1, p3 = 1. |
|
|
II.1 |
|
2.1 p5 = 3, p4 = 2, p3 = 2, 2.2 p5 = 2, p4 = 4, p3 = 1, 2.3 p5 = 1, p4 = 6, p3 = 0. |
p5 = 4, p4 = 3, p3 = 3, p5 = 3, p4 = 5, p3 = 2, p5 = 2, p4 = 7, p3 = 1. |
|
II.2 |
|
2.4 p5 = 1, p4 = 1, p3 = 1. |
|
|
III.1 |
|
3.1 p5 = 3, p4 = 1, p3 = 1, 3.2 p5 = 2, p4 = 3, p3 = 0. |
p5 = 4, p4 = 3, p3 = 3, p5 = 3, p4 = 5, p3 = 2. |
|
III.2 |
|
3.3 p5 = 1, p4 = 1, p3 = 1. |
|
|
III.3 |
|
3.4 p5 = 0, p4 = 1, p3 = 1. |
Первый вариант комплексного решения p5 = 4, p4 = 3, p3 = 3 получился в результате сложения одинаковых кинематических пар решений 1.1, 1.3 и 1.4, т.е. (р5 = 3 + 1 + 0 = 4; р4 = 1 + 1 + 1 = 3 и р3 = 1 + 1 + 1 = 3). Второй вариант решения p5 = 3, p4 = 5, p3 = 2 получается сложением решений контура и фрагментов 1.2, 1.3 и 1.4, т.е. (р5 = 2 + 1 + 0 = 3; р4 = 3 + 1 + 1 = 5 и р3 = (0 + 1 + 1 = 2). Аналогичным образом получены комплексные решения для второй декомпозиции, их получилось три (при сложении 2.1 и 2.4; 2.2 и 2.4; 2.3 и 2.4), и третьей – две (при сложении 3.1, 3.3 и 3.4; 3.2, 3.3 и 3.4).
Сравнивая комплексные решения каждой декомпозиции с общими решениями внутри нулевого семейства механизма (4), совпадающими являются только два, это решения: p5 = 4, p4 = 3, p3 = 3; p5 = 3, p4 = 5, p3 = 2. Дальнейшее исследование проведем по варианту, когда p5 = 4, p4 = 3, p3 = 3. Оно для первой декомпозиции является результатом сложения решений (1.1, 1.3 и 1.4), для второй – (2.1 и 2.4), для третьей – (3.1, 3.3 и 3.4) эти решения в таблице выделены подчеркиванием.
Составим систему уравнений, используя полученные результаты решений. Первое уравнение системы (5) соответствует второму общему решению (4) для всего механизма внутри нулевого семейства, второе – решению (1.1), третье – (1.3), четвертое – (1.4) первой декомпозиции. Пятое уравнение является решением (2.1), шестое – (2.4) второй декомпозиции, а седьмое – (3.1), восьмое – (3.3) и девятое (3.4) третьей декомпозиции. Отметим, что система (5) состоит из девяти уравнений, а число кинематических пар в рассматриваемом механизме десять.
Чтобы решить эту систему, необходимо обосновать еще одно уравнение. Как часто используется на практике, для более простой организации привода ведущее звено со стойкой О1 соединим кинематической парой пятого класса. Отметим, что принятое условие не противоречит полученной системе (5), так в её левой части, где присутствует это соединение, в правой – наличествует кинематическая пара пятого класса.
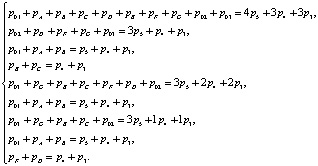(5)
Приступим к решению системы уравнений (5). Подставляя пятое уравнение системы в первое, получается, что рА + рВ = p4 + p3. Тогда в системе (5) окажутся два уравнения, тождественных полученному решению – это третье и шестое уравнения. Следовательно, в соединениях рА и рВ должны быть использованы пары p4 или p3. При подстановке девятого уравнения во второе находим, что р02 + рG + р03 = 3p5, т.е. в этих соединениях должны располагаться пары пятого класса. С учетом полученных решений система (5) имеет два тождественных уравнения: девятое и второе рF + рD = p4 + p3, а значит, рF = p4 или p3, а рD = p3 или p4. После идентификации кинематических пар в соединениях р01, р02, р03, рA, рВ, рG, рF и рD система будет содержать три тождественных уравнения (первое, пятое и седьмое), а именно, рЕ + рС = p4 + p3, где также должны находиться кинематические пары либо третьего (трехподвижные), либо четвертого классов (двухподвижные).
Итак, поставленная задача решена до конца, а именно, адресная замена шарниров в плоском восьмизвенном механизме на кинематические пары третьего и четвертого классов позволила создать принципиально новый безызбыточный по связям механизм дробилки (рис. 3, а). Проанализируем исследуемый механизм на соответствие условию Ассура, по которому любой механизм создается путем присоединения к ведущему звену (рис. 3, b), последовательно двух групп нулевой подвижности (рис. 3, c, d).
Ведущее звено (рис. 3, b) (n = 1, p5 = 1) имеет подвижность, определенную по формуле нулевого семейства W = 6n – 5p5 = 6·1 – 5·1 = 1, т.е. это механизм без избыточных связей.
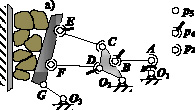
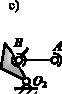
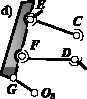
Рис. 3. Механизм без избыточных связей, условные изображения кинематических пар (а), ведущее звено (b), присоединяемые цепи (с, d)
Цепь АВО3 содержит два звена (n = 2), и по одной кинематической паре p5, p4 и p3, её подвижность W = 6n – 5p5 – 4p4 – 3p3 = 6·2 – 5·1 – 4·1 – 3·1 = 0, т.е. эта цепь есть пространственная группа нулевой подвижности – группа Ассура. Определим подвижность группы CEFDGО3. С учетом того, что в её составе четыре звена (n = 4) и кинематические пары p5 = 2, p4 = 2 и p3 = 2, W = 6n – 5p5 – 4p4 – 3p3 = 6·4 – 5·2 – 4·2 – 3·2 = 0, следовательно, и эта цепь является пространственной группой нулевой подвижности. И тогда, после присоединения этих групп к ведущему звену, весь механизм становится безызбыточным по связям, т.е. самоустанавливающимся, рациональным.
Заключение
Предложенный метод исключения избыточных связей в шарнирных механизмах является новым подходом к созданию структур механизмов с минимальным числом подвижных звеньев, не содержащих избыточных связей, в отличие от структур пространственных механизмов.
Кроме того, предлагаемая методика уже на этапе конструирования структурных схем позволяет решать вопрос об адресном расположении используемых кинематических пар для создания любых механизмов, в том числе и дробильных, без избыточных связей, а последующие кинематическое и силовое исследования позволят более точно определить требуемую мощность для технологического цикла и, как следствие, производить выбор электродвигателя без увеличения его мощности, по сравнению с существующими методиками расчета.