Любой проект проходит ряд этапов, которые неизбежно сталкиваются с задачей убедиться в правильности принятых решений и увидеть полученный результат еще до реального воплощения. В этом случае помогает модель. Сначала формулируются задача и цель моделирования. Затем анализируется объект моделирования, выбирается способ представления модели и средства реализации. Окончательно выполняется эксперимент и анализ результатов моделирования [1]. В такой последовательности рассмотрим создание модели привода с особым видом движения – скользящим режимом и переключаемой структурой.
Во время работы приводов при различных нагрузках и частотах вращения валов, возникают динамические процессы, зависящие от качества изготовления и монтажа электромеханических узлов, качества их сборки, степени изношенности механизмов, качества материалов, из которых выполнены узлы системы. Возникающие упругие поперечно-крутильные колебания валов и колес приводят к неравномерности перемещения рабочих механизмов, развитию зазоров в передачах и вместе с тем к ухудшению параметров движения исполнительных узлов системы. В конечном счёте это сказывается не только на качестве обработки поверхностей обрабатываемых изделий. Если при работе на относительно высоких скоростях источники возмущений могут оказывать пренебрежимо малое влияние на характер движения исполнительного механизма за счёт демпфирования, то при работе на низких скоростях проблема снижения качественных показателей движения становится существенной. Сложность качественного управления приводами на низких скоростях связана с ограниченным диапазоном регулирования по скорости и значительными силами сопротивления резанию и силами трения.
При выполнении технологических операций, включая и силовое взаимодействие, возрастает статическая нагрузка и изменяется инерционность, что влечет за собой изменение времени переходного процесса, нарушается устойчивость и динамическая ошибка. В обычных системах периодические возмущения могут привести к автоколебаниям.
Оптимизация конструкции предполагает устранение промежуточных механических передач, что в свою очередь требует компенсации упругих свойств передач при силовом взаимодействии.
Компенсация влияния изменения скорости частично решается с применением специальных методов управления в классе адаптивных систем. Этот класс глубоко разработан ведущими учеными России и за рубежом. Среди авторов работ можно назвать Е.П. Попова, И.М. Макарова, А.В. Тимофеева и других авторов. В теории управления и практическом применении методов адаптации для парирования возмущений авторами отмечается усложнение самих систем и трудности их настройки [2].
Разработанная в институте проблем управления по инициативе С.В. Емельянова [3] теория систем с переменной структурой показала новые возможности в теории систем управления. Уникальный режим движения в совокупности с изменяемой структурой позволяет значительно улучшить характеристики при возникающих внутренних возмущениях и снижение ошибок при внешних возмущениях.
В качестве примера рассмотрим электромеханический привод руки робота, который не охвачен обратной связью по выходной координате.
Целью исследования является создание модели привода с переменной структурой, исследование его работоспособности и возможности снижения неравномерности движения, вызванное возмущениями периодического характера, определяемого технологическим процессом.
Материалы и методы исследования
В качестве объекта будем рассматривать привод механизма перемещений с главной обратной связью по положению, причем сам механизм не охвачен обратной связью. Известные результаты исследований показали [4], что отсутствие полной информации о регулируемой координате резко снижает показатели работы привода, особенно при изменяющихся воздействиях, вызванных технологическим процессом.
Рассмотрим систему, которую можно описать каноническими уравнениями второго порядка [5]:
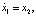
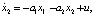(1)
где 
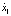и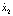 
переменные состояния и управляющее воздействие:
u = – Yx1. (2)
Здесь Y – параметр переключаемой структуры, величина которого может изменяться по закону
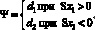(3)
Согласно теории систем с переменной структурой необходимо обеспечить условие, при котором произведение S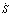
< 0. Для простоты реализации рассматривается система второго порядка. В качестве переменных используем ошибку регулятора положения и скорость вращения ротора двигателя. Если обозначить ошибку регулятора положения через x1, а скорость через x2, то уравнение скольжения запишется S = Сx1 + x2. Решение этого уравнения при с > 0 является устойчивым, и, следовательно, система с переменной структурой при произвольных начальных условиях также устойчива. Закон изменения структуры основан на анализе произведения Sx1. Для обеспечения стабилизации движения необходимо в управление добавить производную от координаты х1. Изменением структуры удастся парировать возмущение, недоступное для измерения. В этом случае можно добиться ошибки управления, близкой к нулю.
Представим разрабатываемую модель исходной схемой, реализующей рассматриваемый подход (рис. 1).
Перейдем теперь к выводу расчетных соотношений, которые позволят реализовать подход к построению системы с переменной структурой, предназначенной для управления движением объекта с неконтролируемыми возмущениями.
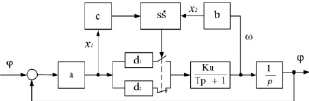
Рис. 1. Электромеханическая система
Будем рассматривать систему, представленную на рис. 1, с исполнительным устройством, описываемым уравнением
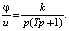
Представим предыдущее выражение уравнениями в пространстве состояний, аналогичное (1):
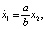
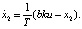
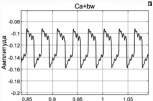
В этом выражении x1 = aφ, x2 = bw и a и b – коэффициенты, связывающие параметры датчиков с характеристиками привода.
Линия переключения определяется в соответствии с уравнением S = сx1 + x2 (с – положительная константа), а производная
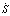= (cа/b – 1/T) x2 + (bkY/T) x1.
Вблизи линии переключения x2 = –cx1, поэтому
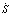= (–cа/b + 1/T ) c x1 + (bkY/T) x1.
В силу необходимости выполнения условия S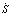
< 0, имеем
[–c2а/b + c/T + bkY/T] x1S < 0.
Переключение структур основано на анализе произведения x1S
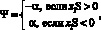
и с учетом (2, 3) управление изменяет свой знак.
Величина a вычисляется по выражению
a = T/bk(c2а/b + c/T).
Результаты исследования и их обсуждение
Теперь можно построить модель привода. В качестве инструментальных средств будем использовать программную систему Matlab. Встроенный в Matlab пакет структурного моделирования Simulink дает возможность простыми и выразительными средствами построить компьютерную модель и выполнить визуализацию результатов [5, 6]. Модель, построенная с использованием стандартных блоков Simulink, приведена на рис. 2. Схема включает следующие блоки. Схема вычисления произведения S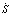
содержит блок суммирования (сумматор 1), блок произведения и инвертор. Переменная а перемножается с константой с, проходя через усилитель С, и поступает на вход сумматора, на второй вход которого подается сигнал, представляющий собой произведение коэффициента b на угловую скорость (усилитель b), снимаемую с выхода исполнительного устройства. В результате вычисляется параметр линии переключения 
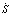. Блок произведения обеспечивает перемножения 
на параметр перемещения a. В результате получаем условие переключения S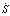
. Выход инвертора управляет переключением структур с помощью ключа.
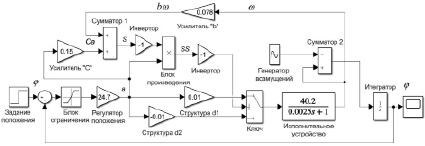
Рис. 2. Модель привода
Исследование возмущающих режимов проводилось с использованием генератора задающего периодические сигналы различной амплитуды и частоты, построенного с использованием стандартного блока синусоидальных сигналов и сумматора 2.
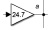
Для эксперимента установим параметры модели К = 40,2, Т = 0,0025, а = 24,7, b = 0,078.
В этом случае параметр a = 0,00079 (316,6с2 – 400с) = -0,0417. Величина с определяет наклон линии скольжения, значение которой должно быть менее 0,2, а значение коэффициентов переключаемых структур |d| < 0,04.
Приведенные расчетные соотношения адекватно отражают поведение работы системы с переменной структурой и скользящим режимом движения.
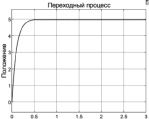
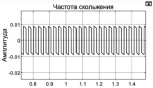
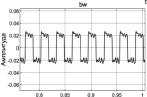
Проверим влияние изменения параметров привода на выходные характеристики. Изменим параметры регулятора положения в интервале от 10 до 25 и характеристики исполнительного устройства К от 20 до 40 и Т от 0,025 с до 0,0003 с. Диапазон изменения параметров выбран со значительным разбросом, что не характерно для реальных систем, но отражает возможности рассматриваемой модели. Снижение коэффициента исполнительного устройства в 2 раза не приводит к существенным изменениям, а снижение коэффициента регулятора положения снижает частоту переключения с 30 Гц до 16 Гц. Остальные параметры не претерпевают изменений. Изменение коэффициента b на порядок увеличивает частоту переключений до 200 Гц и повышает точность. Напротив снижение параметра с до 0,1 приводит к снижению частоты скольжения при незначительном снижение остальных параметров. Изменение постоянной времени исполнительного устройства при снижении постоянной времени до 0,0025 с снижает частоту переключений до 20 Гц, а при 0,025 с до 8 Гц и уровень отклонения от установившегося значения незначительно увеличивается.
Кроме того, чтобы убедиться в инвариантности к параметрическим изменениям и структурным преобразованиям заменили исходное исполнительное устройство моделью силового преобразователя (апериодическое звено 0,002р + 1 = 7u) и двигателя (колебательное звено 10-4p2 + 0,005p + 1 = 0,8u). Переходный процесс полностью совпадает с исходной схемой.
Единственным дополнением в схеме было согласование коэффициента обратной связи по скорости. Таким образом, правильно сформированное пространство скольжения действительно обеспечивает инвариантность.
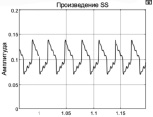
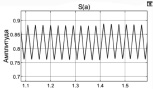
Результаты, полученные в процессе моделирования, представлены в таблице. В таблице приведено пространство состояния в виде выходных сигналов, точки съема информации и контролируемый параметр. Приведенные результаты соответствуют режиму работы без внешних возмущений.
|
Пространство переменных состояния |
||
|
Контролируемый параметр |
Точка контроля |
Вид выходного сигнала |
|
Переходный процесс по угловому положению |
|
|
|
Входное воздействие на исполнительное устройство. Сигнал скольжения (частота переключения) |
|
|
|
Произведение сигнала линии переключения на ее производную |
|
|
|
Сумма сигналов положения и скорости с учетом коэффициентов согласования |
|
|
|
Сигнал перемещения |
|
|
|
Скоростной сигнал |
|
|
Рассмотрим теперь влияние внешнего возмущения на характер движения выходной координаты. Будем задавать возмущение в интервале 0,1 В до 2 В и частоты от 10 рад/с до 31 6рад/с. При амплитуде от 0,01 В и частоте от 10 до 150 рад/с возмущений частота скользящего режима больше 200 Гц и отклонение от установившегося значения не более 0,01 %.
С ростом амплитуды возмущений до 2 В при тех же условиях приводит к незначительному снижению частоты скольжения и отклонению относительно установившегося режима 0,4 %. Наихудший вариант получен при частоте возмущений 10 рад/с и амплитуде 2 В. Значительно снижается частота скольжения (1,42 Гц) при относительно малом увеличении отклонении от установившегося значения (5,6 %). В реальных условиях возмущение не может быть больше возможности исполнительно устройства.
Заключение
Рассмотренная модель привода, реализующая рассмотренный принцип управления, способна обеспечить заложенные в нее возможности параметрической компенсации различных видов возмущений. Разрабатываемый привод принципиально реализуем.
Приведенные исследования убедительно доказывают инвариантность к изменению внутренних параметров и внешних возмущений.
К недостаткам рассматриваемой модели привода относится небольшая частота переключений, связанная с постоянной времени исполнительного устройства. В силу этого в выходном сигнале появляются периодические отклонения от установившегося значения 0,1 % при оптимальном режиме работы и 1 % при максимальной амплитуде и низкой частоте возмущений.