Рассмотрим систему обыкновенных дифференциальных уравнений (ОДУ)
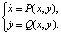(1)
Здесь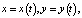 
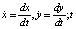будем называть временем, P, Q – заданные нелинейные функции переменных x, y. Известно, что каждому решению 
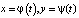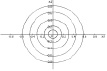
системы (1) на плоскости (x, y), называемой фазовой, отвечает некоторая кривая, иначе траектория или орбита. Если кривая замкнута, то ей отвечает периодическое (т.е. колебательное) движение, если кривая вырождается в изолированную точку, то говорят о состоянии равновесия. Состояния равновесия определяются из системы (1), если в ней положить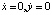 
. В простейших случаях состояния равновесия делятся на узловые, седловые, фокусы и центры (рис. 1). Тип состояния равновесия определяется в результате линеаризации системы в его окрестности и решения соответствующего характеристического уравнения [1, 2]. Если траектория при t → +∞ или при t → –∞ стремится к седловому состоянию равновесия, то она называется сепаратрисой седла. Если сепаратриса при t → +∞ стремится к одному седловому состоянию равновесия, а при t → –∞ – к другому седловому состоянию равновесия, то она называется гетероклинической траекторией, а соответствующее ей решение перепадом. Если сепаратриса как при t → +∞, так и при t → –∞ стремится к одному и тому же седловому состоянию равновесия, то она называется петлей сепаратрисы или гомоклинической траекторией, а соответствующее ей решение называется солитоном. Гомоклиническая траектория не соответствует периодическому решению, движение по ней происходит за бесконечное время. Термин «сепаратриса» происходит от французского «separer», что в переводе означает разделять. Сепаратриса делит фазовую плоскость на части, поведение траекторий в которых качественно различно. Например, в теории волн [3, 4] известна система 
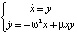и её первый интеграл 
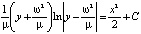. Одна из траекторий системы – прямая, разделяющая фазовую плоскость на части: в одной – все траектории замкнуты (отвечают колебаниям), в другой – не замкнуты (колебания отсутствуют) (рис. 2).
a) b) c) d)
Рис. 1. Узел (a), седло (b), фокус (c), центр (d)
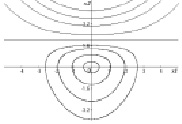
Рис. 2. Сепаратриса делит плоскость на части с разным качественным поведением траекторий
Целью статьи является изложение краткой методики обучения нахождению частных решений типа «солитон» и «перепада» в дифференциальных уравнениях 2-го порядка, встречающихся в теории колебаний. Эти понятия в курсах ОДУ втузов обычно не затрагиваются, хотя имеют большое теоретическое значение как для теории ОДУ, так и для её приложений в физике. Как показывает практика обучения математике в высшей школе, формирование исследовательских компетенций успешно происходит в случае учебно-исследовательской деятельности студентов [5]. Изложенные в статье соображения методического характера по обсуждаемому вопросу могут быть приняты во внимание преподавателями втузов как при проведении практических занятий, так и при организации учебно-исследовательской деятельности студентов в курсах математики [6–8].
Суть предлагаемой методики обучения заключается в следующем. На первом этапе проводится исследование сразу нескольких эталонных математических моделей на фазовой плоскости. Эти модели структурно близки и подобны. Здесь студенты, знакомясь с понятием первого интеграла, вырабатывают навыки построения семейства инвариантных кривых, отрабатывают алгоритм линеаризации системы в окрестности состояний равновесия, знакомятся с типами состояний равновесия и другими понятиями метода фазовой плоскости. При этом у учащихся формируются комплексные знания, так как они одновременно используются методы и приемы математического анализа, аналитической геометрии, алгебры. Результатом первого этапа решения задачи является визуализация первых интегралов на фазовой плоскости 
. Второй этап исследования непосредственно связан с поиском частных решений исходных уравнений солитонного типа, озаглавленных в названии статьи. При этом студенты вновь обращаются к тем же моделям, но уже с другим уровнем знаний и, опираясь на построенные фазовые портреты, ставят и решают задачи Коши. Особенность решения здесь заключается в правильном выборе начальных данных (тривиальные для преподавателей высшей математики шаги решения в статье опущены).
Фазовые портреты
Рассмотрим дифференциальное уравнение второго порядка
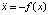. (2)
В механике оно называется уравнением Ньютона и описывает движения консервативной системы с одной степенью свободы. При этом x = x(t) – неизвестная функция (обобщенная координата),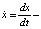 
производная (скорость), f(x) – заданная функция (квазиупругая сила), t – время. Наряду с уравнением (2) будем рассматривать и эквивалентную ему систему
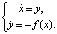(3)
Ясно, что система (3) есть частный случай (1), где P(x, y) = y, Q(x, y) = –f(x), причем все состояния равновесия её находятся на оси x и являются центрами либо седлами. Последнее следует из типа корней характеристического уравнения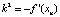 
, где xn – абсцисса положения равновесия с номером n: f(xn) = 0.
Хорошо известно, что система (3) интегрируется [2]. Ее первый интеграл U(x, y), отвечающий за закон сохранения полной механической энергии, легко находится. Действительно, из (3) находим уравнение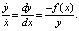 
После разделения переменных и интегрирования получаем
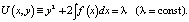(4)
Уравнение (4) представляет собой однопараметрическое семейство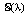 
дифференциальных уравнений первого порядка, так как 
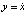. При этом равенству (4) на плоскости (x, y) для каждого λ (это первая произвольная постоянная интегрирования) отвечает инвариантное множество, состоящее из траекторий. Совокупность всех инвариантных множеств представляет собой фазовый портрет и характеризует поведение системы в целом. Видно, что каждое уравнение из семейства (4) эквивалентно двум: 
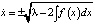(знак «+» отвечает движению точки в верхней полуплоскости (y > 0) слева направо, знак «–» – за движение в нижней полуплоскости (y < 0) справа налево). Разделяя переменные в последнем уравнении, получим 
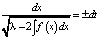. Отсюда находится общий интеграл (общее решение в неявном виде)
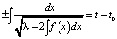
(t0 – вторая произвольная постоянная). (5)
При этом говорят, что уравнение (2) проинтегрировано в квадратурах. Как видно, получение формулы (5) никаких сложностей не представляет.
Замечание. В курсах обыкновенных дифференциальных уравнений после нахождения общего интеграла (5) часто делается заключение, что задача решена. Однако задачей теории дифференциальных уравнений является не только нахождение решения или решений, но и изучение их свойств. Изучение же функций x = x(t), заданных неявно, как в нашем случае, представляет, как правило, не простую задачу, которую часто опускают. Трудности возникают уже в простейших случаях правых частей вида
, 
,
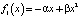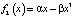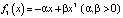и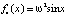 
,
которые в приложениях играют важную роль. Связаны они с проблемой обращения так называемых эллиптических интегралов [4, 9]. Конечно, эти вопросы подробно изучаются в специальных курсах теории колебаний для физиков и с ними можно познакомиться по книгам [4, 10]. Здесь же мы ограничимся обсуждением некоторых простых, но важных частных решений дифференциального уравнения (2), определяемых равенством (5) для случаев fk(x), k = 1, 2, 3, 4, с которыми необходимо познакомить студентов уже в курсе дифференциальных уравнений общеинженерного профиля.
Для начала рассмотрим фазовые картины этих уравнений. При этом, не умаляя общности рассуждений, будем считать α = 1, β = 1.
Пример 1. Пусть в уравнении (2) f(x) = –x + x2. Тогда в системе (3) будет два положения равновесия: C0 (0,0) – седло и C1 (1,0) – центр, а интеграл (5) примет вид
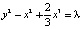. (6)
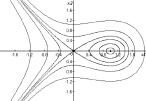
На рис. 3 мы привели инвариантные множества, отвечающие разным значениям параметра λ. В частности, равенству λ = 0 будет отвечать множество, состоящее из четырёх траекторий: двух незамкнутых сепаратрис седла, положения равновесия C0 и петли сепаратрисы (гомоклинической траектории). На рис. 4, а, приведено семейство «всех» инвариантных кривых, образующих фазовый портрет системы в этом случае. Видно, что существует область, охватываемая петлёй сепаратрисы, все траектории в которой замкнуты, т.е. периодические, а следовательно, отвечают колебательным процессам.
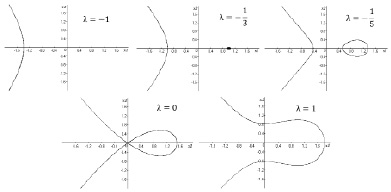
Рис. 3. Инвариантные множества
a) b)
c) d)
Рис. 4. Фазовые портреты эталонных систем
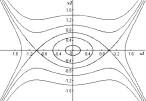
Пример 2. Пусть в уравнении (2) f(x) = x – x3. Тогда в системе (3) будет три положения равновесия: центр C0(0,0) и два седла C1,2(±1,0), а интеграл энергии (5) примет вид
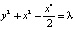. (7)
Множество инвариантных кривых, отвечающих интегралу (7), представлено на рис. 4, b. Область колебательных движений в этом случае ограничивается двумя седлами и двумя сепаратрисами, идущими из одного седла в другое. Такие траектории называются гетероклиническими (движениями двояко асимптотическими при t → ±∞ к седлам).
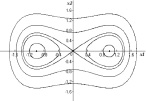
Пример 3. Пусть в уравнении (2) f(x) = –x + x3. Тогда в системе (3) будет также три положения равновесия, только C0(0,0) будет седлом, а C1,2(±1,0) – центрами, а интеграл энергии примет вид
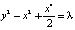. (8)
Множество инвариантных кривых, отвечающих интегралу (8), представлено на рис. 4, с. Область колебательных движений, возникающих около состояний равновесия C1,2(±1,0), в этом случае ограничивается двумя сепаратрисами седла. Они образуют, как говорят, гомоклиническую восьмёрку, которая возникает при λ = 0.
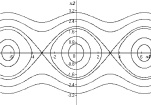
Пример 4 (математический маятник). В этом случае f(x) = ω2sinx, и в системе (3) счетное множество состояний равновесия: центры C(2πn, 0) и седла C(π + 2πn, 0), а интеграл энергии имеет вид
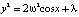. (9)
Заметим, что центрам отвечают нижние состояния равновесия маятника, т.е. устойчивые, седлам – верхние, т.е. неустойчивые состояния равновесия. Фазовый портрет системы представлен на рис. 4, d. Область колебательных движений, как и в случае примера 3, ограничивается сепаратрисными (гетероклиническими) контурами, идущими из седла в седло. При этом фазовый портрет является периодическим с периодом 2π.
Солитонные решения и движения по сепаратрисам
Выведем теперь решения уравнений (6)–(9), которым отвечают движения по гомоклиническим и гетероклиническим траекториям.
Пример 1 (продолжение). Выше мы уже отмечали, что в интеграле (6) значению λ = 0 отвечает инвариантное множество, включающее петлю сепаратрисы, которая, как несложно понять, находится в полосе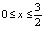 
(рис. 4, a). Искомое движение легко найдется в результате решения задачи Коши для дифференциального уравнения
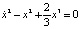, (10)
если за начальное условие взять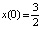 
. Действительно, уравнение (10) в полосе 
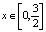эквивалентно двум уравнениям, с разделяющимися переменными
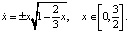(11±)
Причем функция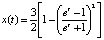 
будет решением уравнения (11–) при t∈[0, +∞) и решением (11+) при t∈(–∞, 0). Таким образом, функция 
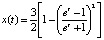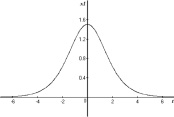
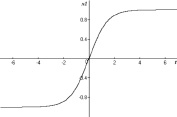
будет решением уравнения (10) на всей вещественной оси. Последнюю функцию можно представить через гиперболический тангенс так: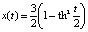 
. Интегральная кривая этого решения изображена на рис. 5, a. Видно, что при t → ±∞ решение x(t) → 0. В физике такие решения называют решениями типа «солитон».
a) b)
Рис. 5. Графики решений типа «солитон» (a) и «перепада» (b)
Пример 2 (продолжение). Рассмотрим теперь первый интеграл системы (7) при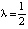 
. Нетрудно проверить, что соответствующее инвариантное множество включает четыре сепаратрисы и два седла C1,2(±1,0) (рис. 4, b). Движение по гетероклинической траектории, расположенной в области y > 0 найдется в результате решения задачи Коши для уравнения 
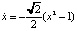с начальным условием x(0) = 0:
, 
.
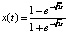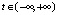Последнее решение представляет собой гиперболический тангенс
, 
.
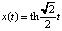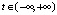На рис. 5, b, изображена интегральная кривая этого решения. Видно, что при t → ±∞ решение x(t) обладает асимптотическим свойством x(t) → ±1. В физике такое решение называют уединенной волной типа «перепада».
Пример 3 (продолжение). Рассмотрим теперь первый интеграл системы (8) при λ = 0. Движение по гомоклинической траектории, расположенной в области x > 0, найдется в результате решения задачи Коши для уравнения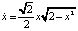 
с начальным условием 
:
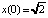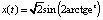, t∈(–∞, +∞).
Последнее решение можно представить через гиперболический косинус:
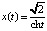, t∈(–∞, +∞).
Из свойств функции сht следует, что при t → ±∞ решение x(t) → 0.
Решение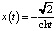 
, t∈(–∞, +∞) соответствует движению по левой петле сепаратрисы.
Пример 4 (продолжение). Наконец рассмотрим первый интеграл системы уравнений маятника (9) при λ = 2ω2. При этом значении λ соответствующее инвариантное множество содержит седла и гетероклинические траектории (рис. 4, с). Уравнение этого множества имеет вид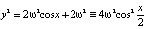 
. Отсюда вытекают два дифференциальных уравнения первого порядка
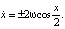(12±)
Уравнение (12+) описывает движения маятника по сепаратрисе в верхней полуплоскости, уравнение (12–) – в нижней. Интегрируя уравнение (12+), находим решение
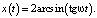(13)
Видно, что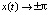 
(t → ±∞), т.е. (13) является решением типа перепада.
Заметим, что решения типа «солитон» и «перепад» не являются периодическими. Они определены на всей вещественной оси, образуют границу периодических (колебательных) движений и физически не реализуются. Из сказанного также вытекает, что колебательные режимы будут возникать: 1) в случае характеристики f(x) = –x + x2 при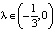 
; 2) в случае характеристики f(x) = x – x3 при 
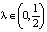; 3) в случае f(x) = –x + x3 при 
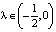; в случае 
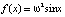при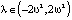 
. Эти движения будут описываться эллиптическими функциями, которые занимают промежуточное положение между тригонометрическими и гиперболическими функциями.
Заключение
Предлагаемая схема обучения решению поставленной задачи имеет определенную новизну и неоднократно апробировалась на практике, при этом отмечался устойчивый интерес студенческой аудитории, как к постановочной части, так и алгоритму ее решения. Определенный прогресс в обучении, как нам кажется, здесь достигается за счет опоры схемы (алгоритма) решения на геометрические образы – фазовые портреты. Подчеркнем, что рассмотренные примеры, с одной стороны, являются простыми, с другой – эталонными, т.е. практически значимыми.
Как мотивировать студента к научно-исследовательской деятельности, как развивать его творческие способности, как вырабатывать исследовательские навыки, как побуждать учащегося к познавательной деятельности в конкретной научной области, какие технологии обучения исследовательской деятельности применять и в каком направлении их развивать? Подобных вопросов много и ответы на них, как правило, трудны и неоднозначны. Однако на некоторые вопросы ответы есть и связаны с анализом содержания учебных дисциплин и в первую очередь с набором задач, рассматриваемых в них. Роль задач и примеров в образовании вообще и в высшей технической школе в частности чрезвычайно велика. Именно через самостоятельную деятельность в процессе решения задач, физическая постановка которых интересна и понятна студенту (мы это подчеркиваем), он проникается интересом к предмету обучения. Поэтому подбор задач чрезвычайно важен и не должен быть случайным. В высшей степени сказанное относится к разделу ОДУ. Как отмечал академик Л.С. Понтрягин, наиболее важные и интересные технические применения ОДУ находят в теории колебаний и теории автоматического управления. Следуя этому завету, мы остановились на методическом обсуждении нескольких примеров из теории колебаний и ограничились одной важной задачей – поиском частных решений типа «солитон» и «перепад». Задача нестандартная для курса ОДУ по постановке и требующая неформального комплексного подхода (знаний из разных разделов математики). Разыскиваемые частные решения связаны с интересным физическим явлением, называемым волнами цунами, поэтому прикладная сторона здесь вполне конкретна. Другие решения рассмотренных в статье уравнений, как мы отметили, связаны с эллиптическими функциями. Их поиск может составлять второе направление учебно-исследовательских задач и являться предметом другой статьи.