Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

Любые научные исследования, касающиеся использования и обработки полученных данных, в различных областях, как в социологии, экономике, физике, так и в педагогике, не могут обойтись без использования математического аппарата [1–3].

Современному специалисту любого профиля важно уметь обрабатывать и верно интерпретировать полученную информацию.

Современные исследования демонстрируют все большую необходимость применения математически обоснованных методик для получения достоверных результатов при применении педагогических экспериментов [4–6].

В педагогических исследованиях эксперимент является одним из важных способов проверки правильности гипотезы, иногда это единственно возможный способ проверки [7].

Как считают некоторые авторы, теория проверки гипотез применяется не всегда корректно, ей не уделяется должного внимания для проверки и верификации предположений [8–10].

Многие исследователи используют методы проверки гипотез для подтверждения предположений, выдвинутых на начальных этапах эксперимента. Однако иногда анализ полученных результатов и используемых в работах методик показывает, что авторы неверно интерпретируют результаты и порой некорректно обрабатывают их. Данную информацию подтверждают некоторые независимые исследования, проводимые на основе диссертационных работ по психолого-педагогическим специальностям [11].

Именно использование методов математической статистики позволяет выявить закономерности по полученным в результате эксперимента данным.

Одним из разделов математической статистики является теория проверки гипотез, которая позволяет проводить проверку предположений и получать обоснованные результаты исследования, основываясь на критериях проверки гипотез, в которых используются стандартные алгоритмы. Отметим, что, несмотря на универсальный характер статистических методов, многие из них имеют ряд ограничений, что необходимо учитывать при выборе критерия проверки и его реализации.

Гипотезой можно назвать любое предположение о свойствах генеральной совокупности. Но любая гипотеза должна быть обоснована и должна отражать вопрос исследовательской задачи.

Когда речь идет о выборочных данных, следует учитывать, что под ними понимается лишь часть статистических данных генеральной совокупности. В связи с этим необходимо проводить отбор данных для выборки таким образом, чтобы выборка отражала свойства генеральной совокупности наиболее полно, то есть была репрезентативной.

Цель данной работы: показать основную методологию исследования влияния применения новой технологии в обучении на основе полученных статистических данных.

В педагогических исследованиях часто возникают исследовательские задачи, связанные с применением новой методики преподавания, новой технологии и т.д. [12–14]. Методы проверки гипотез могут быть использованы в данном случае для подтверждения эффективности новой методики, новой технологии и т.д.

Если в экспериментальной части работы мы проведем лишь сравнение средних значений (например, сравнение среднего балла результатов контрольной работы, написанной в двух классах, занимающихся по разным методикам) и сделаем вывод о положительном влиянии новой методики, то этот результат не будет обоснованным, так наблюдаемые различия выборочных средних (средний балл) могут лежать внутри границ случайных колебаний.

Больше информации можно получить, если использовать визуальный анализ данных и провести построение полигона частот или гистограмм, а обоснованные выводы могут быть сделаны лишь после проверки статистической гипотезы.

Рассматриваемая далее методология позволит исследователю-педагогу сориентироваться в использовании основных алгоритмов проверки гипотез при проведении педагогических экспериментов.

Последнее время педагоги различных дисциплин более активно стараются использовать новые методы преподавания, внедряют в дисциплины элементы новых технологий, ожидая успеха от реализации этих методов.

Часто эти методы показывают оптимистичный результат и, получив повышение среднего балла в классе или группе, где проводилось внедрение новой образовательной технологии, исследователь делает выводы, что полученные результаты показывают положительное влияние проведенного эксперимента. Однако к исследователю могут возникнуть вопросы: не связано ли повышение среднего балла с изучением более легкой темы раздела преподаваемой дисциплины, чем ранее изучаемая? Не связано ли повышение среднего балла в связи с переносом времени занятий на более удачное, когда ученики приходят на занятие неутомленные, в отличие, например, от последней пары/последнего урока, когда сосредоточенность на изучаемом предмете уже теряется? Возможно, повышение среднего балла произошло в связи с тем, что изменился состав учеников и т.д. Таким образом, исследователю нужно доказать, что успешные полученные результаты были получены именно благодаря применению новой технологии, а не за счет случайных неучтенных факторов.

В этом контексте становится очевидным преимущество применяемых для проверки гипотез методов, которые позволяют обосновать утверждение, подтвердив, что на результат не повлияли неучтенные при проведении эксперимента факторы.

Материалы и методы исследования

Объясним подробнее, основываясь на классической формулировке исследовательской задачи, алгоритм проверки эффективности применения новой технологии.

Педагог реализует новую методику преподавания какой-либо дисциплины. Выдвигается предположение, что новая методика эффективнее стандартных ранее применяемых методов.

Так как полученные зафиксированные результаты предполагают сравнение, следует провести один из видов тестирования, например, проверочную тестовую работу, позволяющую зафиксировать результаты в обеих группах.

Далее происходит сравнение результатов обучения в этих группах.

Если результаты второй группы, занимающейся с использованием новой технологии, оказались лучше результатов первой группы, то рано делать выводы об эффективности применяемой методики. Следует проверить гипотезу, используя теорию проверки статистических гипотез, чтобы выяснить, действительно ли новая методика дает лучшие результаты или различие результатов возникло случайно, за счет случайных факторов, и тогда новую методику нельзя считать лучше стандартной ранее применяемой.

Основная ошибка, которую делают неопытные исследователи, пытаясь сделать выводы о лучших результатах в группе, заключается лишь в сравнении средних значений в этой группе. Как, например, при проведении занятий по новой технологии в одном классе и проведении занятий по старой технологии в другом классе, мы получили результат: средний балл по итоговому тестированию в группе с новой технологией составил 4,3, в то время как в другом классе этот результат 3,9. Сразу же делать вывод об эффективности будет ошибкой. Этот результат не обоснован. Могут возникнуть следующие вопросы: однородны ли были исследуемые группы (одинаковый ли уровень подготовки у учащихся обоих классов), не повлияли ли на этот результат случайные неучтенные в исследовании факторы и т.д.

Именно в этом случае для научного обоснования эффективности выдвигается гипотеза и используется математический аппарат проверки.

Следует заметить, что методы математической статистики никогда не позволяют доказать гипотезу, а только подтвердить или опровергнуть, насколько хорошо предположение согласуется с полученными данными.

Чтобы реализовать проверку данной гипотезы, необходимо рассмотреть две группы: экспериментальную и контрольную. Учащиеся первой группы занимаются по стандартной ранее применяемой технологии, учащиеся второй группы – занимаются с использованием новой технологии преподавания.

Опишем, как проводится реализация проверки гипотез. На первом этапе выдвигается основная (или нулевая гипотеза) и формулируется альтернативная ей.

Проверку основной гипотезы можно проводить с помощью различных статистических критериев [8–10].

В случае если в результате проверки основная гипотеза не отвергается, то это означает ее принятие и свидетельствует о совместимости с выборочными данными.

Часто в качестве основной гипотезы формулируется утверждение, доказательство которого нежелательно для проводящего исследование, а опровержение гипотезы позволяет подтвердить полученные результаты, например эффективность применения новой технологии.

Заметим, что при проверке гипотез необходимо, чтобы закон распределения критерия был известен.

При проверке гипотезы выбирается так называемый критерий проверки. Какой именно из критериев выбирается, зависит от формулировки основной и альтернативной гипотез, а также от того, какие выборочные или теоретические данные известны. По фиксированной формуле в соответствии с используемым критерием по выборочным данным находятся наблюдаемое и выборочное значения критерия, иначе статистика критерия.

При проведении вычислений выбирается уровень значимости, который означает вероятность ошибки, заключающейся в отклонении основной (нулевой) гипотезы, в то время как она является верной. Часто для расчетов выбираются значения 0,05 или 0,01, что соответствует вероятности ошибки 5 % или 1 %.

Множество значений критерия состоит из двух непересекающихся подмножеств, которые называют допустимой областью и критической областью. При попадании в допустимую область принимается основная гипотеза, при попадании в критическую область – альтернативная.

Точки, разделяющие множество значений критерия на допустимую и критическую области, называются критическими точками, их значения можно найти, используя таблицу распределения для выбранного критерия. Среди наиболее часто используемых распределений при проверке гипотез можно отметить распределение Стьюдента, распределение Фишера, распределение хи-квадрат и др.

Таким образом, общий алгоритм проверки гипотезы заключается в следующих этапах. Сначала выбирается критерий проверки, затем вычисляются два значения – одно из которых считается по формуле, представленной для каждого конкретного критерия с использованием статистических данных конкретной выборки, другое значение может быть получено по таблице распределений, исходя из критерия проверки (ранее мы перечисляли основные распределения, которые используются при проверке гипотез – хи-квадрат, Фишера, Стьюдента и др.) Два полученных числовых значения сравниваются и делается вывод о попадании результата либо в допустимую область, либо в критическую область. В первом случае принимается основная гипотеза, во втором случае принимается альтернативная гипотеза.

Следует отметить, что большую часть методов математической статистики, предназначенных для обработки статистической информации, не следует рассматривать как универсальный инструмент, готовый к использованию для любых выборочных данных. Так, например, критерий Стьюдента, дисперсионный анализ требуют нормальности распределения эмпирических данных, то есть соответствия нормальному закону распределения, также они могут быть применены лишь для шкал отношений и интервальных шкал. Соответствующие ограничения необходимо учитывать при выборе методов обработки данных и интерпретации результатов.

Если исследователя интересует сравнение двух независимых выборок (например, анализ результатов обучения в двух разных классах/группах), в которых данные подчинены нормальному распределению, то для непарных, независимых (несвязанных) выборок следует применить t-критерий Стьюдента. Заметим, что для сравнения трех и более групп данный критерий не подходит. Парный критерий Стьюдента следует применять, если сравниваются только две группы, то время как дисперсионный анализ повторных наблюдений можно использовать при наличии трех и более групп [15].

Если исследователь рассматривает случай «зависимых выборок», то данная ситуация возникает, когда рассматривается один и тот же набор объектов (группа) до и после оказания влияния/воздействия на исследуемые объекты. В этом случае основное предположение состоит в том, что воздействие на объекты может повлиять на признаки, соответственно сместив их средние значения в большую или меньшую сторону. Тогда необходимо провести проверку гипотез для двух выборок в случае зависимых выборок (обычно рассматриваются парные наблюдения).

Например, в группе на занятиях физической культурой проводится комплекс новых тренировок. До проведения тренировок для каждого из участников группы фиксируются баллы, отражающие физическую подготовку. Далее для каждого из участников фиксируются баллы после цикла проведения тренировок. В контексте данной формулировки рассматривается задача проверки гипотез для двух выборок, случай зависимых выборок, парных наблюдений.

Заметим, что если распределение изучаемого количественного признака в генеральной совокупности отличается от нормального, то тогда необходимо применять непараметрические критерии, которые не предполагают подчинения данных какому-либо закону распределения, в том числе и нормальному [15, 16].

Если необходимо сравнить две независимые совокупности, данные в которых не подчиняются закону нормального распределения, можно воспользоваться критерием Манна – Уитни, который иногда называется критерием Вилкоксона для непарных выборок [15].

Одним из самых популярных статистических критериев является критерий Стьюдента [9, 11, 12]. Его применение возможно при проведении педагогического эксперимента. Однако необходимо выполнение определённых требований для получения точных, объективных результатов.

Критерий Стьюдента для непарных выборок предназначен для сравнения средних величин количественных признаков в двух независимых группах. Его возможно применять, если признак в каждой из групп подчиняется закону нормального распределения и дисперсии в обеих группах равны, некоторые авторы предлагают вводить дополнительные ограничения на использование критерия Стьюдента [16].

Проверка распределения может проводиться с использованием графических методов или статистических критериев. При небольшом объёме выборки проверку гипотезы о виде функции распределения проводят приближёнными методами – графическим методом или по асимметрии и эксцессу [17, 18]. Проверка условия равенства генеральных дисперсий осуществляется с помощью выборочных данных.

В случаях, когда необходимые условия для применения критерия Стьюдента не соблюдаются, результаты исследования могут быть ошибочны [19].

Статистический критерий хи-квадрат также предназначен для сравнения двух статистических выборок. Метод проверки по критерию хи-квадрат может быть использован как для проверки однородности двух групп до начала проводимого эксперимента (чтобы показать, что при разбиении групп на контрольную и экспериментальную группы были проверены на однородность), так и для того, чтобы проверить, что после проведения эксперимента группы показали неоднородность (т.е. применяемая технология повлияла на результаты обучения).

Критерий χ2 (хи-квадрат) имеет ограничения, как и другие статистические критерии проверки гипотез [3].

Рассмотрим основные этапы, которые должны быть реализованы при проверке гипотезы об эффективности применения новой технологии на основе проведения эксперимента с математическим обоснованием, предполагающим использование элементов математической статистики.

Для представления выборки используется дискретный ряд (табл. 1), где все значения признака в таблице представлены в порядке возрастания, либо интервальный ряд (табл. 2, где i – число интервалов, на которые разбивается ряд).

Таблица 1

Общий вид дискретного ряда

Таблица 2

Общий вид интервального ряда

Основными числовыми характеристиками, применяемыми при изучении выборки и получении первичных результатов, являются выборочное среднее и выборочная дисперсия:

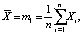(1)

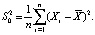(2)

Так как последняя оценка оказывается смещенной, рассматривают так называемую исправленную выборочную дисперсию:

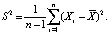(3)

Для проверки эффективности новой технологии можно проверить гипотезу о равенстве средних значений (из каждой группы) при известных дисперсиях (или же в случае неизвестных дисперсий).

Тогда нулевую (основную) гипотезу можно сформулировать как H0: ax = ay, а альтернативную гипотезу H1: ax > ay, где ax, ay – средние значения (средний балл) в каждой из групп. Альтернативную гипотезу целесообразно сформулировать в этом виде, так как её справедливость будет означать эффективность применения новой технологии.

Для проверки вычисляется статистика критерия 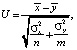где n, m – количество элементов первой и второй выборки соответственно, 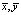– выборочные средние первой и второй выборок, 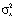, 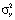– известные дисперсии для первой и второй группы.

Критическая точка выбирается из условия Φ0(uкр) = 1/2 – α. Если U < uкр, то нулевая гипотеза принимается, если U > uкр – отвергается (то есть верно предположение об эффективности технологии). Значения критической точки находятся из таблицы функции Лапласа.

Таким образом обычно проверяется и гипотеза о средних и в случае неизвестных дисперсий для больших выборок (порядка сотен), когда оценки дисперсий можно принять за их точные значения.

В случае неизвестных равных дисперсий гипотеза о равенстве средних проверяется следующим образом.

Нулевая гипотеза формулируется как H0: ax = ay, а альтернативная как H1: ax > ay. В случае подтверждения альтернативной гипотезы H1 делаем вывод об эффективности применяемой технологии. Альтернативную гипотезу целесообразно сформулировать в этом виде, так как её справедливость будет означать эффективность применения новой технологии.

Для проверки вычисляется статистика критерия 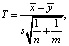где 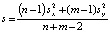– объединённая оценка дисперсии (общей для выборок).

Для проверки берутся критические точки tкр распределения Стьюдента с n + m – 2 степенью свободы и уровнем значимости α (степень свободы и уровень α являются параметрами данного распределения), если T < tкр, то нулевая гипотеза принимается, если T > tкр – отвергается. При применении этого метода предполагается равенство дисперсий двух выборок, поэтому сначала необходимо проверить гипотезу о равенстве дисперсий [20]. Иначе этот метод применять нельзя.

Результаты исследования и их обсуждение

Приведем один из алгоритмов проверки гипотезы, учитывая специфику исследовательской задачи.

Предполагается, что добавление элементов геймификации в дисциплины политехнического цикла оказывает положительное влияние на успеваемость обучающихся.

Для исследования предлагается рассмотреть две группы: контрольную и экспери- ментальную.

В экспериментальной группе учащихся в ходе эксперимента будем проводить занятия с использованием элементов геймификации, в контрольной группе учащихся будем проводить занятия в обычном режиме.

Важно, чтобы две группы, результаты по которым будут сравниваться, первоначально практически не различались, что может гарантировать достоверность полученных результатов. Для этого можно проверить гипотезу об однородности. В этом случае выдвигается предположении, что все выборки произведены из одной генеральной совокупности или же совокупности, из которых взяты выборки, одинаковы.

Таким образом, следует отметить, что первоначально выбранные группы не должны различаться по возрасту (этого легко достичь, рассматривая классы одной параллели), до проведения эксперимента уровень знаний и методика преподавания в обоих классах не предполагают существенных различий.

Для того чтобы проверить однородность сформированных групп по уровню начальных знаний, можно воспользоваться критерием хи-квадрат Пирсона.

Например, рассматриваются два ряда наблюдений некоторого признака, и каждый ряд разбит на r групп (по значениям признака). Разбиение проведём по баллам учащихся, набранным в результате проведенного пробного тестирования r = 6. Максимальное число набранных баллов составляет 18. Приведены примеры таблицы для заполнения в контрольной группе (табл. 3) и в экспериментальной группе (табл. 4). В данных таблицах представлены значения проверочного тестирования до проведения педагогического эксперимента. Осуществим проверку однородности контрольной и экспериментальной групп. Общее число участников в контрольной группе составило 65 учащихся, в экспериментальной – 68 учащихся.

Результаты по баллам в обеих группах схожи, 44 учащихся в контрольной группе набрали 10 и более баллов, в экспериментальной группе число учащихся с баллом 10 и более составило 41 человек.

Сгруппированный ряд будет иметь вид

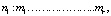
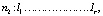
где mi, li – число выборочных значений в i-й группе соответственно для первого и второго наблюдений. Статистический критерий для проверки нулевой гипотезы имеет вид

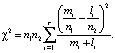(4)

При n → ∞, если основная гипотеза верна, критерий имеет предельное распределение хи-квадрат с r – 1 степенями свободы.

Проверка гипотезы проводится по алгоритму: если 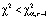, то нулевую гипотезу (предположение об однородности групп) будем считать верной, иначе – нет. Значение критической точки выбирается из таблицы распределения хи-квадрат для заданного уровня значимости и степени свободы.

Для данного примера n1 = 65, n2 = 68, r = 6: 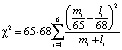= 0,004.

В соответствии с алгоритмом проверки гипотезы найдем критические значения по таблице распределения хи-квадрат 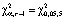= 11,1. По полученным данным 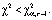Значение критической точки из таблицы распределения при уровне значимости 0,05 и 5 степенях свободы дает значение 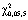= 11,1. Таким образом, 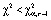, то есть основная гипотеза об однородности групп подтверждается.

В течение 2,5 месяцев в экспериментальной группе занятия проводились с использованием элементов геймификации, в контрольной группе занятия по программе того же объема проводились без применения новой технологии.

После проведения контрольного тестирования для групп были получены баллы, представленные в табл. 5, 6.

По результатам контрольного тестирования экспериментальная группа показала лучшие результаты, 53 учащихся набрали балл 10 и более, в то время как в контрольной группе количество таких участников составило лишь 39 учащихся.

Значение статистики по выборочным данным с применением формулы (4) составило χ2 = 205,62.

Таким образом, 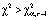, нулевая гипотеза отклоняется на уровне 0,05 и принимается альтернативная. На основе полученных значений можно утверждать, что новая технология, применяемая в экспериментальной группе, способствует лучшему усвоению материала и более высоким результатам.

Рассмотрим схему работы при использовании новой технологии в i-х классах.

1. Выбираем определённую параллель (например, i-е классы, по которым возможно собрать первоначальные данные), предполагая однородность выборки.

2. Выбираем один из предметов политехнического цикла (при ведении которого планируется добавить элементы геймификации или другую образовательную технологию).

3. Собираем данные о баллах учащихся i-х классах по этому предмету (например, проведение тестирования, проверочной работы и т.д.).

4. Проводим разбиение на две группы, первоначально проверив однородность данных (например, используя критерий однородности хи-квадрат).

5. После того как убеждаемся, что группы однородны, начинаем работу в экспериментальной группе (проводим занятия с использованием новой технологии).

6. По завершении экспериментального этапа собираем данные (проверочное тестирование) в экспериментальной и контрольной группах. Проводим проверку однородности групп (при эффективности новой технологии результаты должны отличаться, и группы продемонстрируют неоднородность).

7. Первоначальную гипотезу будем считать верной, если результаты (например, средний балл) в экспериментальной группе лучше, чем в контрольной, и данный результат подтвержден применением критерия проверки гипотезы.

С одной стороны, применение статистических методов, в частности методов проверки гипотез, предполагает достоверность полученных выводов, их строгое математическое обоснование, с другой стороны, выводы эмпирического исследования могут быть сфальсифицированы или же получены некорректные результаты за счет ошибок, возникающих при неверном понимании основных понятий и методологии исследования.

Учитывая свободу исследователя в выборе методов и интерпретации результатов, необходимо сохранять файлы экспериментальных данных, на основании которых были получены результаты. Для достоверности приведенных результатов необходимо сохранять и быть готовым предоставить весь исходный материал, включая тестовые опросники, результаты контрольных работ и т.д.

Заключение

При использовании методов математической статистики при проведении педагогического эксперимента необходимо четкое понимание инструментария, возможности его применения в каждом конкретном случае.

Так при проверке гипотезы об эффективности новой технологии необходимо прежде всего получить репрезентативные выборки. При проведении эксперимента сделать разбиение учащихся на две группы: в одной из которых занятия проводятся с использованием новой технологий, в другой – проводятся традиционным, ранее используемым способом. Далее необходимо проверить, являются ли выборки однородными. Нельзя проводить исследование на классах с разным уровнем подготовки, классах разной параллели, при сравнении полученных статистических данных. Так, например, будет неверным использование новой технологии в 5-х классах и сравнение результатов с 6-ми классами, где данная технология не была реализована. Также нужно учитывать, что группы должны обладить примерно одинаковым уровнем знаний и сформированных компетенций. В целях подтверждения однородности выборок можно провести тестирование и в контрольной, и в экспериментальной группах и проверить результат, например, используя критерий хи-квадрат.

После того как исследователь убеждается в однородности выборок, возможно проведение эксперимента в течение выбранного исследователем временного интервала. В течение заданного временного интервала педагог реализует новую технологию и по завершении эксперимента проводится итоговое тестирование, позволяющее получить результаты как в контрольной, так и в экспериментальной группах.

Обычно в качестве основной гипотезы формулируется равенство средних значений (среднего балла), а в качестве альтернативной гипотезы берется утверждение, что среднее в экспериментальной группе больше, чем в контрольной. В случае принятия альтернативной гипотезы эффективность применяемой технологии подтверждается экспериментальными данными. По полученным в результате проведения тестирования данным возможна реализация одного из критериев проверки гипотез. Следует заметить, что возможно применение различных критериев, и не следует ограничиваться лишь вышеприведенными вариантами.

Более достоверными будут результаты, полученные при использовании различных критериев, которые рассчитаны на разные типы шкал и разную чувствительность.