Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

Поверхностной энергии в ее анизотропной части и работе испускания электронов из металлов посвящено значительное число работ, поскольку ее необходимо учитывать при решении практических задач, с которыми сталкиваются и техники, и технологи. Так, в микроэлектронике уже используются технологии на наноуровне 14–16 нм, но на заре материалы с размерами 7–10 нм. Для размеров таких материалов характерны совершенно новые физические свойства. В этой области сами объекты начинают проявлять размерную зависимость, и на их свойствах сказывается и ее анизотропия.

В работе [1] методом термодинамики поверхности получены аналитические соотношения для размерной зависимости поверхностной энергии сферической наночастицы, которые в случае малой и большой кривизны у этой частицы соответствуют формулам Толмена и Русанова, а в промежуточной области они отличаются.

В работе [2] автором был разработан метод измерения поверхностной энергии в металлах.

Этот метод дает возможность измерять не только поверхностную энергию, но и диффузионную ползучесть в поверхности металлов, которая оказывается чувствительной к химическому и структурному состоянию поверхности. Суть этого метода заключается в приложении малых нагрузок к фольге или проволочке, а затем нахождении уравновешивающихся сил при растяжении. По существу, этот метод похож на метод «нулевой ползучести», предложенный еще в начале 1930-х гг.

В работе [3] для исследования толщины металлических пленок, где поверхностная энергия играет решающую роль, использовались классическая термодинамика поверхности, электронно-статистическая металлов. Однако вопрос о толщине пленки остается открытым.

В работе [4] методом электронно-статистического расчета поверхностной энергии металлов определен метод оценки для работы выхода электронов из металла со структурами, имеющими гексагональную и ромбическую сингонию.

В работе [5] определена связь поверхностной энергии в ее анизотропной части с кристаллической структурой. Основываясь на экспериментальных исследованиях и теоретических расчетах, показано, что модель, которая названа коротко координационным плавлением кристалла (МКП), связана не только с кристаллической структурой, но и со свойствами ее поверхности.

Начиная с работ Таммана (1920-е гг.), уже 100 лет, измерению поверхностной энергии уделяется большое внимание, особенно в связи с исследованием наноструктур, где роль поверхности является определяющей при изготовлении устройств микро- и наноэлектроники.

В перечисленных выше работах предлагаются различные модели, которые описывают физические свойства поверхности и позволяют вычислять ее поверхностную энергию. Однако вопрос о толщине слоя атомарно-гладких металлов остается открытым, хотя экспериментально этот вопрос уже продвигается. Например, методом рассеяния скользящих рентгеновских лучей определены толщины у золота (1,2 нм) и у кремния (3,1 нм) [6]. То есть они представляют собой наноструктуры.

Настоящая работа является продолжением работы [7], где предлагается эмпирическая модель, которая позволяет рассчитывать не только поверхностную энергию, но и толщину поверхностного слоя металлов. Если к нашей модели применить модель А.И. Русанова, то мы объясняем и анизотропию кристаллических решеток металлов, что и является целью настоящей работы.

Описание эмпирической модели

Нами в работе [7] при рассмотрении температуры плавления малых частиц было получено уравнение

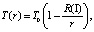(1)

где параметр R(I) определяется выражением

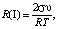(2)

где σ – поверхностное натяжение, υ – молярный объем, R – универсальная газовая постоянная, Т – температура.

Экспериментальные исследования, проведенные нами с физическими объектами на тонких пленках различной природы: механических, оптических, магнитных [8], – а также результаты других исследователей [9] показали размерную зависимость всех физических свойств малых частиц и тонких пленок. Эта зависимость выглядит следующим образом:

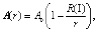(3)

где A(r) – физическое свойство (механическое и т.д.), которое зависит от линейного размера (размерный эффект), А0 – физическое свойство (объемное), которое от размера не зависит.

Ясно, что поверхность твердого тела представляет собой наноструктуру. То же самое относится и к жидкости.

Уравнения (1), (2) и (3) имеют одинаковую структуру и расходятся при r → 0, поэтому доопределим уравнение (3) и запишем окончательно:

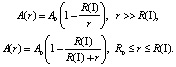(4)

Схема модели показана на рисунке. Она представляет собой идеальный атомарно-гладкий монокристалл без вакансий, дислокаций и других дефектов. Слой R0 называется дебройлевским слоем, и для чистых металлов его толщина находится от 0,1 Å до 1 Å. В слое R0 происходят квантованные размерные процессы. В слое R(I) отмечают коллектив атомов металла и потому их называют внутренними или коллективными явлениями. Размерные эффекты такого типа существуют только в наноструктурах и для металлов составляют от 1 до 7 нм. В этом слое с поверхностными состояниями осуществляется релаксация или реконструкция самой атомной поверхности [6]. Для атомов золота константа кристаллической решетки равна 0,41 нм и релаксация происходит на трех атомных слоях. Такие эффекты проявляются только в наноструктурах.

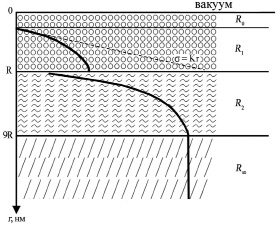
R – слой де Бройля; R1 – слой R(I); R2 – слой R(II); R∞ – слой массивного образца Схема модели показана поверхностного слоя

Толщина слоя R(II) равна ориентировочно R(II) ≈ 9R = R∞ (< 100 нм). Этот слой связан с объемной фазой, и в этом слое протекают размерные процессы, связанные с длиной свободного пробега фононов, электронов, магнонов и другими квазичастицами в твердом теле. Иными словами, этот слой связан с наноструктурой, толщина которой по оценкам многих авторов не превышает 100 нм [9].

Толщина слоя R(I) связана с поверхностной энергией σ соотношением (2). В работе [7] нами установлена связь

σ(Дж/м2) = 10–3∙Tm(K). (5)

Здесь Tm(K) обозначает температуру плавления. Уравнение (5) оказалось справедливым для большинства металлов и для других соединений. Когда положим, что T(K) = Tm(K), то получим

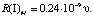(6)

Из формулы (6) следует, что поверхностный слой R(I) зависит лишь от молярного объема искомого элемента, который можно вычислить по известной формуле υ = M/ρ, M – молярная масса (г/моль), ρ – плотность (г/см3).

А.И. Русанов в работе [10] получает следующую линейную зависимость

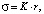(7)

где K – коэффициент пропорциональности, зависящий от температуры и состава фазы (α) (рисунок, слой R(I)).

Проведем сравнение формул (5) и (7):

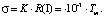(8)

Откуда имеем

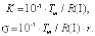(9)

Здесь Tm – температура плавления наноструктуры: υ = M/ρ, M – молярная масса (г/моль), ρ – плотность (г/см3).

Наличие в уравнении (9) координаты r (x, y, z) или r (a, b, c) приводит к анизотропии поверхностного натяжения:

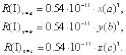(10)

Поверхностная энергия d-элементов

Попробуем использовать полученные выше соотношения (10) для определения поверхностного натяжения d-металлов, для которых эта величина экспериментально определена методом «нулевой ползучести» [11] (табл. 1).

Температуры плавления V, Ta, W, Re, Os (которые лежат больше 3000 К) лучше вычислять при σ = 0.7∙10-3∙Tm. В остальном величина поверхностного натяжения лежит в пределах экспериментальных данных.

Таким образом, эмпирическая модель поверхности твердых тел, основанная на идеях Гиббса (1839–1903), Толмена (1949–1951), Русанова (1967) и наших работ (2018, 2019), неплохо согласуется с экспериментальными данными и позволяет рассчитывать теоретически многие процессы на поверхности твердых тел и в наноструктурах. Здесь особо нужно подчеркнуть заслугу исследователей Кабардино-Балкарского государственного университета им. X.М. Бербекова, которые с 1950-х гг. внесли и теоретический, и экспериментальный вклад в теорию поверхности твердого тела и работы которых мы цитируем постоянно.

Толщина поверхностного слоя кубических d-элементов

Переходные элементы в таблице Д.И. Мен- делеева подразделяют на d-элементы, лантаниды (или 4f-элементы) и актиниды (5f-элементы). Различия между ними обусловлены различием в строении электронных оболочек. Сами d-электроны оказывают сильное влияние на соседние атомы и ионы, предопределяя особую природу химических связей.

В табл. 2 приведена толщина поверхностного слоя d-металлов, рассчитанная по уравнению (6) около температуры плавления (за исключением атомов 7 периода). Все размеры R(I) имеют значения около 2 нм (исключая иттрий и скандий).

В табл. 3 толщина слоя R(I) приведена для лантаноидов.

Здесь наблюдаются значения от 4 нм до 7 нм, что в два раза больше толщин слоя для d-элементов. Именно поэтому f-элементы не образуют высокоэнтропийных сплавов.

Анизотропия поверхностного слоя d-элементов

Учтем теперь уравнения (5) и (9) и рассчитаем толщину поверхностного слоя гексагональных d-элементов, т.е. учтем их анизотропию (табл. 4).

Здесь в скобках приведены значения na = R(I)a/ra, nc = R(I)c/rc (ra, rc – постоянные кристаллических решеток элементов), а na, nc – представляют собой число монослоев поверхностного слоя.

Заключение

В настоящей работе в итоге получено уравнение (6), которое позволяет рассчитывать толщину поверхностного слоя совершенных монокристаллов, что особенно важно при разработке устройств, основанных на наноструктурах. Уравнение (5) позволяет с хорошей точностью рассчитывать поверхностную энергию (поверхностное натяжение) не только металлов, но и других твердых тел. Уравнение (10) позволяет учитывать анизотропию кристаллической структуры металлов, что, несомненно, важно в наноустройствах.

Работа выполнена по программе МОН РК. Гранты № 0118РК000063 и № Ф.0781.