Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

В настоящее время проблемам обработки данных в массивах отводится значительное место во многих прикладных науках. Данное обстоятельство объясняется тем, что от правильной обработки набора данных напрямую зависит конечный результат, и, в случае если изначально данные были интерпретированы и обработаны неверно, исследователь может получить в итоге значительно искаженные данные, что сведет на нет все его усилия.

Как известно, исчерпывающей характеристикой массива случайных данных в различных исследованиях является закон распределения, которому подчиняется данный массив [1]. Однако в прикладных исследованиях закон распределения, как правило, бывает неизвестен или же не определен однозначно [2].

Проблеме идентификации закона распределения с опорой исключительно на массив данных посвящено достаточно большое количество трудов отечественных и зарубежных ученых и отведена большая роль в области теории вероятностей и математической статистики [3].

В рамках поставленной задачи разработано огромное количество различных методов и процедур, среди которых можно выделить следующие: метод гистограмм, приближение сплайнами, корневая оценка плотности, рекуррентная ядерная оценка, интегральная оценка, стохастическая регуляризация, метод проекций, структурная минимизация риска, оценка максимума правдоподобия и т.д. При этом, несмотря на все многообразие подходов к решению задачи идентификации закона распределения, абсолютное большинство методов идентификации закона распределения базируется на его основных особенностях: асимметрии, эксцессе и т.д. [4].

Немаловажным в данном списке является метод оценки тяжести хвостов распределения. При этом широко известно, что значительное количество процедур идентификации законов распределения могут быть достоверно применимы только для распределений, имеющих легкие хвосты [5]. Аналитика массивов данных, которые подчиняются распределениям с тяжелыми хвостами, должна проводиться неклассическими статистическими методами, поскольку имеет место нарушение основного условия Крамера, описывающего производящую функцию моментов [1].

В настоящий момент не существует единого стандарта оценки тяжести хвоста. При этом чаще других используется оценка Хилла [5]. Однако никаких обоснований предпочтений данной оценки, как правило, не приводится. Потому применение данной оценки нуждается в достоверной проверке на различных законах распределения.

Цель исследования: проверить адекватность оценки Хилла для определения тяжести хвоста в различных законах распределения.

Задачи исследования:

– подобрать законы распределения с разной степенью тяжести хвостов;

– оценить тяжесть хвоста при помощи различных методов оценок;

– провести сравнение полученных результатов.

Материалы и методы исследования

Исследования выполнены в лаборатории кафедры управления и информатики в технических системах Оренбургского государственного университета.

В качестве распределений были взяты следующие: равномерное непрерывное; нормальное; Стьюдента; логистическое; Коши. Данные законы являются очень распространенными, а кроме того, обладают сильно различающимися кривыми распределения, поведение которых, безусловно, влияет на конечный результат.

Подбор распределений осуществлялся исходя из тяжести их хвостов; при этом для чистоты эксперимента предпочтения отдавались распределениям, не имеющим асимметрии.

Для определения количества каждого из видов законов распределений в данном исследовании использовалась распространенная формула, взятая из работы В.Н. Дианова «Перспективные направления повышения надежности вычислительной техники и систем управления» [6]:

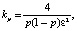(1)

где P – вероятность события, ε – допустимая погрешность вычислений.

Предпочтение данному способу отдано в силу заведомой ненормальности большинства распределений.

Вероятность, как правило, задается на уровне 0,95. Погрешность для данной проверки берется на уровне 0,5, поэтому общее число каждого исследуемого распределения составляло 337.

Для проведения эксперимента на генераторе случайных чисел программы Mathсad 15 были сгенерированы три массива данных (n = 1000), подчиняющихся равномерному (U), нормальному (N), логистическому (log) закону распределения, а также распределению Стьюдента (St) и Коши (С), с такими параметрами, чтобы размах вариации для каждого был примерно одинаков.

Оценка Хилла для исследования тяжести хвоста определялась по следующей формуле:

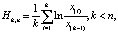(2)

Поскольку данная формула, как приведено в некоторых исследованиях [7], не дает численного результата, то используем уже известную систему преобразований, описанную в работе «Модели оценки параметров телекоммуникационного трафика в автоматизированных информационно-управляющих системах» [8].

Искомая оценка находилась для каждой из квантилей, по результатам чего были построены квантильно-квантильные графики [9]. Затем строилась касательная к полученному графику и вычислялись уравнения регрессии с основой в виде полинома второй степени. Далее через тангенсы угла касательной и оси абсцисс вычислялся искомый параметр, являющейся оценкой тяжести [10].

Данный метод является наиболее универсальным, он описан в большинстве литературных источников и применяется на практике чаще других [11]. Вместе с тем в отечественных и зарубежных трудах нет никаких исследований, отображающих точность и достоверность данного подхода [12]. Однако необходимо отметить, что указанный метод Хилла далеко не единственный, который может быть применен для сравнения хвостовой части изучаемых распределений [13].

В качестве альтернативной оценки использовался метод отношений. Он основывается на том, что с увеличением тяжести хвоста его значения начинают значительно отличаться от среднего. Для реализации этого метода из ранжированного массива данных получают интервальный ряд, который тоже ранжируют. Далее выбирают хвостовую часть, которая составляет, как правило, от 1 % до 20 %.

Результаты исследования и их обсуждение

Для реализации метода отношений хвостовая часть бралась на уровнях 1 %, 3 %, 5 %, 10 %, 15 % и 20 %.

Результаты проверки приведены в табл. 1.

Как видно из представленной таблицы, оценки, полученные различными способами, различаются между собой. Для того чтобы однозначно отделить один закон распределения от другого, необходимо, чтобы интервалы оценок не пересекались, иначе говоря, чтобы максимум оценки одного распределения был меньше минимума другого распределения. Для выявления различий в оценках построим таблицы разностей для каждого из рассматриваемых законов распределений (табл. 2–5).

Как видно из таблицы, ни один из методов не помогает отличить равномерное непрерывное распределение от нормального распределения. Равномерное распределение от распределения Стьюдента можно отличить при помощи оценки Хилла или метода отношений с уровнем 5 %. Равномерное распределение от логистического распределения позволяют отличить методы отношений с уровнями 3 %, 5 %, 10 %, 15 %. Наконец, равномерное непрерывное распределение от распределения Коши можно отличить при помощи любого из перечисленных методов.

Согласно данным таблицы, нормальное распределение можно отличить только от распределения Коши при помощи метода отношений с уровнями 1 %, 3 %, 5 %, а также при помощи оценки Хилла. Остальные описанные случаи не дают возможности различения перечисленных распределений.

Как показывают данные таблицы, распределение Стьюдента также отличается только от распределения Коши при помощи метода отношений с уровнями 1 %, 3 %, 5 %, 10 % или оценки Хилла; все перечисленные виды оценки не помогают отличить распределение Стьюдента от логистического распределения.

Таблица 5

Разности максимума оценки тяжести хвоста логистического распределения с минимумами других распределений

Согласно представленным в таблице данным, логистическое распределение можно отличить от распределения Коши при помощи методов отношений с уровнями 1 %, 3 %, 5 % или оценки Хилла.

Из приведенных выше данных очевидно, что наиболее приемлемым является метод отношений с уровнем 5 %, который позволяет различать наибольшее количество законов распределения из представленного перечня. Данный метод более оптимален, чем оценка Хилла, поскольку с большей точностью позволяет отличать логистическое распределение от равномерного непрерывного распределения.

Заключение

В работе представлен способ идентификации некоторых законов распределения на основе оценки тяжести их хвостов. Выбраны пять законов распределений с различной степенью тяжести хвоста, также выбран ряд оценок, включающий в себя как широко применяемую оценку (оценку Хилла), так и более оригинальные оценки (метод отношений с различным уровнем).

Проведены попарные сравнения законов распределения в зависимости от тяжести хвоста каждым из перечисленных методов, все полученные оценки приведены в соответствующих таблицах.

Полученные разными способами оценки тяжести хвоста сравнивались при помощи метода разниц. Данным способом определено, что наилучший результат в проблеме идентификации закона распределения показывает метод отношений с уровнем 5 %.

Необходимо также отметить, что ни один из методов не выдал гарантированного результата отделения одного закона распределения от другого. Соответственно, для объективизации оценки необходима комбинация указанного метода с каким-либо другим с целью получения более точной и объективной картины распределения исследуемых массивов данных.