Энтропия – это одно из фундаментальных свойств стохастических систем. В настоящее время достаточно распространено использование энтропии для описания поведения открытых стохастических систем в различных областях [1–4]. Общим в этих работах является использование введенной К. Шенноном информационной энтропии [5].
Однако применение информационной энтропии в качестве модели многомерных стохастических систем сталкивается с затруднениями: необходимо оценивать вероятности всех возможных состояний системы (это требует больших объемов выборок, кроме того, некоторые состояния заранее могут быть неизвестны), а также затруднено моделирование взаимосвязей между элементами многомерных систем.
Этих недостатков лишена модель, использующая дифференциальную энтропию [6]. Она основана на представлении системы в виде случайного вектора и разложении его дифференциальной энтропии на компоненты – энтропии хаотичности и самоорганизации. Однако все компоненты вектора должны быть непрерывными случайными величинами. Это существенно сужает область применения энтропийного моделирования, поскольку во многих приложениях, например в медицине, экономике, часто вместо фактических значений признаков используют их сгруппированные величины или вводят их балльные (рейтинговые) оценки [7–9].
В [10] описан частный случай энтропийного моделирования, когда несколько компонент были дискретными случайными величинами. Однако выбор вида закона распределения непрерывной случайной величины, аппроксимирующей дискретную компоненту, недостаточно обоснован. Также не приведено исследование точности энтропийного моделирования при наличии балльных компонент, а также не были учтены особенности смешанного (непрерывного и дискретного) состава компонент случайного вектора.
Целью статьи является описание методики энтропийного моделирования многомерных стохастических систем, все или часть компонент которых являются балльными показателями или получены с помощью группировки, и ее апробация на модельных данных.
Материалы и методы исследования
Представим многомерную стохастическую систему в виде случайного вектора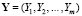 
. Его дифференциальная энтропия равна
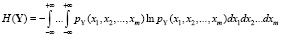, (1)
где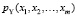 
– плотность распределения случайного вектора Y.
Формула (1) была предложена К. Шенноном в [5] как формальный аналог понятия информационной энтропии для m-мерного непрерывного случайного вектора Y. Эта величина впоследствии А.Н. Колмогоровым совместно с И.М. Гельфандом и А.М. Ягломом была названа дифференциальной энтропией [11].
Предлагаемый подход основан на модели многомерной стохастической системы в виде случайного вектора Y с взаимно зависимыми компонентами, являющимися непрерывными случайными величинами и использует дифференциальную энтропию: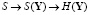 
.
Каждая компонента Yi вектора Y является одномерной случайной величиной, характеризующей функционирование соответствующего элемента системы.
В [6] доказано, что если все компоненты Yi имеют дисперсии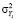 
, то дифференциальная энтропия H(Y) случайного вектора Y равна
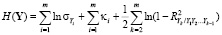, (2)
где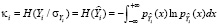 
– энтропийный показатель типа закона распределения случайной величины Yi; 
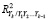– индексы детерминации регрессионных зависимостей. Первые два слагаемых 
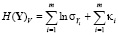названы энтропией хаотичности, а третье 
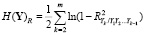– энтропией самоорганизации.
Проблема состоит в том, что все компоненты Yi в (1) должны быть непрерывными случайными величинами, что не позволит определить энтропийные показатели типа их законов распределения. Покажем это. Рассмотрим некоторую дискретную случайную величину Z, имеющую ряд распределения, представленный в табл. 1.
Таблица 1
Ряд распределения случайной величины Z
|
Z |
z1 |
z2 |
z3 |
... |
zn–1 |
zn |
|
pk = P(Z = zk) |
p1 |
p2 |
p3 |
... |
pn–1 |
pn |
Запишем функцию распределения FZ(x) случайной величины Z
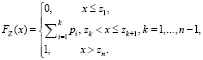
очевидно, что плотность вероятности pZ(x) случайной величины Z всюду, кроме точек zk, равна нулю, а в точках zk не существует, т.е.
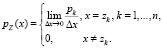
Рассмотрим дифференциальную энтропию дискретной случайной величины Z
.
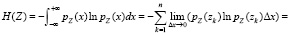
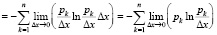Поскольку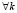 
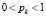и 
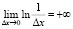, то предел в каждом слагаемом расходится и стремится к 
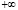. Поэтому дифференциальная энтропия дискретной случайной величины Z не существует (
).
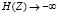Таким образом, при использовании энтропийной модели (1)–(2) все компоненты случайного вектора Y должны быть непрерывными случайными величинами. Если некоторая компонента Yi является дискретной случайной величиной, то ее необходимо заменить на непрерывную. В общем виде это делать нельзя, так как в зависимости от вида непрерывной функции распределения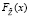 
, аппроксимирующей функцию FZ(x), можно получить практически любое значение энтропии 
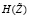, от некоторой константы до любой сколь угодно большой отрицательной величины (с ростом точности аппроксимации). Таким образом, энтропия (1) может использоваться для дискретных случайных величин только, если они получены из непрерывных путем преобразований (группировки, переход к балльным величинам и т.д.). В этом случае для определения необходимо восстановить исходную функцию распределения непрерывной случайной величины Z0, которую заменили дискретной случайной величиной Z. Восстановить истинную функцию 
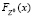невозможно.
Поэтому ограничимся приближенным вариантом применительно к распространенным ситуациям, когда от Z0 к Z переходят с помощью группировки данных и балльных показателей.
Результаты исследования и их обсуждение
Рассмотрим оба этих случая.
Случай 1. Группировки данных. Пусть ряд распределения дискретной случайной величины Z, представленный в табл. 2, получен путем группировки значений некоторой непрерывной случайной величины Z0.
Таблица 2
Ряд распределения случайной величины Z
|
zk |
4 |
8 |
10 |
14 |
19 |
22 |
|
pk = P(Z = zk) |
0,1 |
0,15 |
0,2 |
0,25 |
0,2 |
0,1 |
Обозначим середины всех внутренних интервалов групп как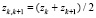 
. Обычно при группировке данных левую границу z0,1 первого интервала и правую границу последнего интервала определяют следующим образом [9]: 
, 
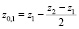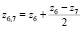. В результате от ряда распределения из табл. 2 перейдем к группировке (табл. 3).
Таблица 3
Группировка для случайной величины Z
|
Группа |
(z0,1, z1,2) |
(z1,2, z2,3) |
(z2,3, z3,4) |
(z3,4, z4,5) |
(z4,5, z5,6) |
(z5,6, z6,7) |
|
(2; 6) |
(6; 9) |
(9; 12) |
(12; 16,5) |
(16,5; 20,5) |
(20,5; 23,5) |
|
|
pk |
0,1 |
0,15 |
0,2 |
0,25 |
0,2 |
0,1 |
Считая, что на каждом интервале некоторая непрерывная случайная величина Y распределена равномерно, с учетом заданных вероятностей pk, достаточно просто восстановить плотность вероятности pY(x): на каждом k-м интервале она будет постоянна и равна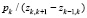 
. На рисунке приведен график плотности вероятности pY(x).
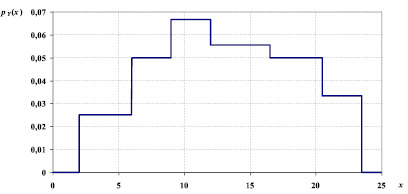
График плотности вероятности pY(x)
В общем случае для ряда распределения из табл. 1 аппроксимирующая плотность вероятности непрерывной случайной величины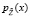 
будет равна
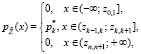(3)
где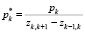 
, 
, 
, 
, 
.
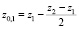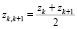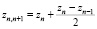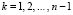Теперь вычисляем оценку дифференциальной энтропии распределения (3) по формуле
.
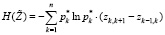Случай 2. Балльные показатели. Пусть исследуемая непрерывная случайная величина Z0 была в результате некоторых преобразований заменена на ряд балльных показателей (для определенности считаем баллы от 1 до M) (табл. 4).
Таблица 4
Ряд распределения балльной случайной величины Z
|
Z |
1 |
2 |
3 |
... |
M–1 |
M |
|
pk = P(Z = k) |
p1 |
p2 |
p3 |
... |
pM–1 |
pM |
Очевидно, что это частный случай рассмотренного выше случая группировок, если приравнять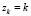 
, 
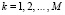. Тогда вместо (3) получим формулу для аппроксимирующей плотности вероятности непрерывной случайной величины 
:
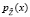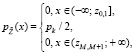
где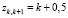 
, 
.
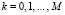Пример. Сгенерируем выборку из стандартного нормального распределения Z0 объема 100 чисел. Выборочное среднее квадратичное отклонение оказалось равным s = 0,9278. Дифференциальная энтропия равна [12]
.
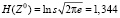Теперь сгруппируем данные на 7 интервалов (табл. 5). Ширина интервала каждой группы оказалась равной D = 0,59.
Таблица 5
Группировка для выборки из 100 наблюдений
|
(z0,1, z1,2) |
(z1,2, z2,3) |
(z2,3, z3,4) |
(z3,4, z4,5) |
|
(-2,19; -1,6) |
(-16; -1,01) |
(-1,01; -0,42) |
(-0,42; 0,17) |
|
p1 = 0,06 |
p2 = 0,13 |
p3 = 0,18 |
p4 = 0,16 |
|
(z4,5, z5,6) |
(z5,6, z6,7) |
(z5,6, z6,7) |
– |
|
(0,17; 0,76) |
(0,76; 1,35) |
(1,35; 1,94) |
– |
|
p5 = 0,29 |
p6 = 0,12 |
p7 = 0,06 |
– |
Дифференциальная энтропия для распределения, задаваемого табл. 5, равна
.
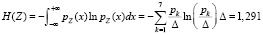Разница между величинами H(Z) и H(Z0) составила менее 4 %, что говорит о достаточно точной оценке дифференциальной энтропии.
Выводы
Показано, что дифференциальная энтропия не может использоваться при моделировании дискретных случайных величин.
Для случаев, когда дискретные случайные величины получаются в результате группирования данных или перехода к балльным показателям, возможно использование дифференциальной энтропии. Это достигается за счет перехода от дискретных случайных величин к их аппроксимациям непрерывными случайными величинами, имеющими кусочно-линейные функции распределения.
Описана методика энтропийного моделирования многомерных стохастических систем, все или часть компонент которых являются балльными показателями или получены с помощью группировки.
Работа выполнена при финансовой поддержке гранта РФФИ, проект № 20-51-00001.