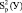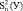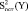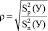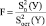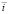Исследование путей повышения экономической эффективности улучшения транспортно-эксплуатационных показателей лесовозных автомобильных дорог основывается на изучении закономерностей, отражающих влияние элементов дороги на основной транспортно-эксплуатационный показатель – скорость движения.
Поэтому дальнейшее повышение эффективности совершенствования принципов и методов обоснования оптимальных скоростей требует существенного развития и продолжения изысканий по поиску новых, эффективных решений по этому вопросу.
Цель работы заключается в исследовании скоростей движения лесовозного подвижного состава в зависимости от скорости потока, состава, интенсивности движения, ширины проезжей части и характера продольного профиля участков дорог.
Материалы и методы исследования
Выбрать необходимое количество участков дорог с необходимыми параметрами для проведения эксперимента представляется затруднительным, поскольку эти участки должны варьироваться по четырём признакам и одновременно отвечать ряду требований с целью компенсации посторонних влияний. Поэтому экспериментальные работы были разделены на два самостоятельных направления, в результате осуществления которых должна быть получена общая зависимость.
Первое направление обуславливается необходимостью определения зависимости скоростей от ширины проезжей части, интенсивности и состава движения, второе – от характеристик продольного профиля.
1. Измерения скоростей движения лесовозного подвижного состава с целью определения зависимости от ширины проезжей части, интенсивности движения и состава потоков производились на специально выбранных участках лесовозных автомобильных дорог.
Для ликвидации посторонних воздействий на режим движения выбирались участки дорог, не имеющие продольных уклонов, горизонтальных кривых, съездов, переездов, близко расположенных сооружений и других факторов, вызывающих снижение скорости.
Длина экспериментальных участков, отвечающих указанным требованиям, назначалась около 500 м в обе стороны от места установки регистрирующего прибора.
За единицу наблюдения принят один час с определенной интенсивностью движения. Количество часов наблюдения для каждой ширины проезжей части определялось по известной формуле [1–3]:
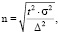 (1)
(1)
где t – функция доверительной вероятности;
σ – среднее квадратическое отклонение, определяющееся из предварительных на- блюдений;
∆ – необходимая точность наблюдения.
Размах выборки средних скоростей не превышал 20 км/час.
Общее количество часов наблюдений и диапазон интенсивности движения отражен на рис. 1.
Общее количество автомобилей составило 3175, количество часов наблюдения 60. По причине определенных трудностей, встречающихся при выборе участков дорог с различной шириной проезжей части и с сопоставимыми значениями интенсивностей движения, совокупность экспериментальных данных характеризовалась различием средних уровней интенсивности движения по ширине проезжей части. Это обстоятельство учитывалось при обработке и анализе экспериментальных данных.
2. Формирование выборки для определения зависимости снижения средних скоростей автомобилей от распределения проектных продольных уклонов характеризуется необходимостью включения в исследование возможно большего диапазона сложности продольного профиля.
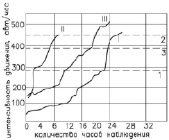
Рис. 1. Диапазоны и средние уровни интенсивностей движения, охваченные экспериментом
Для наблюдений были выбраны участки дорог, характерные для районов с пересеченным рельефом местности. Распределение уклонов экспериментальных участков представлено на рис. 2.
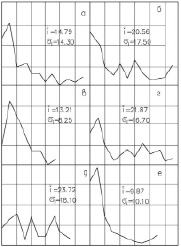
Рис. 2. Распределение уклонов экспериментальных участков лесовозных автомобильных дорог
Экспериментальные исследования и за- меры производились при интенсивности движения до 17 авт./час, что соответствует свободным условиям движения [3–5].
Выбор автомобилей для исследования изменения скоростей на участке определялся необходимостью внесения в выборку основных скоростных групп. Скоростные группы включали следующие типы автомобилей:
1. Легковые, микроавтобусы.
2. Грузовые, легковые, средние и автобусы.
3. Лесовозы, грузовые тяжёлые, средние с прицепами.
На каждом из участков обследовалось равное количество представителей разных скоростных групп.
При анализе результатов измерения скоростей на горизонтальных участках имелась в виду линейная связь между средней скоростью потока, интенсивностью и составом движения при различной ширине проезжей части. Это предположение подтверждается проведёнными исследованиями Курьянова В.К., Кондрашовой Е.В., Скрыпникова А.В. и др. [6–8] и некоторыми зарубежными исследователями [9–11].
В процессе регистрации скоростей автомобилей обработка позволила непосредственно получить распределение скоростей по длине участков и их статистические характеристики.
Установление характера процесса при пассивном эксперименте не является однозначной задачей, и выборке может соответствовать большое количество математических моделей. Кроме того, графическое определение формы связи в случае множественной корреляции затруднено, поэтому математическое выражение связей производится в результате проверки нескольких гипотез.
В данном случае выдвинуто 3 гипотезы о виде регрессии.
В общем виде уравнение выразится:
1. У = 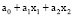 ; (2)
; (2)
2. У = 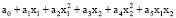 ; (3)
; (3)
3. У = 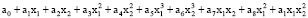 . (4)
. (4)
Таким образом, предполагается подбор аппроксимирующей зависимости путем последовательного повышения степени полинома с сохранением линейного характера уравнения относительно коэффициентов регрессии.
Аппроксимация эмпирических данных по уравнениям (2)–(4) произведена с помощью стандартных компьютерных программ. В результате получены коэффициенты уравнений регрессии, приведенные в табл. 1.
Таблица 1
Коэффициенты уравнений регрессии
|
а0 |
а1 |
а2 |
а3 |
а4 |
а5 |
а6 |
а7 |
а8 |
а9 |
|
0,88032 |
0,01281 |
0,00260 |
- |
- |
- |
- |
- |
- |
- |
|
1,08145 |
-0,00291 |
0,00029 |
0,00446 |
0,00014 |
0,00042 |
- |
- |
- |
- |
|
1,23690 |
-0,06489 |
0,02976 |
0,00458 |
0,00055 |
0,00014 |
0,00010 |
0,00350 |
0,00030 |
0,00028 |
Далее производился статистический анализ уравнений регрессии, в результате которого должна быть подтверждена одна из гипотез о форме связи [11].
Первый этап анализа состоит в оценке дисперсий.
1. Вычисляется дисперсия линии регрессии, характеризующая изменчивость зависимой переменной в результате изменения независимых переменных:
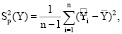 (5)
(5)
где 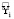 – теоретические значения зависимой переменной;
– теоретические значения зависимой переменной;
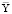 – общая средняя зависимой переменной;
– общая средняя зависимой переменной;
n – 1 – число степеней свободы выборки.
2. Определяется средний квадрат (полная дисперсия) зависимой переменной:
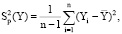 (6)
(6)
где Yi – выборочные значения зависимой переменной.
3. Вычисляется остаточная дисперсия, отражающая рассеивание экспериментальных точек относительно линии регрессии:
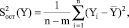 (7)
(7)
где m – число коэффициентов регрессии.
После оценки дисперсии определяется теснота связи зависимой переменной с независимой переменной с независимыми, при помощи корреляционного отношения:
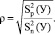 (8)
(8)
Окончательный выбор уравнения регрессии осуществлялся при проверке адекватности гипотетических математических моделей эмпирической выборки. Проверка адекватности производится оцениванием соотношения дисперсий при помощи F–критерия Фишера. Оценивалась случайность отклонения эмпирических данных от линии регрессии при заданном уровне значимости.
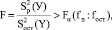 (9)
(9)
где α = 0,05 – уровень значимости;
fn = n – 1 – число степеней свободы полной дисперсии;
fост = m – 1 – число степеней свободы остаточной дисперсии;
Fα(fn:fост) – табличное значение критерия для заданных уровней значимости и числа степеней свободы дисперсий.
Если выполняется соотношение (9), то долю остаточной дисперсии по отношению к полной можно считать несущественной и гипотеза верна. И, наконец, для выбранного уравнения регрессии необходимо определить доверительные границы, т.к. результат вычисления по корреляционному уравнению может не совпадать с Уфак. В данном случае можно говорить только о точном определении границ, в которых с заданной вероятностью заключается Уфак.
Для ρ = 0,95 Уфак = 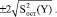 (10)
(10)
Результаты статистического анализа гипотезы представлены в табл. 2.
Таблица 2
Результаты статистического анализа гипотезы
|
|
|
|
|
|
fn |
fост |
f0,005 |
|
0,01761 |
0,00853 |
0,02792 |
0,675 |
1,308 |
82 |
2 |
3,012 |
|
0,02193 |
0,03853 |
0,01701 |
0,706 |
2,265 |
82 |
0,5 |
2,34 |
|
0,02334 |
0,03853 |
0,01707 |
0,780 |
2,265 |
82 |
9 |
2,03 |
Сопоставляя характеристики тесноты связи и степени адекватности, видим, что гипотеза 3 наиболее хорошо описывает эмпирическую выборку.
Следовательно, принимается гипотеза 3, по которой величина τ выражается полиномом 3-й степени:
τ = 1,23 – 0,0649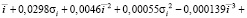
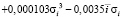 + 0,000304
+ 0,000304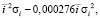 (11)
(11)
где 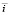 и σi – статистические характеристики продольного профиля.
и σi – статистические характеристики продольного профиля.
Дальнейшая обработка экспериментальных данных заключалась в объединении в общей зависимости формул (7)–(9) с целью вывода расчетной формулы, отражающей влияние геометрических параметров дороги на среднюю скорость автомобильного потока.
В общем виде зависимости выразятся следующим образом:
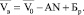 (12)
(12)
С некоторым приближением сумму 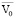 + Бр можно принять скоростью свободного движения потока на горизонтальном участке дороги. Коэффициент τ выражает снижение скорости свободного движения потока на участках с продольными уклонами, отличными от 0. Следовательно,
+ Бр можно принять скоростью свободного движения потока на горизонтальном участке дороги. Коэффициент τ выражает снижение скорости свободного движения потока на участках с продольными уклонами, отличными от 0. Следовательно, 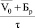 представляет собой скорость свободного движения автомобильного потока на таких участках.
представляет собой скорость свободного движения автомобильного потока на таких участках.
С учетом (12) скорость потока определится как:
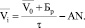 (13)
(13)
Уравнение (13) предполагает, что увеличение интенсивности движения на участках со сложными продольными профилями не вызывает дополнительного снижения скорости и снижение скорости по мере увеличения параметров 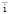 и σi происходит одинаково для любой ширины проезжей части. Это обстоятельство несколько углубляет оценку режима движения автомобильного потока, но подобный подход допустим при технико-экономических обоснованиях, характеризующихся высокой устойчивостью решений и поэтому не требующих определения влияния побочных воздействий на скорость движения. Следует заметить, что опытное определение указанного влияния требует проведения достаточно сложного, желательно активного эксперимента.
и σi происходит одинаково для любой ширины проезжей части. Это обстоятельство несколько углубляет оценку режима движения автомобильного потока, но подобный подход допустим при технико-экономических обоснованиях, характеризующихся высокой устойчивостью решений и поэтому не требующих определения влияния побочных воздействий на скорость движения. Следует заметить, что опытное определение указанного влияния требует проведения достаточно сложного, желательно активного эксперимента.
На основании выражений (7)–(9) и (13) скорость движения автомобильного потока с учетом воздействия продольного профиля определится для ширины проезжей части 7,5 следующим образом:
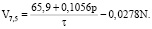 (14)
(14)
С целью проверки полученных экспериментальным путем зависимостей произведен сравнительный анализ формул с зависимостями Кероглу Л.А. [11] и данными непосредственных измерений скоростей, не вошедших в исходные выборки (табл. 3), что характеризует сравнение скоростей, вычисленных и измеренных на горизонтальных участках лесовозных автомобильных дорог.
Таблица 3
Сравнение скоростей, вычисленных и измеренных на горизонтальных участках лесовозных автомобильных дорог
|
N |
p |
b |
V по данным Кероглу |
V по данным СибАДИ |
V фактическая |
|
71 |
20 |
7 |
55,62 |
66,06 |
61,90 |
|
98 |
27,3 |
7 |
54,76 |
66,03 |
65,3 |
|
138 |
18,5 |
7 |
53,64 |
64,04 |
63,50 |
|
202 |
39,4 |
7 |
61,66 |
64,30 |
65,10 |
|
243 |
32,4 |
7 |
50,42 |
62,40 |
61,60 |
|
459 |
23,2 |
7 |
44,11 |
55,56 |
57,40 |
|
493 |
21,4 |
7 |
43,07 |
54,30 |
55,80 |
|
148 |
28 |
2х7,5 |
53,90 |
70,40 |
68,00 |
|
172 |
27,9 |
2х7,5 |
53,31 |
70,03 |
67,20 |
|
370 |
24,7 |
2х7,5 |
48,47 |
66,82 |
64,80 |
|
485 |
24,9 |
2х7,5 |
45,69 |
65,07 |
66,80 |
|
420 |
24,3 |
2х7,5 |
47,20 |
65,90 |
67,10 |
Значительные расхождения результатов расчета скоростей по данным Кероглу Л.А. с наблюденными и вычисленными по формулам (8), (9) объясняются повышением динамических качеств автомобилей, когда проводились исследования [11]. Кроме того, формулы (8), (9) выведены на основании выборок, включающих интенсивности движения несколько меньшие, чем использовались Кероглу Л.А. Проведенный анализ подтверждает необходимость проведения эксперимента по наблюдению изменения скорости движения в зависимости от ширины проезжей части.
Измерения скоростей производились на участках с характерными распределениями продольных уклонов, поэтому анализ полученных зависимостей произведен только для этого типа лесовозных автомобильных дорог. Для анализа из общей совокупности данных взяты случайные единицы наблюдений.
Табл. 4 отражает исходные данные для вычисления скоростей движения и полученных результатов.
Таблица 4
Вычисления скоростей движения
|
|
σi |
р % |
τ2(р) |
α(р) |
N авт./4 |
V расч. |
V факт. |
|
21,87 |
16,7 |
32,7 |
0,775 |
0,0140 |
174 |
55,56 |
56,59 |
|
14,79 |
14,3 |
29,0 |
0,770 |
0,0142 |
50 |
63,21 |
62,50 |
|
20,56 |
17,5 |
21,0 |
0,750 |
0,0160 |
50 |
58,41 |
58,33 |
|
16,21 |
10,25 |
35,4 |
0,78 |
0,0136 |
100 |
63,32 |
56,84 |
|
9,5 |
7,5 |
16,2 |
0,710 |
0,0164 |
210 |
60,00 |
61,86 |
|
14,79 |
14,3 |
14,4 |
0,700 |
0,017 |
97 |
60,40 |
58,33 |
|
21,87 |
16,7 |
44,4 |
0,790 |
0,0125 |
126 |
58,10 |
69,84 |
|
21,87 |
16,7 |
25,2 |
0,760 |
0,0152 |
111 |
56,92 |
59,32 |
|
9,87 |
10,1 |
35,6 |
0,780 |
0,0136 |
124 |
63,76 |
67,83 |
|
23,72 |
18,1 |
29,7 |
0,770 |
0,0144 |
118 |
55,12 |
57,71 |
|
23,72 |
18,1 |
38,7 |
0,780 |
0,013 |
125 |
56,82 |
57,26 |
Анализ небольшой выборки показывает, что вычисленные значения скоростей хорошо сходятся с наблюденными среднечасовыми скоростями. Среднее расхождение при этом S = 2,4 км/час.
Таким образом, использование зависимостей (12), (14) при решении задач технико-экономического обоснования является достаточно обоснованным.
Выводы
Проведение экспериментальных работ и результаты обработки полученной информации позволяют сделать следующие выводы.
1. Скорость движения автомобилей является одной из важных характеристик, по которой можно оценивать степень влияния параметров лесовозной автомобильной дороги на экономические показатели её работы. В результате экспериментального изучения влияния ширины проезжей части, интенсивности и состава автомобильного потока на его скорость получены расчетные формулы, дающие возможность определить с известной погрешностью скорость потока как функцию от N, в и р. Эти зависимости при сравнительных расчётах дали результаты, значительно лучше сходящиеся с фактическими скоростями, чем результаты, полученные по данным других исследований.
2. Существенное влияние на скорость автомобильного потока оказывает сложность продольного профиля. Экспериментальным путём выведен коэффициент, учитывающий снижение скорости автомобильного потока в зависимости от характеристик 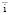 и σi. Этот коэффициент выражается полиномом третьей степени и предполагает учет снижения скорости свободного движения.
и σi. Этот коэффициент выражается полиномом третьей степени и предполагает учет снижения скорости свободного движения.
3. В результате анализа зависимостей V = f(N, b, p) и коэффициента 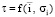 получены уравнения, выражающие скорость автомобильного потока как функцию геометрических параметров дороги, интенсивности и состава движения.
получены уравнения, выражающие скорость автомобильного потока как функцию геометрических параметров дороги, интенсивности и состава движения.
Формализация связи V = f(N, b, p, 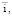 σi) позволяет учесть влияние этих параметров дороги и автомобильного потока на элементы целевой функции, отражающие транспортно-эксплуатационные расходы.
σi) позволяет учесть влияние этих параметров дороги и автомобильного потока на элементы целевой функции, отражающие транспортно-эксплуатационные расходы.