1. Обзор
Чтобы обнаружить и идентифицировать объект на изображении, необходимо выделить особенности этого объекта и сравнить их с признаками, извлеченными из областей на основном изображении. Поскольку структура изображения представляет собой матрицу пикселей со значениями цвета (R, G, B), обработка изображения также является матричной. Свертка матрицы изображения с разными матрицами фильтров обладает различными свойствами. После каждой свертки формируется слой (англ. layer) в процессе работы. После извлечения всех функций происходит процесс категоризации, в результате которого будут созданы функции, которые будут соответствовать какому-либо слою объекта.
Цель данной статьи – описать проблему обнаружения и идентификации объектов на изображениях/ видео. Объясните математические основы метода в моделях, таких как свертка, функции объединения, функции активации, функции потерь. Затем дайте общую модель сети CNN [1] для проблем и как реализовать эту модель в инструменте программирования с двумя фазами обучения и прогнозирования. Иллюстративный пример – это рукописная задача идентификации из 10 цифр с набором данных образца изображения MNIST [2].
2. Проблема идентификации образца на изображениях
Проблема распознавания образцов на изображении может быть выражена следующим образом: Для образца «o» и изображения «I». Пожалуйста, укажите на изображении «I», есть ли образец «о»? Если да, то насколько это точно?
Если это связано с реальным временем, обработка для ответа на вышеуказанный вопрос должна обеспечивать время для представления кадров и место для хранения.
Для простоты выражения модель проблемы распознавания образов, используемая в этой статье, представляет собой задачу «распознавания рукописных чисел» с 10 числами в образцах изображений.
3. Математическая теория обработки изображений
3.1. Операторная свертка при обработ- ке изображений
Обнаружение объекта на изображении – это обработка изображения для выделения области изображения, содержащей узор. Затем матрица изображения будет преобразована на основе математических операций для извлечения областей изображения, содержащих особенности образца. Одна из самых распространенных операций – свертка.
Если есть матрица I (размер wx×wy) и матрица F (размер kx×ky), то свертка обозначается ⨂, матрица C = I ⨂ F вычисляется по следующей формуле:
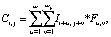 (1)
(1)
где {i = 1÷(wx – kx + 1), j = 1÷(wy – ky + 1)} или размер матрицы C(xc, yc) с xc = wx – kx + 1 and yc = wy – ky + 1) (рис. 1).
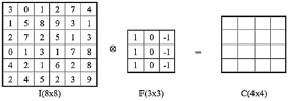
Рис. 1. Данные для сверточной иллюстрации
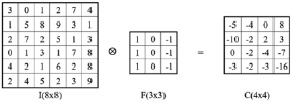
Рис. 2. Иллюстрация результатов умножения свертки
Конкретный случай со значением ячейки результата C [1,1] будет рассчитан следующим образом: C[1,1] = I[1,1]×F[1,1] + + I[1,2]×F[1,2] + I[1,3]×F[1,3] + I[2,1]×F[2,1] + + I[2,2]×F[2,2] + I[2,3]×F[2,3] + I[3,1]×F[3,1] + + I[3,2]×F[3,2] + I[3,3]×F[3,3] = -5.
Продолжаем вычислять таким образом, чтобы матрица F покрывала все пиксели матрицы I. Окончательный результат изображен на рис. 2.
При применении фактической матрицы пикселей, если изображение монохромное, матрица изображения I будет иметь один слой. Если изображение является цветным, матрица изображения I представлена тремя слоями матрицы, соответствующими трем цветам (R, G, B), отсюда матрица C также представлена тремя соответствующими слоями (рис. 3).
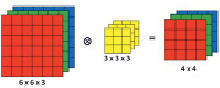
Рис. 3. Иллюстрация с несколькими слоями умножения свертки

Рис. 4. Иллюстрация результата с помощью различных матриц фильтров
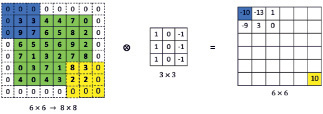
Рис. 5. Примененное заполнение p = 1 перед сверточным с матричного фильтра 3×3
Матрица F имеет значение «матрицы фильтра», в результате чего получается новая матрица изображения с более выделенными свойствами. С каждым разным значением матрицы фильтра F получаются разные результаты C-матрицы, как показано на рис. 4 [3], «Original» – исходное изображение, «Gaussian Blur» – изображение размытое (плавное), «Sharpen» – изображение выделяется линиями, «Edge Detection» – изображение разделяется краями.
3.2. Данный метод сохраняет размер получаемой матрицы
Поскольку матрица фильтра F меньше по размеру, чем матрица изображения I, размер результирующей матрицы C также меньше, чем размер матрицы I, что означает, что результирующая матрица потеряла часть своей информации о краях справа и снизу матрицы I. Чтобы сохранить размер матрицы C относительно матрицы I, перед выполнением сверточного произведения мы добавляем в матрицу I ячейки со значениями 0 на 4 краях, количество строк (столбцов) смещения это называется значением заполнения «p» (англ. padding). Рис. 5 соответствует p = 1, а матрица C также имеет тот же размер, что и матрица I(6×6).
Легко понять, что при заполнении p = 1 добавляются 2 строки и 2 столбца. Следовательно, размер общей матрицы C равен (xc = wx + 2p – kx + 1, yc = wy + 2p – ky + 1).
3.3. Метод добавления шага для уве- личения скорости свертки
При начальном умножении свертки после вычисления значения ячейки в матрице C матрица F перемещается влево (или вниз) на столбец (строку) по сравнению с матрицей «I». Другими словами, 's' (шагов) равно 1. Чтобы увеличить скорость вычислений, мы можем увеличить количество прыжков выше. (До тех пор, пока размер матрицы фильтра размера F-ядра не будет превышен. Так как если есть еще ячейки, пропускаемые матрицей I, то они не включаются в расчет свертки.) Если число прыжков больше 1, размер полученной матрицы C будет уменьшаться с соответствующим числом раз.
Формула для расчета размера матрицы C(xc, yc) в общем случае будет иметь вид
xc = 1 + (wx + 2p – kx)/s;
yc = 1 + (wy + 2p – ky)/s. (2)
Если матрица I изображения и матрица F фильтра являются квадратными (wx = wy = w и kx = ky = k), формула для расчета размера матрицы C будет иметь вид
xc = yc = 1+ (w + 2p – k)/s. (3)
3.4. Метод уменьшения размера полу- чаемой матрицы
Во многих случаях, когда размер матрицы «I» является большим, а размер матрицы фильтра «F» мал, размер матрицы «С» будет также большим. Соседние ячейки имеют одинаковое или как минимум не сильно различающееся значение. Далее, для извлечения характеристик изображения, требуется сохранить пиксели, обладающие значительными особенностями. Это означает, что размер матрицы «С» будет значительно уменьшен (понижающая выборка), что таким образом увеличит скорость умножения на следующих этапах. Эта операция называется «объединение/ пулинг» (англ. pooling).
Квадрат, содержащий ячейки, объединенные в матрицу C, называется маской. Эмпирическое правило обычно заключается в том, чтобы брать «средний пул» или «максимальный пул» (рис. 6).
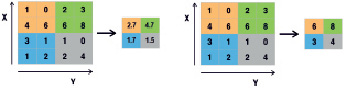
Рис. 6. Операции «средний пул» и «самый большой пул» с «прыжком», равным 2
Легко определить правильное количество сокращений размера по количеству шагов. Обычно это значение p = {2, 4, 8, ...}.
4. Проблемы машинного обучения и рас- познавания образцов
4.1. Обзор машинного обучения
Существует два довольно четких определения машинного обучения:
Согласно Артуру Самуэлю (1959), машинное обучение – это дисциплина, позволяющая компьютерам учиться без предшествующего этому программирования их на обучение [4].
По словам профессора Тома Митчелла из Университета Карнеги-Меллона, «машинное обучение» – это компьютерная программа, которая предполагает учиться на опыте E, выполняя задачи T и измеряя производительность P. Если ее производительность применима к T задач и измеряются увеличением в значении параметра P, из опыта E [5].
Распознавание образов – это индустрия машинного обучения. Другими словами, это можно рассматривать как «необходимость оказывать влияние на необработанные данные, специфическое воздействие которых будет зависеть от их типа» [6]. Как таковой, он представляет собой набор методов обучения с визуальным контролем.
Проблема распознавания образцов имеет две фазы: «Обучение» (англ. training) и «Предиктивная идентификация» (англ. prediction/ recognition).
Этап обучения существует для того, чтобы иметь возможность идентифицировать образцы, до этого систему необходимо обучить с помощью существующих и маркированных вручную моделей. Программа прочтет данные множества образцов, выяснит правила расчета, чтобы можно было с определенной точностью присвоить значение метке. Чем больше количество исследуемых образцов, тем выше точность. Параметры, включенные в расчет, называются «весами» (англ. weight), функция расчета отклонения от метки называется «функцией потерь» (англ. loss funtion), коэффициент компенсации потерь называется «смещением» (англ. bias).
На этапе прогнозирования (распознавания) система считывает данные выборки, передает их через набор вычислений и сравнивает их с обученными данными и назначается метке, которая имеет лучшую точность в наборе данных, независимо от того, обучена ли она.
Из статьи [7] известно, что «с машинным обучением инженеры никогда не знают правильных решений, но компьютеры способны справиться с этой задачей». Нейронные сети представляются темными и непостижимыми, другими словами, являют собой «черный ящик». Это означает, что проблема улучшения ограничена, и зачастую трудно понять, почему система улучшается или как ее можно улучшить. В системе машинного обучения просто нет инструмента для фильтрации алгоритма. С чистым машинным обучением единственное, что в данной ситуации возможно – это испробовать множество различных алгоритмов. К сожалению, это не гарантирует, что вы улучшите результаты и достигнете необходимой точности.
Если будут обнаружены какие-либо ошибки или систему необходимо исправить по какой-либо другой причине, процесс возвращается к исходной точке. Таким образом, нам необходимо уточнить модель сети CNN, реорганизовать набор обучающих данных и запустить обучение с нуля.
4.2. Расчетная модель для задачи рас- познавания образов в картинках
4.2.1. Введение
Для задачи распознавания образов в изображении с характеристикой «x» (xi с i = 1÷N), обозначенным «y» (yi с i = 1÷M), на основе матрицы фильтра «w». При подобных характеристиках появляется вопрос о том, в какой форме будет функция прогнозирования y = f(x)?
Реляционной моделью между входными данными является изображение «x», а выходными данными, обозначенными «y», является следующая линейная функция:
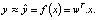 (4)
(4)
В этой формуле: матрица wT – называемый вектор коэффициента (или весовой вектор), нам нужно найти, y – реальное значение, 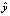 – прогнозируемое значение.
– прогнозируемое значение.
4.2.2. Построение и оптимизация функ- ции потерь
4.2.2.1. Ошибка прогноза
После того, как мы разработали модель прогнозирования выхода, такую как (4.1), нам нужно найти оценку, соответствующую задаче. Для общей задачи регрессии мы ожидаем, что разница e между фактическим значением y и прогнозируемым значением 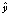 минимальна, или
минимальна, или 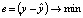 . Другими словами, мы хотим, чтобы следующее значение было как можно меньше:
. Другими словами, мы хотим, чтобы следующее значение было как можно меньше:
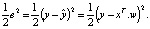 (5)
(5)
Здесь мы берем квадрат, потому что е может быть отрицательным. Наименьшую ошибку можно описать, взяв абсолютное значение 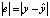 , но этот метод используется редко, поскольку функция абсолютного значения вообще не является дифференциальной, что неудобно для оптимального использования в дальнейшем. Коэффициент
, но этот метод используется редко, поскольку функция абсолютного значения вообще не является дифференциальной, что неудобно для оптимального использования в дальнейшем. Коэффициент 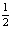 позже будет убран при получении производной от e по параметру модели w.
позже будет убран при получении производной от e по параметру модели w.
4.2.2.2. Коэффициент компенсации сме- щения bias
Обратите внимание, что отношение 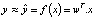 является линейным, для удобства при вычислении мы добавляем свободный термин, называемый «коэффициент компенсации» (англ. bias):
является линейным, для удобства при вычислении мы добавляем свободный термин, называемый «коэффициент компенсации» (англ. bias):
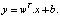 (6)
(6)
Эту величину также можно узнать во время обучения – вектор коэффициентов «w».
4.2.2.3. Функции потери
В машинном обучении и математической оптимизации функции потерь для классификации – это выполнимые в вычислительном отношении функции потерь, представляющие собой цену, заплаченную за неточность прогнозов в задачах классификации (проблема определения того, к какому конкретному типу наблюдения какой тип относится) [8].
То же самое происходит для всех пар (вход, выход) 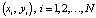 , где N – количество наблюдаемых выборок. Нам нужно усреднить наименьшую ошибку – эквивалентно нахождению модели (функции)
, где N – количество наблюдаемых выборок. Нам нужно усреднить наименьшую ошибку – эквивалентно нахождению модели (функции) 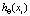 (с приведенным выше анализом
(с приведенным выше анализом 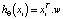 ), чтобы следующая функция достигла минимального значения (MSE – минимальный квадрат ошибки):
), чтобы следующая функция достигла минимального значения (MSE – минимальный квадрат ошибки):
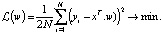 (7)
(7)
Функция представляет собой функцию квадрата, достигающую минимума в точке минимума, или производная функции будет равна 0. Найденное решение w является решением уравнения
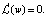 (8)
(8)
В математической теории непрерывность может быть вычислена.
На деле существует множество формул для функций потерь:
– Функция средне-квадратической ошибки (MSE) или «среднее квадратическое отклонение» (MSD), как в формуле (7).
– Функция абсолютного значения (очень полезна в статистике):
+ Стандартное отклонение:
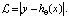 (9)
(9)
+ Среднее абсолютное отклонение:
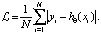 (10)
(10)
+ Максимальное абсолютное отклонение:
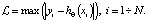 (11)
(11)
– Функция классификации вероятности: при условии 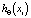 задает значение [0÷1], это означает, что способность xi относится к классу X. Если выбрано значение ≥ 0,5, то оно также удаляется в противном случае. Функция потерь выглядит следующим образом:
задает значение [0÷1], это означает, что способность xi относится к классу X. Если выбрано значение ≥ 0,5, то оно также удаляется в противном случае. Функция потерь выглядит следующим образом:
+ Логарифмическая потеря [9]:
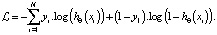 (12)
(12)
4.2.2.4. Функции активации
«Функция активации» (англ. activation function) – это функция, оценивающая степень результата, полученного после свертки. Если порог пройден, новая примененная матрица фильтра (ядро – англ. kernel) считается приемлемой. В сетевой модели CNN (описывается далее) функция активации имитирует скорость передачи аксона нейрона. Ниже приведены некоторые типичные функции активации и их родственные графические иллюстрации, которые обычно используются в задаче определения шаблонов на фотографиях / видео (рис. 7). Подробнее [9].
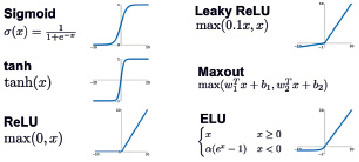
Рис. 7. Некоторые типичные функции активации
5. Модель сети CNN для задачи рас- познавания образцов
Выше были описаны: свертка (англ. convolution), ядро (англ. kernel), шаг (англ. stride), добавленная матрица (англ. padding), пул (англ. pooling), весовая матрица (англ. weight matrix), параметры смещения (англ. bias), функции активации и функция потерь. Далее описывается распространенная модель сети CNN для проблем распознавания объектов на фотографиях.
5.1. Общая модель CNN
Для правильного функционирования распознавания образов следует основывать его на его ключевых особенностях. Чтобы правильно представить эти свойства, нам нужно полагаться на их параметры. Наша цель – научить машинное обучение этим параметрам с помощью множества этапов тестирования и оценки. Исследуемая модель использует два процесса: «распространение» (англ. propagation) и «обратное распространение» (англ. backpropagation). Общая модель CNN представлена на рис. 8 [1].
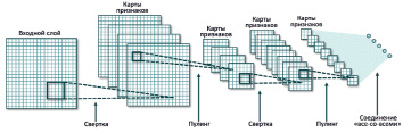
Рис. 8. Общая модель свертки нейронной сети CNN
CNN состоят из двух компонентов.
Скрытые слои или извлечение объектов: в этой части сеть выполнит серию сверточных вычислений и объединение для обнаружения объектов. Например, если имеется изображение зебры, в этом разделе сеть распознает её полосы, уши и четыре ноги.
Слои классификации: в этом разделе класс с полными ассоциациями действует как классификатор ранее извлеченных объектов. Этот слой показывает вероятность появления объекта на изображении.
5.2. Процесс обучения
Процесс обучения будет проходить следующим образом. Цель состоит в том, чтобы включить предварительно назначенные обучающие образцы. Проблема состоит в том, чтобы вычислить матрицу фильтра (англ. kernel) и матрицу весов, используя матрицу входного изображения для вычисления доступных меток (или значение вероятности с существующей меткой примет наибольшее значение).
Процесс прогрессивного распространения. Для каждой матрицы входного изображения после умножения свертки на матрицу фильтрации (случайно сгенерированную матрицу) применение триггерной функции, функции агрегации (при её наличии) и соответствующих параметров приведет к получению искомой матрицы и отсюда к новым результатам. Весь процесс объединен в один слой (англ. layer). Количество выходных матриц каждого слоя будет равно количеству матриц фильтра, каждая фильтрующая матрица будет представлять атрибут для извлечения. Наиболее часто используемой триггерной функцией является ReLU.
Если в модели есть дополнительные слои, выполните то же, что описано выше. Выходной сигнал после прохождения этих слоев представляет собой набор 2-мерных матриц (которые рассматриваются как матричный блок тензорного потока). Значения матрицы фильтра (kernel) и параметры смещения будут временно сохранены (рис. 9) [10–12].
Далее следуют полностью подключенные слои (англ. fully connected layers/densse) для классификации выборки в соответствии с назначенной меткой. Как рассчитать генерацию взвешенных матриц? Перед входом в этот слой матрицы сглаживаются, что означает их преобразование в векторы (одномерные массивы – англ. one-dimensional arrays). Тогда все еще применяя сверточное умножение с матрицей, преобразованная матрица будет называться весовой с параметрами смещения. Обратите внимание, что матрицы генерируются случайным образом с размерами матрицы, указанными разработчиком. Функция триггера ReLU по-прежнему часто используется.
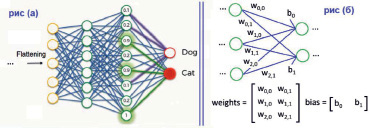
Рис. 9. Иллюстрации полностью связанных слоев
В зависимости от разработчика сети CNN существует много «полностью связанных слоев». И принадлежность к последнему классу определяется в зависимости от того, какие вероятности вернут себе самую высокую соответствующую метку. Завершение процесса «Распространение прогресса». Посмотрите на рис. 5.2.a – иллюстрация вероятности входного предсказания с меткой «кошка – cat», являющейся максимумом с двумя случаями значения 0,9 и одним значением случая 1,0.
Если возвращаемое значение не является самой высокой вероятностью для данной метки, будет выполнен процесс «обратного распространения». Начиная с метки, коэффициент компенсации смещения корректируется таким образом, чтобы значение вероятности, соответствующее данной метке, было наибольшим, далее пересчитываются весовые коэффициенты и т.д. Точно так же весовые коэффициенты, а также параметры смещения обновляются и распространяются обратно до конца слоя «сверточных слоев» (англ. convolution layers) или обратно на слой матрицы входного изображения.
Этот процесс распространения реализуется, в общем, обновляя матрицу фильтра (англ. kernel), смещение параметра (англ. bias) и матрицу весов (англ. weights). Это требуется, чтобы процесс распространения вернулся до наибольшего значения вероятности для метки и обратное распространение также возвращало значение матрицы, соответствующее входной матрице. Поэтому продолжительность фазы обучения часто увеличивается, как показано на рис. 10 [13]. (Обновленные данные в 2015 г.).
Вы можете увидеть больше параметров процесса обучения, упомянутых в таблицах документа [14], и увидеть их иллюстрированную демонстрацию в данном документе [15]. Результатом процесса обучения является файл, содержащий сохраняемые ядра, весовые коэффициенты и параметры смещения, а также путь процесса обучения для идентификации образцов (документов, часто именуемых предварительно обученными файлами или моделью – англ. pre-trained model).
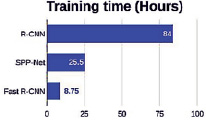
Рис. 10. Сравнение времени обучения между алгоритмами
5.3. Предиктивный процесс иденти- фикации объектов
Когда необходимо идентифицировать объект на изображении, на входе будет распознанное изображение, а на выходе будет значение вероятности, соответствующее метке, назначенной объекту, содержащемуся в изображении. Сеть CNN будет действовать скачкообразно в течение процесса обучения. То есть из входного изображения она будет проходить по «встроенному» пути (известные ядра, смещения, веса), через слои свертки, сглаживать и полностью соединять слои изображения. Наконец, значение ее вероятности равно выходной метке. Потому что следование «пути» происходит только один раз, поэтому данный процесс занимает достаточно короткое время для своего завершения. Ранее с помощью алгоритма R-CNN [16] в 2014 г. распознавание изображения могло занимать 47 секунд. Но теперь с алгоритмом YOLO v5 [17, 18] идентификация изображения может занять всего 2,1 мини-секунды – это является лучшим результатом.
5.4. Создание модели CNN для рас- познавания рукописных цифр
Проблема распознавания рукописного ввода: если введенное изображение в оттенках серого имеет размер 28×28 пикселей. Выходом является значение вероятности, соответствующее числовой метке в пределах 0÷9 (рис. 11) [2].

Рис. 11. Пример рукописных цифр, извлеченных из данных MNIST с соответствующим именем файла
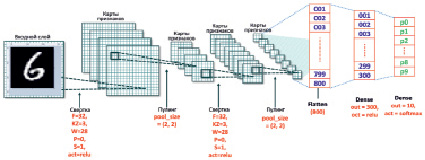
Рис. 12. Дизайн модели CNN распознает рукописные цифры
5.4.1. Построение модели CNN для про- блемы
Модель CNN спроектирована следующим образом: для простоты и чтобы не потерять общности, модель спроектирована с двумя «сверточными» слоями, включая пул, один сплющенный и два полностью соединительных слоя (англ. fully connected layers/ denses). Выводом является значение вероятности результата для 10 случаев, соответствующих меткам чисел 0÷9 (рис. 12).
Объяснение параметров:
- со слоем свертки: f = количеству фильтров, KZ = размеру фильтра, w = размеру входной матрицы, p = количеству добавленных строк (англ. padding), s = шагу (англ. stride), act = имени триггерной функции (англ. activation function).
- С классом пула: pool_size = объединенному размеру лица (англ. pooling size).
- Выровненный слой: после прохождения двух слоев convo и pool размер матрицы будет 5×5 и после умножения с 32 фильтрами, ее значение будет равно 800.
- Первый полностью подключенный слой Dense (англ. fully connected layer): выходной параметр устанавливается равным 300, это установлено на опытных испытаниях, потому что размер входной матрицы составляет 28×28 = 784 пикселей. Но важно, что таким образом количество пикселей в области изображения почерка составляет не более 50 % от общего количества пикселей. Триггерной функцией здесь является ReLU.
- Второй полностью связанный слой Dense (также конечный слой): выходной параметр устанавливается равным 10, это необходимо, потому что прогнозируемый номер класса составляет 10 цифр. Функция триггера – softmax, поскольку дает результат, согласно которому вероятность вычисления для соответствующей метки pi является значением вероятности для i-й метки (i = 0÷9).
Значения параметров задаются пользователем на основании опыта проведенных результатов испытаний несколько раз.
Код модели в Python, использующий бэкэнд – это «tensorflow» и функции класса «keras» [6] (рис. 13).
Результаты запуска программы (рис. 14).

Рис. 13. Код для моделирования CNN на Python с использованием keras
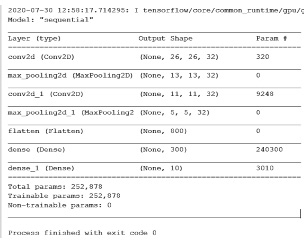
Рис. 14. Результат при запуске команды, суммирующей параметры модели CNN
Объяснение количества обученных параметров в соответствии с результатом рис. 5.7, показанным выше.
Вход первого класса Convo представляет собой матрицу. После выхода из первого слоя свертки размер матрицы составляет 26×26, и таких матриц 32 (соответствует 32 фильтрам). Количество обучаемых параметров составляет (3×3)×32 + 32 (смещение) = 320.
Вне первого класса пула матрицы уменьшены в размере до 13×13, и таких матриц 32. Количество дополнительных тренировочных параметров равно 0.
Таким образом, вход второго слоя свертки составляет 32 матрицы.
Из второго класса convo, поскольку имеется 32 входных матрицы, размер фильтра равен 3×3 = 9, количество матриц фильтра равно 32 и 32 дополнительным смещениям, поэтому число обучаемых параметров равно 32×(3×3)×32 + 32 = 9248.
Размер матриц уменьшается до 11×11, после прохождения второго слоя пула с размером пула = (2, 2) размер матрицы будет 5×5. Дополнительные параметры не обучаются.
Вход первого плотного слоя – 800 числовых значений. Поскольку выходной сигнал установлен на 300, количество обученных параметров составляет 800×300 + 300 (смещение) = 240300.
Вход второго (а также последнего) класса Dense составляет 300 числовых значений. Поскольку выходной сигнал установлен на 10, количество обученных параметров составляет 300×10 + 10 (смещение) = 3010.
Общее количество параметров для обучения составляет: 320 + 9248 + 240300 + + 3010 = 252878.
Переменная модели хранит данные построенной нами модели.
5.4.2. Проведение тренировочного про- цесса
Это стандартный пример задачи: количество входных изображений и метка, уже встроенная в базу данных MNIST [2, 15].
Делается декларация для загрузки данных изображений из MNIST и назначаются данные для учебных и тестовых наборов. Где 'x' хранит матрицу изображения, а 'y' – назначенную метку (рис. 15).

Рис. 15. Код выполнения разделяет наборы данных для обучения и тестирования

Рис. 16. Код нормализует формат набора обучающих данных
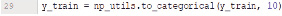
Рис. 17. Код нормализует данные метки обучающего набора

Рис. 18. Код процесса обучения и сохранение в файл данных
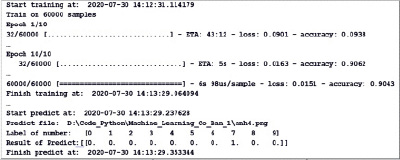
Рис. 19. Результаты (сокращены) при запуске программы
Чтобы ввести данные в тренинг (используя функцию «train» в библиотеке «tenorflow.keras»), необходимо стандартизировать набор данных в формате функции train. В частности, нам нужно следующее (рис. 16).
x_train.shape[0] – количество образцов изображений включено в тренинг (28×28) – размер фотографии; 1 – количество цветовых каналов (поскольку это серое изображение, цветовой канал равен 1). Необходимо преобразовать значение матрицы изображений в обучающие и действительные числа. Каждый пиксель будет иметь серую шкалу от 0÷255, но при возврате значение вероятности составляет всего 0,0÷1,0. Следовательно, необходимо преобразование изображения в градациях серого в значение 0,0÷1,0, что и делает 25-е установление.
Преобразуйте соответствующую матрицу меток y_train, установленную в «один хост-вектор», что означает, что вектор имеет вид: [p0, p1, p2, p3, p4, p5, p6, p7, p8, p9], соответствующий вероятности изображения присваивается с метками 0÷9 (рис. 17).
Далее нужно сконфигурировать функцию компиляции, установить функцию «потери», отобразить «точность» при тренировке и проведите тренировку с количеством повторений с набором данных эпох = 10 раз. И напишите обучающий файл с именем «model_10numbers.h5» (рис. 18).
Результат при запуске программы с набором данных составляет 60000 образцов изображений, повторенных 10 раз, результаты обучения и прогнозы будут следующими (обратите внимание, на рис. 19 изображение содержимого представляет собой комбинацию результатов при запуске программы).
Анализируя результаты, мы видим: изначально значение функции было довольно большим, потеря 0,0901, а точность была низкой 0,0938. Но, в конце концов, при переходе к 10-й итерации (Epoch 10/10) конечный результат – потеря = 0,0151 и точность = 0,9107.
Возвращаясь к рис. 19, входное изображение имеет изображение, аналогичное числу «7», и прогнозируемый результат равен 1,0 = 100 %.
Выводы
Сверточная нейронная сеть CNN – очень полезная модель в проблеме распознавания. Хотя предлагаемое время по своей длительности не является большим, с быстрым развитием информационных технологий сегодня и с участием многих исследователей открываются множества сообществ разработчиков открытого исходного кода. Данные алгоритмы развиваются и улучшаются на протяжении всего времени своего существования. Результаты исследований также передаются многим людям для дальнейших экспериментов и их проверки. Модель CNN установлена на платформе tenorflow с библиотекой keras с простым кодом, результаты его работы интуитивно понятны и просты для понимания. В этой статье также кратко представлена модель CNN и объясняются параметры и процесс реализации. Хорошая реализация диаграммы полностью зависит от идеи разработчика (то есть вашей) и экспериментальных результатов работы с наборами данных, опубликованными в интернете в огромных количествах [19].



