В отечественной практике проектирования трассы лесовозной автомобильной дороги принят метод расчета, который был также широко распространен и за рубежом до массового внедрения автоматизированных методов проектирования. Этот метод основан на расчете закруглений вида клотоида – круговая, кривая – клотоида или клотоида – клотоида, вписываемых в углы тангентального полигона, обычно прокладываемого на местности.
Особенностями применяемых в настоящее время методов сглаживания эскизной линии трассы лесовозной автомобильной дороги является то, что из графического проекта берется такое количество данных, чтобы последовательность элементов трассы и их геометрические характеристики устанавливались однозначно, т.е. чтобы не было неопределённостей при аналитическом расчете трассы [1–3]. Вместе с тем, учитывая значительную трудоемкость этапа графической проработки трассы, в последние годы ведутся исследования методов проектирования, позволяющих облегчить его. В работах [3, 4] предлагается отказаться от концепции однозначного решения геометрии трассы, а из графического решения проекта брать больше координат точек, чем это необходимо для однозначного ее определения.
Цель работы заключается в исследовании методов сглаживания эскизной линии трассы лесовозной автомобильной дороги для получения исходного приближения при последующей аппроксимации трассы клотоидами, круговыми кривыми и прямыми.
Проектируемая ось определяется по методу наименьших квадратов с соблюдением условия заданных допусков отклонения проектируемой трассы от заданных точек.
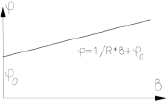
В работе [5] трасса представлена в виде последовательности круговых кривых, клотоид и прямых. С целью анализа линии, нарисованной от руки, рассчитывается и автоматически вычерчивается ее угловая диаграмма, т.е. графическое изображение, на котором в прямоугольной системе координат по оси абсцисс откладывается длина линии (В) от начала рассматриваемого участка, а по оси ординат – угол наклона касательной в соответствующей точке к оси абсцисс в общей системе координат (φ). Угловая диаграмма эскизной линии аппроксимируется угловой диаграммой допустимых трассировочных элементов и, таким образом, осуществляется выравнивание эскизной линии последовательностью отдельных элементов трассы. Выравнивание на угловой диаграмме проще осуществить, чем выравнивание на оригинале. Так, клотоиду, которая на оригинале не может быть представлена явным аналитическим выражением в прямоугольных координатах, на угловой диаграмме легко описать уравнением параболы, круговую кривую – уравнением наклонной, прямую – линией, параллельной оси абсцисс (таблица).
Диаграммы элементов трассы
|
Тип элемента |
Угловая диаграмма |
Диаграмма кривизны |
|
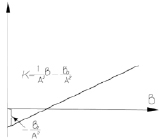
Прямая |
|
|
|
Круговая кривая |
|
|
|
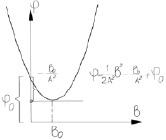
Клотоида |
|
|
Анализируя угловую диаграмму совместно с намеченной трассой, проектировщик разбивает трассу на последовательность элементов (клотоид, круговых кривых и прямых) и намечает их ориентировочные границы, определяя тем самым приближенные геометрические характеристики элементов трассы. По установленным границам последовательности элементов и в зависимости от их вида с помощью уравнительного исчисления определяются геометрические характеристики элементов трассы, из условия, что выбранные границы сохраняются неизменными.
Поскольку, однако, эти границы были установлены на глаз, то возможно, что при изменении границ участков можно достигнуть лучшего выравнивания угловой диаграммы эскизной линии прямыми и параболами. В качестве критерия выравнивания принята сумма квадратов отклонений точек эскизной линии от трассы.
Оптимизация осуществляется итерационным методом. Сначала первая главная точка смещается на величину (Δb) влево и вправо при сохранении всех остальных и регистрируются соответствующие значения критерия. Эта процедура повторяется для второй и каждой последующей точки при сохранении всех остальных в исходном положении. После выполнения этой операции устанавливают, какая из главных точек имеет наибольшее изменение критерия. Для нее смещают границу участка в сторону, соответствующую уменьшению критерия, и отыскивают положение этой границы, при котором достигается наилучшее сглаживание эскизной линии. Положение соответствующей границы уже не меняется на последующих этапах итерационного расчета.
После снова осуществляют поочередное смещение главных точек (за исключением оптимизированной на предыдущем шаге), и та точка, которая на этот раз имеет максимальное изменение критерия, подвергается оптимизации, как на первом шаге. Таким образом, устанавливается положение всех главных точек. Следует отметить, что данный метод оптимизации, основанный на идеях релаксации, не гарантирует нахождение глобального минимума целевой функции. Кроме того, он не позволяет учитывать ограничения на геометрические характеристики элементов, вследствие чего получаемая в результате расчета трасса может не отвечать нормативным требованиям или соответствующим рекомендациям.
Эти недостатки в значительной степени устранены в методе, изложенном в работе Р. Клумпа [5], представляющем собой развитие работ [6–8], где рассматриваются методы программы, с помощью которых эскизная линия раскладывается на проектные элементы трассы (круговые кривые, клотоиды и прямые) аналитическим путем. С помощью программы 1 для точек эскизной линии, заданной координатами последовательности точек, рассчитывается и изображается графически не только угловая диаграмма, но и диаграмма кривизны. Под диаграммой кривизны линии понимают графическое изображение, на котором по абсциссе откладывается длина линии, а по ординате – кривизна. Анализируя эти диаграммы и эскизную линию, устанавливают последовательность и ориентировочные границы проектных элементов трассы. Особенно легко это выполнить с помощью диаграммы кривизны, поскольку проектные элементы трассы на ней представлены простыми линейными зависимостями: клотоиды – наклонными прямыми, круговые кривые – прямыми, параллельными оси абсцисс (рисунок).
С целью облегчения выделения элементов трассы программой 1 предусмотрено два этапа сглаживания диаграммы кривизны эскизной линии кусочно-линейной зависимостью.
С помощью программы 2 диаграмма кривизны эскизной линии выравнивается посредством непрерывной последовательности прямых.
Выравнивание может быть осуществлено в двух вариантах:
1) положение главных точек трассы задано фиксированным;
2) положение главных точек переменное, с помощью чего трасса может быть рассчитана с применением либо метода уравнительного исчисления, либо метода Хилдрета и Д’Эзопе [8]. В работе показано, что в случае больших систем со многими линейно-зависимыми уравнениями, то есть при значительном превышении числа задаваемых точек эскизной линии над количеством переменных, трудно, а зачастую и невозможно найти решение с помощью метода уравнительного исчисления путем многократных итераций с изменением веса точек эскизной линии по определенному закону. Поэтому рекомендуется применять в этих случаях оптимизационный метод. Приведенное ниже описание программы 3 относится только к оптимизационному методу, как более совершенному. В качестве переменных могут быть приняты следующие характеристики трассы:
- центральные углы и радиусы круговых кривых;
- длины прямых;
- параметры клотоид;
- координаты начальной точки и начальное направление оси.
В качестве ограничений могут быть заданы:
– для определенных точек эскизной линии: а) максимально допустимые расстояния от точки до оси; б) максимальные допуски на изменение координат точки; в) проектные углы наклона касательных в общей системе координат и максимальные допуски на отклонение от этих величин;
- минимально допустимые радиусы элементов;
- минимально допустимые параметры клотоид;
- минимально и максимально допустимые соотношения радиусов и параметров смежных элементов.
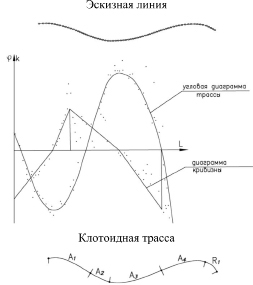
Сглаживание эскизной линии с использованием угловой диаграммы и диаграммы кривизны
Анализ методов проектирования трассы, изложенных в работах [8–10], показывает, что идея, безусловно, прогрессивна и открывает широкие возможности автоматизации проектирования трассы в плане. Однако в рассмотренных методах имеются следующие принципиальные недостатки:
1. Проектирование каждого варианта трассы осуществляется в несколько этапов, что не позволяет существенно сократить сроки и трудоемкость работ.
2. Математические модели целевой функции построены, исходя из предположения, что расстояние между задаваемыми точками эскизной линии приблизительно одинаковое, а изменение угла наклона касательной в смежных точках эскизной линии незначительно.
3. Хотя в принципе параметры клотоид и могут быть приняты в качестве переменных, но сходимость метода в этом случае не обеспечивается, поэтому в работах [11, 12] не рекомендуется использовать параметры клотоид в качестве переменных. Это также ограничивает возможность рассматриваемого метода.
Инженер В. Калогеро предложил метод полиноминального трассирования [8].
Основные положения этого метода следующие:
Задаются:
1) упорядоченное множество контрольных точек
G = {Gili = 1.2,…l},
где Gi = (xi, yi, wi, ti, ui);
xi, yi – координаты i-й контрольной точки;
wi – вес i-й точки, для которой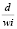 
является максимально допустимым отклонением данной точки от трассы (d – задаваемая константа);
ti – направление касательной в i-й точке;
ui – весовая характеристика для возможности фиксации направления касательной;
2) d – константа, в совокупности с wi устанавливающая допустимое отклонение i-й точки от трассы;
3) rmin – минимально допустимый радиус;
4) У0’, У0» – первая и вторая производные в начальной точке полинома.
Новое множество точек Q определяется следующим образом: k – произвольное число новых точек, отстоящих друг от друга на равном расстоянии, по прямой, соединяющей точки Gi и Gi + 1,
L = l + (l – 1)k,
I = {i + (i – 1)kli = 1.2,…l},
Q = {Qilj = 1,2,…L},
Qj = (Xj, Yj, Wj, Tj, Uj). (1)
Трасса на участке данного множества представляется в виде полинома:
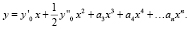(2)
Степень полинома n и его коэффициенты а3, а4,…аn принимаются такими, чтобы трасса удовлетворяла следующим условиям:
а) отклонение от трассы для каждой точки Gi должно быть меньше допустимого:
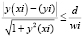; (3)
б) радиус в каждой точке Qi должен быть не меньше допустимого:
|rj| = rmin,
; (4)
в) должно быть минимально выражение
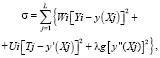(5)
где g – функция веса;
λ – переменная, принимаемая из условия минимизации – n (степень полинома);
k, W, U и g – были определены автором при помощи экспериментов, а λ– определяется программным путем.
Характеристики n, а3, а4,…аn определяются следующим образом: для различных значений λ и для возрастающих значений n решается система линейных уравнений:
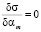, m = 3,4…n, (6)
до тех пор, пока не будет получено удовлетворительное решение.
В методе В. Калогеро [8] предусмотрена возможность задания промежуточных и конечных точек, для которых:
а) фиксированы координаты хi, yi (путем задания максимально большого веса точки, то есть wi);
б) фиксировано направление касательной к трассе ti (путем введения максимально большого значения ui);
в) фиксирована величина радиуса.
Анализ метода полиномиального трассирования:
1. Величина изменения центробежного ускорения не контролируется данным методом. Используя метод полиномиального трассирования в изложенной выше постановке, трудно вносить коррективы в полученные проектные решения.
2. Если наносить контрольные точки трассы, руководствуясь главным образом экономическими соображениями и не прорабатывать ее графически, то трасса может получиться излишне извилистой, что является недопустимым.
3. При использовании полиномиального трассирования осложняется вынос трассы на местность.
Выводы
Подводя итог, можно сделать вывод, что для окончательного трассирования применение на этапе предварительной проработки трассы лесовозной автомобильной дороги методов сглаживания, с использованием полиномов или для получения приближения при последующей аппроксимации трассы круговыми кривыми, клотоидами и прямыми, в полной мере нельзя применять.