Современный мир характеризуется стремительным развитием технологий, в том числе технологий информационного противоборства. Одной из задач конкурирующих систем является взлом каналов радиосвязи и доступ к конфиденциальной информации соперника. Военные ведомства сосредотачивают усилия на разработке и совершенствовании средств радиоэлектронной разведки и радиоэлектронной борьбы. Коммерческие и государственные корпорации регулярно увеличивают затраты на информационную безопасность, защиту от кибернетических атак и сохранность конфиденциальной информации. Однако данная проблема не перестает затрагивать мирную жизнь. Совершенствование методов, способов и средств радиоэлектронной разведки оставляет актуальной задачу защиты информации, передаваемой по радиоканалам, от несанкционированного доступа.
Одним из способов защиты систем радиосвязи от взлома является повышение их скрытности за счёт использования сверхширокополосных сигналов. Это позволяет скрыть от противника сам факт радиопередачи, что делает невозможным применение в отношении системы радиосвязи методов взлома.
Поскольку технические возможности средств радиоэлектронной разведки зачастую неизвестны, то для достижения указанного выше эффекта необходимо стремиться к максимальной скрытности системы радиосвязи [1].
Эта характеристика системы радиосвязи в большей степени зависит от формы и параметров её радиочастотного спектра. Большей скрытностью обладают радиосистемы, спектр сигналов которых равномерно распределён в широком диапазоне частот. Отсутствие энергетических «всплесков» на общем радиочастотном фоне затрудняет обнаружение радиосистемы средствами радиоэлектронной разведки.
Поэтому для количественной оценки скрытности систем радиосвязи, в частности использующих сверхширокополосные сигналы, предлагается использовать показатель равномерности радиочастотного спектра [2].
Известно, что радиосигнал обладает наибольшей скрытностью, если его энергия равномерно распределена в заданном диапазоне частот [3]. То есть для достижения максимального значения данной характеристики спектр сигнала должен быть максимально равномерно распределён в заданной полосе частот, ограниченной выделенным для системы радиосвязи ресурсом радиочастотного спектра.
При равномерном спектре сигнала все гармоники используются с максимальной мощностью, и выявить из общего фона участки с повышенной (пониженной) энергией, учитывая конечные технические возможности средств радиоэлектронной разведки, становится проблематично [4]. Следовательно, усложняется задача обнаружения факта работы системы радиосвязи и организации информационного или энергетического воздействия на неё.
Целью статьи является описание математической модели показателя равномерности радиочастотного спектра сверхширокополосного сигнала, обеспечивающей рост скрытности систем радиосвязи за счёт обоснованного выбора формы используемых сигналов.
Материалы и методы исследования
Для решения задачи количественной оценки скрытности систем радиосвязи на основе анализа степени равномерности их радиочастотного спектра необходимо решить задачу сведения функции (спектра) к показателю. Показатель скрытности должен достигать максимума в случае, когда спектр сигналов системы радиосвязи максимально равномерно распределён в заданной полосе частот, т.е. имеет форму прямоугольника. В то же время минимальное значение показателя скрытности будет иметь любой идеализированный гармонический сигнал, спектр которого имеет ярко выраженный всплеск на конкретной частоте.
Разработку математической модели начнём с формулировки задачи в общем виде. Для этого представим функцию, описывающую радиочастотный спектр, в виде
K = F[G(jω)], (1)
где K – показатель максимальной скрытности;
F[G(jω)] – функционал преобразования функции в показатель.
Функционал (1) представляет собой переменную величину, которая зависит от вида функции, описывающей радиочастотный спектр исследуемого сигнала. Значения амплитудных составляющих радиочастотного спектра, как правило, отличаются. То есть радиочастотный спектр может иметь участки с понижением энергии (выпуклая сверху функция) и участки с повышением энергии (выпуклая снизу функция), соответственно, при получении целевой функции используем неравенство Иенсена
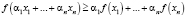, (2)
где y = f(x) – функция, выпуклая на некотором интервале;
х1, х2, …, хn – произвольные числа из этого интервала;
α1, α2, …, αn – произвольные положительные числа, сумма которых равна единице.
Докажем, что рассмотренное неравенство справедливо для любой выпуклой функции.
Под выпуклой функцией f(x) будем понимать функцию, для которой выполняется условие
f′(x) > 0.
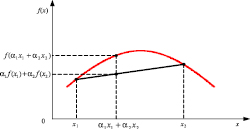
Рис. 1. Геометрический смысл теоремы Иенсена для n = 2
Условимся, что функция y = f(x) выпуклая на некотором интервале (рис. 1), х1, х2, …, хn – произвольные числа из этого интервала, α1, α2, …, αn – произвольные положительные числа, у которых сумма равна единице.
Для доказательства используем понятие полной (математической) индукции.
Пусть А(n) – зависящее от n∈N утверждение. Если доказано, что А(1) выполняется и при условии, что А(n) справедливо для некоторого n, верно также A(n + 1) (шаг индукции), то А(n) справедливо для всех n∈N.
Для n = 2 выражение (2) примет вид
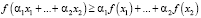. (3)
Геометрически выражение (3) представлено на рис. 1.
Как показано на рис. 1, прямая, образованная точками x1, x2, лежит ниже графика функции f(x), а значит, выполняется (2).
Зададим в качестве базы индукции выражение (3).
Проведём индукционный переход. Для этого воспользуемся индуктивным предположением, поскольку (2) справедливо для n = 2, значит, справедливо и для n – 1, т.е. имеем
.
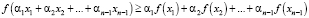Рассмотрим случай n – переменных:
.
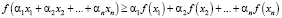Поскольку
,
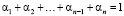то
,
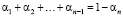т.е.
,
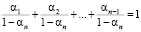тогда
;
.
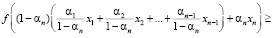
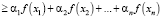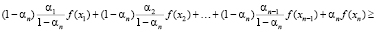
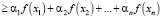Что и требовалось доказать.
С помощью неравенства Иенсена докажем, что выпуклая функция принимает максимальное значение в случае равенства переменных х1, х2, …, хn, т.е.
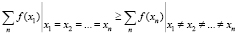. (4)
Пусть
α1 = α2 = … = αn.
Так как
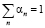, (5)
то
.
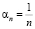Если
х1 = х2 = … = хn (6)
и
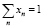, (7)
то
.
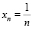В качестве исходного выражения имеем
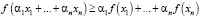. (8)
С учётом (5) и (6) выражение (8) примет вид
;
;
;
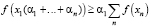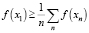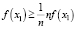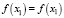. (9)
Из (9) следует, что при х1 = х2 = … = хn функция f(x) принимает максимальное значение.
Рассмотрим случай, когда
х1 ≠ х2 ≠ … ≠ хn; α1 = α2 = … = αn,
тогда выражение (8) примет вид
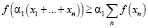. (10)
С учётом (7) выражение (10) можно записать в виде
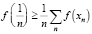. (11)
Из выражения (11) видно, что в случае, когда х1 ≠ х2 ≠ … ≠ хn, функция f(x) может принимать значения меньше максимального f (1/n).
Из данного доказательства и выражений (9) и (11) можно сделать вывод, что
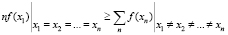. (12)
А значит, утверждение (4) верно. Что и требовалось доказать.
Результаты исследования и их обсуждение
Представленное выше доказательство показывает, что функционал вида (3) может быть применим для вычисления степени равномерности спектра. В случае если все гармоники в спектре сигнала покажут сходные амплитуды (вариант, при котором исполняется условие (7)), функционал вида (12) получит максимально возможное значение.
,
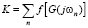где f[G(jω)] – выпуклая функция.
Перейдём к интегральной форме записи неравенства Иенсена (для непрерывного спектра) [5]:
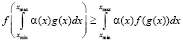; (13)
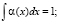
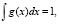(14)
где g(x) и α(x) – функции, которые удовлетворяют условию (14) и определённы в промежутке от xmin до xmax [6].
Учитывая (13), показатель (12) представим в следующем виде:
,
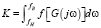где fв – верхняя частота и fн – нижняя частота в полосе частот, выделенной для сверхширокополосной системы радиосвязи.
В научных трудах Л. Больцмана и Дж.К. Максвелла, результаты которых представлены в литературе по теории информации [5], доказано, что энтропия имеет максимальное значение (15), когда состояния системы (возможности) равновероятны.
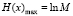. (15)
Энтропией системы называется сумма произведений вероятностей различных состояний системы на логарифмы этих вероятностей, взятая с противоположным знаком
,
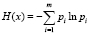где m – число состояний системы (возможностей);
pi – вероятность i-го состояния (возможности).
Для получения показателя с аналогией в теории информации, используем в качестве выпуклой функцию вида
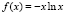. (16)
С учётом (16) математическая модель показателя равномерности радиочастотного спектра сверхширокополосного сигнала будет иметь вид
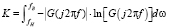. (17)
Значения показателя равномерности радиочастотного спектра сверхширокополосных сигналов
|
Название генератора (тип сигнала) |
Значение показателя равномерности спектра сигнала с учётом радиочастотной маски РФ, % |
|
PD-0.04 (моноимпульс Гаусса) |
50,1 |
|
TMG (отрицательной полярности) |
61,6 |
|
TMG (положительной полярности) |
74,2 |
|
TMG (радиоимпульс) |
75,3 |
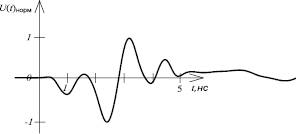
Рис. 2. Синтезированный радиоимпульс
В результате моделирования с использованием разработанной математической модели (17) и программы [7] получены значения показателя равномерности радиочастотного спектра сверхширокополосных сигналов некоторых генераторов, приведённые в таблице. Моделирование проводилось в сравнении с идеализированным сигналом, имеющим спектр прямоугольной формы (значение показателя равномерности 100 %).
В целях достижения максимального значения показателя равномерности и повышения скрытности системы радиосвязи синтезирован радиоимпульс, форма которого во временной области показана на рис. 2. Значение показателя равномерности синтезированного сигнала составило 83 %. Это указывает на более высокую скрытность синтезированного сигнала по сравнению с сигналами, указанными в таблице, и принципиально более высокую скрытность по сравнению с более низкочастотными сигналами. Направлением дальнейших исследований является научное обоснование выбора параметров сверхширокополосных сигналов для применения в различных системах радиосвязи с учётом их технической реализуемости.
Проведённое моделирование показало эффективность разработанной математической модели для анализа спектров сверхширокополосных сигналов и исследования скрытности систем радиосвязи. Кроме того, разработанная математическая модель показателя равномерности радиочастотного спектра сверхширокополосного сигнала может использоваться в специальном программном обеспечении анализаторов спектра для количественной оценки степени соответствия спектра сигналов радиосистемы выделенному для неё ресурсу радиочастотного спектра.