Беспилотный летательный аппарат – одно из важных достижений в развитии науки и техники. Он может быть запрограммирован на автоматический полет по заранее определенным маршрутам, и им можно управлять удаленно в режиме реального времени. Использование беспилотных летательных аппаратов растет во всех сферах [1, 2]. Существует множество способов управления мобильными роботами, а также беспилотным летательным аппаратом, но SLAM – один из самых интересных. SLAM занимается отображением неизвестной среды с помощью мобильного робота во время навигации по среде с использованием картирования [3, 4]. В последнее время было проведено множество исследований для определения вычислительной эффективности SLAM и объединения данных, а также и для определения всего необходимого для мощного метода SLAM. Целью исследования является разработка и исследование реконфигурируемых алгоритмов и моделей компьютерной среды для обработки информации, создание карт для БПЛА во время его передвижения, что помогает повысить эффективность компьютерной обработки и синтеза данных.
1. Создание алгоритма автоматического отображения для перестраиваемой вычислительной среды (ПВС)
Картирование окружающей среды включает создание математической модели пространственной информации реальной окружающей среды. SLAM расширяет требования этой математической модели, показывая то же состояние робота и положение извлеченных ориентиров относительно его положения [3, 4].
В статье будет показано построение вычислительной среды, настраивающейся в соответствии с предопределенными алгоритмами. Автоматическое реконфигурационное устройство называется автоматом, мощность которого зависит от значения входного сигнала. В настройке этого аппарата используются только базовые входные сигналы 0 и 1. Следовательно, на основе булевых формул можно использовать простые логические вычисления И, ИЛИ, НЕ для настройки реконфигурируемых логических схем [5, 6]. Это автоматическое устройство работает в строго определенное время таким образом, что имеет только одно состояние за раз [7–9].
Для корректировки состава расчет будет основываться на управляющем сигнале разряда z. Это означает, что вычислительный компонент будет состоять из входов x, управляющего сигнала разрядки z и выводов выходного сигнала f. Значения внутреннего и выходного сигналов каждый раз могут быть установлены в соответствии с функциями входного и внутреннего сигналов. Чтобы гарантировать, что логические формулы определены только в классе, для каждой из этих логических формул создаются автоматические сопоставления. Эти булевы формулы построены следующим образом (рис. 1) [10–12]:
1) При z1 = z2 = z3 = z4 = z5 = 0 (рис. 1, а)
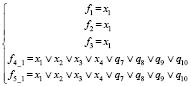
2) При z1 = z2 = z3 = z4 = 0, z5 = 1 (рис. 1, б)
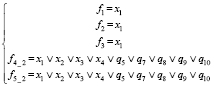
3) При z1 = z2 = z3 = 0, z4 = 1, z5 = 0 (рис. 1, в)
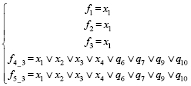
4) При z1 = z2 = z3 = 0, z4 = 1, z5 = 1 (рис. 1, г)
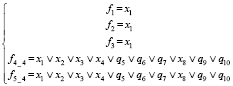
5) При z1 = z2 = 0, z3 = 1, z4 = z5 = 0 (рис. 1, д)
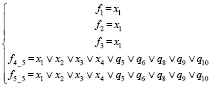
6) При z1 = z2 = 0, z3 = 1, z4 = 0, z5 = 1 (рис. 1, е)
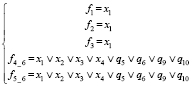
7) При z1 = z2 = 0, z3 = z4 = 1, z5 = 0 (рис. 1, ё)
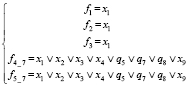
8) При z1 = z2 = 0, z3 = z4 = z5 = 1 (рис. 1, ж)
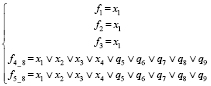
9) При z1 = 0, z2 = 1, z3 = z4 = z5 = 0 (рис. 1, з)
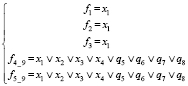
10) При z1 = 0, z2 = 1, z3 = z4 = 0, z5 = 1 (рис. 1, и)
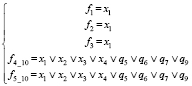
11) При z1 = 0, z2 = 1, z3 = 0, z4 = 1, z5 = 0 (рис. 1, й)
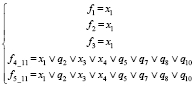
12) При z1 = 0, z2 = 1, z3 = 0, z4 = 1, z5 = 1 (рис. 1, к)
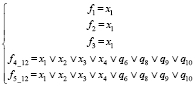
13) При z1 = 0, z2 = 1, z3 = 1, z4 = z5 = 0 (рис. 1, л)
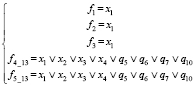
14) При z1 = 0, z2 = z3 = 1, z4 = 0, z5 = 1 (рис. 1, м)
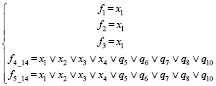
15) При z1 = 0, z2 = z3 = z4 = 1, z5 = 0 (рис. 1, н)
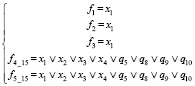
16) При z1 = 0, z2 = z3 = z4 = z5 = 1 (рис. 1, п)
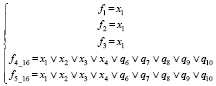
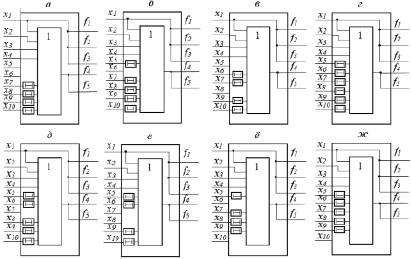
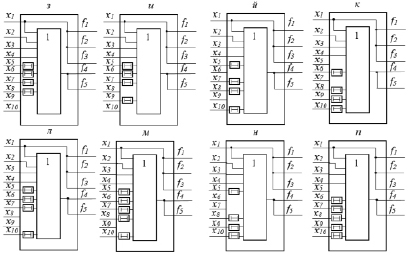
Рис. 1. Модель автоматического картирования
Здесь нам представлен построенный алгоритм элементарных вычислений для 16 блоков ЭВ (элементарных вычислений), каждое из которых соответствует случаю корректировки значений управляющего сигнала при разряде z. Оттуда соединение этих блоков вместе также строится по общей формуле
f1 = x1,
f2 = x1,
f3 = x1,
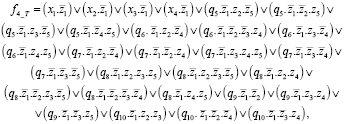 (*)
(*)
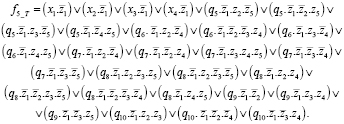
Общая формула выше – это формула для настраиваемой вычислительной среды. Для каждого набора переменной z и входного сигнала эта модель будет получать выходной сигнал, соответствующий 1 из 16 ЭВ, указанных выше. Для каждого набора формул построение модели автоматического отображения будет соответствовать приведенным выше 16 моделям вычислительных компонентов. Например, набор формул 1 будет соответствовать модели 1 (а), набор формул 2 соответствует модели 1 (б)… набор формул номер 16 соответствует модели 1 (п). Наборы этих формул с 1 по 16 определяют набор формул, генерируемых автоматами, и алгоритм настройки для каждого из них. Регулируя значение сигнала на его входной части, можем использовать некоторые преобразователи, чтобы автоматически преобразовывать значения выходного сигнала, поступающего с другого входа, в выходной сигнал [1, 13].
Такая настраиваемая модель вычислительной среды создается в программном обеспечении Matlab, как показано на рис. 2 ниже, включая 10 входов x1, x2, x3, x4, x5, x6, x7, x8, x9, x10, 5 управляющих сигналов разряда z1, z2, z3, z4, z5 и 5 выходов f1, f2, f3, f4, f5.
В зависимости от смоделированной спроектированной среды, элементарные вычисления генерируются для соответствия этой среде.
Эти модели структур Tr-struct действуют как ячейки во всем облаке точек (пространстве, в котором движется робот). В этом исследовании метод Octomap использовался в комбинации. Один из самых эффективных методов создания гибких, постоянно обновляющихся и компактных карт. Начните группировать 4 модели клеток в группу. Когда элемент конструкции изменяется, группа меняет сигнал одновременно с ним. Предполагая, что первый элемент в группе получает значение входного сигнала 1, тогда выходной сигнал первого элемента также будет равен 1, и выход остальных трех элементов также получит сигнал 1. Если элемент в группе принимает значение входного сигнала 0, выходной сигнал участников группы будет нулевым. Таким образом, отображение для робота будет более точным, быстрым и эффективным. Кроме того, этот подход обеспечивает производительность за счет моделирования последовательных данных при минимизации требований к памяти. Кроме того, метод Octomap обеспечивает максимальную гибкость с точки зрения площади и разрешения карты. Потому что этот метод выполняет оценку вероятности для обеспечения возможности обновления и работы с датчиками шума. Octomap обеспечивает эффективный экран сетки в 3D с октодеревьями. Эта модель представлена на рис. 3 [14–16].
2. Новый метод SLAM и имитационного моделирования
Во-первых, создается совершенно произвольная среда для перемещения робота в имитируемой модели Gazebo. Установленный робот Hector-Quadrotor перемещается в среде с препятствиями, спроектированными, как показано на рис. 4 [14].
Когда робот перемещается через систему координат, он будет отслеживать свое положение (получать параметры положения робота) и получать параметры расстояния робота от препятствия через лазерный датчик. Здесь метод SLAM построен следующим образом: предполагается, что размер робота равен размеру ячейки. Вышеупомянутая проектируемая среда имеет размер 12x12 ячеек. Обозначим размер робота как «sr»; ячейку, содержащую препятствие – «CC». По мере движения робота в каждой системе координат отображается его положение, а лазерный датчик указывает расстояние от робота до препятствия. Если расстояние больше, чем k * sr, тогда расстояние между роботом и ячейкой «CC» также будет k * sr (k – действительное число больше 0). Оттуда определяем ячейку, содержащую препятствие. Размерность (или Значение) этих ячеек установлена в 1, у ячеек без препятствий она устанавливается в ноль. Таким образом, при установке на Matlab результат, показанный на рис. 5, является правильной картой для робота, когда он движется в неизвестной среде.
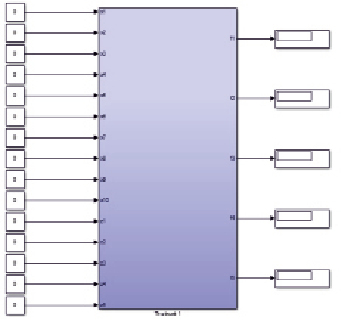
Рис. 2. Модель элементарных вычислений после проектирования

Рис. 3. Модель перестраиваемой вычислительной среды
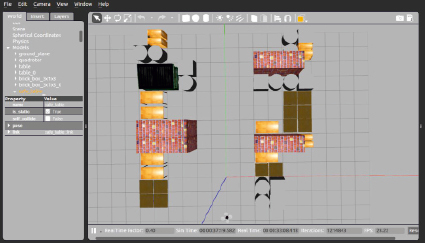
Рис. 4. Искусственная среда для квадрокоптера Hector-Quadrotor

Рис. 5. Карта робота получается перемещением на последнюю позицию
Метод группировки ячеек, описанный выше, реализован в соответствии с методом Octomap для минимизации памяти для элементарных вычислений в реконфигурируемой вычислительной среде, размещаемой на роботе по мере его движения. Благодаря универсальности и компактности робототехнических систем включение Octomap для развертывания карт позволит роботу быстро определять области с препятствиями.
Полученную карту можно визуализировать, как показано на рис. 6.
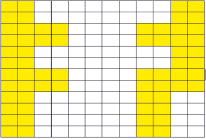
Рис. 6. Карта движения дрона Hector-Quadrotor в среде Gazebo
Создание нового алгоритма для проектирования реконфигурируемой вычислительной среды – это новый подход к SLAM. С помощью этого метода робот может легко получать карту и постоянно обновлять ее, перемещаясь в неизвестном пространстве или в окружающей среде. Таким образом была создана новая вычислительная парадигма, способствующая эволюции сегодняшнего SLAM.
Заключение
Создание нового алгоритма и модели ПВС для картирования UAV является результатом, который данная статья хочет продемонстрировать. Использование адаптируемой модели ПВС на самоходных роботах для картирования ими окружения внесло значительный вклад в разработку новой методологии SLAM. Эта методология улучшает скорость обработки, а также производительность вычислений.



