Начиная с 1960-х гг. широкое промышленное применение различных машин ударного действия [1–4] привело к необходимости разработки методов аналитического описания динамических процессов [5–7], возникающих в них. В настоящее время активное использование ЭВМ позволяет автоматизировать эти расчеты. В связи с этим возникают новые алгоритмы решения динамических задач, которые достаточно легко описываются математическим аппаратом алгоритмических языков программирования (например, Pascal, C++ и т.д.). Составленные на этих языках программы являются кроссплатформенными, что определяет их независимость от коммерческого программного обеспечения. Это делает их конкурентоспособными на современном рынке прикладного программного обеспечения.
Описание продольного удара, применяемого в машинах ударного действия
Продольный удар – это физическое воздействие одного тела на другое, при котором бьющий и принимающий удар объекты до и после взаимодействия движутся вдоль одной прямой. Бьющим называют тело вращения (стержень) переменного сечения, в дальнейшем именуемое бойком, или ударником (рис. 1). Принимающим телом является цилиндр (стержень) постоянного сечения, именуемый в дальнейшем волновод, он заканчивается инструментом (коронкой), который внедряется в разрушаемый объект. Основной динамической характеристикой ударной системы является ее энергоемкость, которая зависит от амплитуды генерируемого силового импульса и его длительности.
Цели исследования: создание численного (аналитического) метода расчета ударного импульса, генерируемого при продольном ударе в стержневых системах переменного сечения, используемых в машинах ударного действия, и разработка комплекса программ, рассчитывающих ударные импульсы от бойков переменного сечения сложной формы.
Материалы и методы исследования
Ударники, применяемые в механизмах, представляют собой сложные тела вращения, определяемые образующей, которая сформирована из нескольких простых кривых, заданных k-функциями вида yk = f(x) (рис. 2А), имеющих области определения L1, L2,..,Lk соответственно. Количество таких кривых может быть любым, оно определяет число ступеней ударника.
Аналитический метод расчета ударного импульса базируется на теории Сен-Венана, где решается задача формирования импульса силы на границе изменения поперечного сечения двух соударяющихся тел [8–10].
Решая подобную задачу, мы предлагаем представить ударник в виде n-го количества цилиндрических ступеней одинаковой длины l1, диаметр которых меняется скачкообразно согласно значениям функций уk = f(x). В итоге получается, что боек превращается в «брикет» (расчетный ударник), состоящий из жестко связанных стержней идеальной формы, который движется со скоростью V0 и наносит удар по полубесконечному неподвижному волноводу, имеющему диаметр d0 (рис. 2Б).
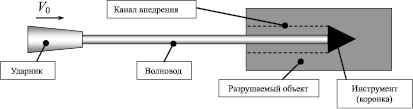
Рис. 1. Схема стержневой ударной системы
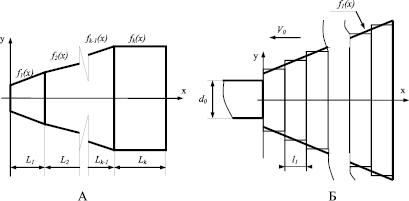
Рис. 2. (А) Формирование сложного ударника. (Б) Представление ударника в виде цилиндрических ступеней конечной длины (на примере первой функции f1(x), составляющей образующую бойка)
При нанесении удара по волноводу в нем возникают силы, величины которых изменяются со временем. Величины этих сил рассчитываются по численным значениям площадей расчетных ступеней, на которые разбит ударник, и сложением прямых и обратных продольных волн деформации, возникших при нанесении удара и распространяющихся со скоростью звука. Ранее для расчета величин этих сил использовался графоаналитический метод [11]. Его анализ показал, что этот метод можно трансформировать в численный и реализовать его на языке программирования (блок-схема этого метода представлена на рис. 3) [12]. Структурно этот расчет можно разбить на шесть операционных этапов.
Этап № 1. Формирование массива, содержащего численные значения площадей цилиндрических ступеней, на которые разбит ударник: Si, где i – номер ступени (всего n ступеней), S0 – площадь поперечного сечения волновода (в рамках решаемой задачи постоянная величина).
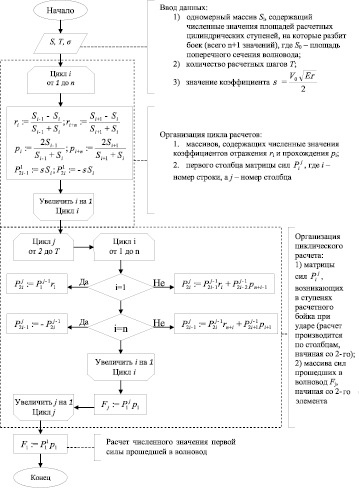
Рис. 3. Блок-схема численного метода расчета сил, прошедших в волновод при продольном ударе, нанесенном ударником переменного сечения
Определение физических параметров системы: E – модуль упругости и ρ – плотность материала бойка и волновода (в рамках решаемой задачи материалы одинаковые), V0 – предударная скорость бойка.
Определение расчетных параметров системы: a – скорость звука в материале бойка и волновода; T – количество расчетных шагов (равных временных отрезков, на которые разбит весь процесс одного удара).
Этап № 2. Расчет коэффициентов прохождения pi и отражения ri продольной волны смещений в ступенях ударника.
Этап № 3. Расчет элементов матрицы сил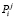 
, возникающих в ступенях бойка при соударении с течением времени.
Этап № 4. Формирование массива сил, прошедших через границу соударения бойка и волновода.
Этап № 5. Расчет времени действия каждой силы t1 и времени длительности t всего импульса.
Этап № 6. Построение графика ударного импульса, представляющего собой гистограмму сил, прошедших в волновод за все расчетное время t (рис. 4).
Результаты исследования и их обсуждение
На базе разработанного численного метода создан комплекс расчетных программ, которые отличаются друг от друга способами моделирования расчетных ударников. Все программы этого комплекса имеют схожую структуру и написаны на языке программирования PASCAL в среде LАZARUS.
Методы формирования ступенчатых (расчетных) ударников
I. Моделирование одноступенчатого ударника по известной массе и длине расчетной цилиндрической ступени. Программа «Ударный импульс 2.0» [13].
Под одноступенчатым ударником следует понимать реальное цилиндрическое тело переменного сечения, образующая которого сформирована из одной простой кривой, заданной функцией f(x).
Данный метод предполагает не разбивать какой-то существующий ударник на расчетные ступени, а сформировать его из них путем добавления к имеющейся ступени новой, отличающейся по диаметру. Формирование ступеней следует проводить до тех пор, пока суммарная масса всех набранных элементов не станет равна заданной массе в пределах допустимой погрешности (≈ 4–5 %):
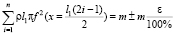, (1)
где i – номер текущей цилиндрической ступени; n – количество цилиндрических ступеней; ρ – плотность материала бойка и волновода; l1 – длина цилиндрической ступени (задается произвольно и является параметром, определяющим число n и величину итоговой погрешности в каждом расчете);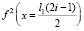 
– квадрат значения функции образующей от аргумента, равного координате середины текущей цилиндрической ступени; m – заданная масса ударника; ε – величина относительной погрешности.
Для реализации этого метода подошел алгоритм с предусловием (рис. 5). Его отличием от математической модели (1) является то, что погрешность не задается, а рассчитывается после формирования расчетного ударника, так как ее значение необходимо для оценки смоделированного в данном конкретном случае бойка (а конкретно – выбора длины расчетной ступени).
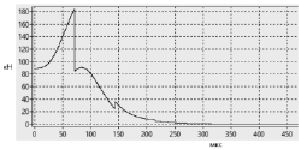
Рис. 4. График ударного импульса, представленный в виде гистограммы сил, прошедших в волновод, численные значения которых получены в ходе расчета по алгоритму численного метода
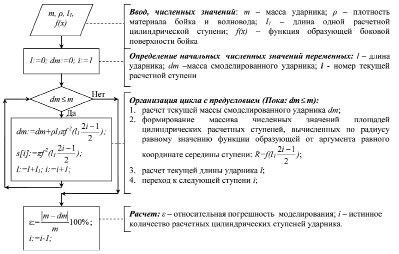
Рис. 5. Блок-схема алгоритма моделирования одноступенчатого ударника (образующая задана одной функцией f(x)) по известной массе и длине расчетной цилиндрической ступени
Рис. 6. Блок-схема моделирования многоступенчатого ударника по известным геометрическим параметрам и массе бойка
Данный метод предполагает разбиение уже существующего ударника на цилиндрические расчетные ступени одинаковой длины l1. Расчет величины диаметра текущей расчетной цилиндрической ступени следует производить по значению функции y = fk(x), определяющей текущую кривую в сложной образующей ударника:
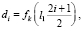(2)
где i – номер текущей расчетной цилиндрической ступени, а l1 – ее длина. Выбор функции происходит путем проверки принадлежности значения аргумента функции в выражении (2) к области определения соответствующей функции:
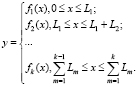(3)
II. Блок-схема моделирования многоступенчатого бойка [14] предложена на рис. 6. Следует отметить, что геометрические параметры (Li – длина ступеней ударника и l1 – длина расчетной цилиндрической ступени) могут быть определены по алгоритму моделирования одноступенчатого ударника (рис. 5) путем формирования каждой ступени индивидуально.
III. Моделирование ударника в стороннем приложении. Программа «Анализ ударного импульса» [15].
Рис. 7. 3D-модель бойка от погружного пневмоударника, выполненная в программе T-Flex
Большинство реальных ударников, применяемых на практике, не поддаются численному моделированию способами, описанными выше, но предложенный численный метод работает и для таких тел. Для этого ударник моделируется в стороннем приложении (например, КомпАс, T-Flex и т.п.). Строится 3D-модель такого ударника (рис. 7) с использованием ресурсов приложения, далее она делится на цилиндрические ступени одинаковой длины l1 с сопутствующим расчетом площади поперечного сечения каждой ступени. Численные значения этих площадей записываются в текстовый файл, который является входным параметром для формирования расчетного ударника цельнотельной формы (рис. 7).
Заключение
В ходе работы создан универсальный численный метод расчета сил, прошедших в волновод при нанесении удара цилиндрическим телом переменного сечения. На базе этого метода написан комплекс расчетных программ, позволяющих аналитически рассчитывать ударные импульсы от бойков различной формы (от простых до самых сложных). Также разработаны методы численного моделирования цельнотельных цилиндрических ударников переменного сечения, которые успешно реализованы на практике.