В общем случае оптимизацию трассы в плане предлагается осуществлять в два этапа. Оба этапа выполняются по критерию суммарных приведенных затрат в определенной зоне варьирования на основе информационной модели, имеющей необходимые для поиска трассы данные о технико-экономических характеристиках проектируемой лесовозной автомобильной дороги и полосы варьирования.
Цель работы заключается в исследовании методов проектирования трасс лесовозных автомобильных дорог с применением геоинформационных технологий, отличающихся постановкой задачи, способами их решения, характером геометрического представления трассы и другими особенностями.
Материалы и методы исследования
На первом этапе информационная модель строится на основе эскизной линии, которая либо задается инженером, либо может быть получена автоматически программным путем, как это рекомендовано в работах [1–3]. Эскизная линия отражает лишь грубый выбор во множестве возможных вариантов трассы, поиск наилучшего из которых осуществляется по принятому критерию с использованием предложенного метода оптимизации. Решение отыскивается в виде состоящей из отрезков прямых линий, приближенно отвечающей требованиям, предъявляемым к геометрическим параметрам оси дороги (по кривизне, изменению кривизны и др.). В дальнейшем будем именовать данную постановку задачи оптимизацией «цепочечной» трассы.
В качестве переменных в этом случае приняты Zi – отклонения оптимизируемой трассы от заданной приближенной.
1. Выполнение условий отмыкания и примыкания трассы, прохождения ее через заданные контрольные точки, а также фиксация границ зоны варьирования обеспечиваются ограничениями вида:
Zmini ≤ Zi ≤ Zmaxi, i = 1, 2, …, I, (1)
где Zmini и Zmaxi – минимально и максимально допустимое значение Zi.
2. Для точек 2,… I-1 выполняется проверка требования
Кmini ≤ Кi ≤ Кmaxi, (2)
где Кi – кривизна в точке Qi оптимизируемой трассы, определяемая как кривизна окружности, проходящей через точки Qi-1, Qi и Qi+1;
Кmini, Кmaxi – минимально и максимально допустимая кривизна.
Строгая формализация данного требования сложна и Кi = f(Zi) в общем случае не линейна относительно Zi.
Рассмотрена возможность линеаризации Кi = f(Zi) с использованием усеченного ряда Тейлора:
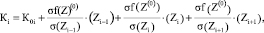 (3)
(3)
где К0i – кривизна эскизной линии в i-й точке.
Аппроксимируя частные производные разностными соотношениями, получим
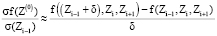 , (4)
, (4)
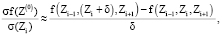 (5)
(5)
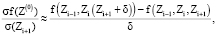 (6)
(6)
где δ – некоторые малые отклонения переменных.
В целях увеличения точности аппроксимирующей зависимости (3) в нее вводится поправка на удаление расчетной трассы от эскизной линии при одновременном изменении Zi-1, Zi и Zi+1.
С учетом этой поправки зависимость f(Z) принимает следующий вид:
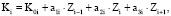 (7)
(7)
где
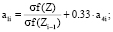
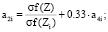
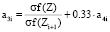 ;
;
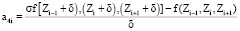 .
.
3. Для точек 3,…,1–2 должно обеспечиваться выполнение требования
Аmini ≤ Аi ≤ Аmaxi, (8)
где Аmini, Аmaxi – минимально и максимально допустимый параметр клотоиды. Минимальные параметры переходных кривых устанавливаются из условия обеспечения нормируемой величины изменения центробежного ускорения У, (как правило, для дорог общего пользования |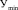 | = 0.5 м/с3). В общем случае
| = 0.5 м/с3). В общем случае
Уmini ≤ Уi ≤ Уmaxi, (9)
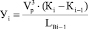 , (10)
, (10)
где Vp – расчетная скорость движения лесовозного автопоезда;
Кi, Кi-1 – кривизна, соответственно в точках i и i-1,
LBi-1 – расстояние между точками QNi и QN(i-1) эскизной трассы.
Из формулы (10) видно, что ограничения (9) будут иметь линейный характер относительно переменных Zi только в том случае, если Кi = f(Zi) линейная функция. Линеаризация Кi может быть выполнена по формулам (7).
Анализ показывает, что погрешности за счет линеаризации ограничений (2) и (9) зависят в основном от величин Zmini, Zmaxi, Kmini, Kmaxi и можно выбрать такую ширину зоны варьирования, которая бы обеспечила требуемую точность.
Таким образом, удается представить все ограничения в виде системы линейных неравенств:
ВZ ≤ D;
где В – блочная матрица вида:
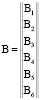 ;
;
В1 – диагональная матрица размерностью (1х1) ограничений вида –Zi ≤ –Zmini;
В2 – диагональная матрица (1х1) ограничений вида Zi ≤ Zmaxi;
В3 – матрицы (1х1-2) ограничений вида –Кi ≤ –Кmini;
В4 – матрицы (1х1-2) ограничений вида Кi ≤ Кmaxi;
В5 – матрицы (1х1-2) ограничений вида –Уi ≤ –Уmini;
В6 – матрицы (1х1-2) ограничений вида Уi ≤ Уmaxi.
Так как К1 является выпуклой квадратичной функцией 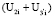 = f(Zi) с достаточной точностью аппроксимируется выпуклыми кусочно-квадратичными зависимостями, то Рпр, согласно работе [4], также является выпуклой функцией.
= f(Zi) с достаточной точностью аппроксимируется выпуклыми кусочно-квадратичными зависимостями, то Рпр, согласно работе [4], также является выпуклой функцией.
Таким образом, проектирование оптимальной «цепочечной» трассы приводится к задаче выпуклого математического программирования с линейными ограничениями в виде неравенств. Она формулируется следующим образом:
минимизировать Рпр = f(Z), Z∈ En, (11)
при линейных ограничениях в виде неравенств ВZ ≤ D.
Решение может быть выполнено с применением методов нелинейного программирования.
На втором этапе оптимизации информационная модель строится на основе базового варианта трассы, представленного в виде клотоид, отрезков клотоид, круговых кривых и прямых, соответствующим образом сопряженных. Последовательность элементов трассы в процессе оптимизации сохраняется, но происходит изменение геометрических характеристик, которые принимаются в качестве переменных, и, как следствие этого, меняется положение проектируемой оси лесовозной автомобильной дороги. В дальнейшем данную постановку задачи будем именовать оптимизация геометрических характеристик элементов трассы [5, 6].
Данная задача формулируется следующим образом.
Используя в качестве начального приближения геометрические характеристики базовой трассы и основываясь на данных с технико-экономических показателях полосы варьирования, найти положение и геометрические характеристики трассы, состоящей из клотоид, круговых кривых и прямых, которая:
- удовлетворяет требованиям;
- имеет минимум суммарных приведенных затрат.
Рассмотрим два возможных способа линеаризации:
1) с приближенным определением ΔτQ, ΔlQ, ΔLQ;
2) с использованием усеченного ряда Тейлора в окрестности Х(k).
1. В случае использования значения (ΔτQ, ΔlQ, ΔLQ) могут быть определены по приближенным зависимостям (рис. 1).
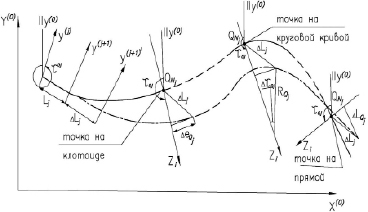
Рис. 1. Схема формирования линеаризованных зависимостей
Например, когда переменной характеристикой является длина прямой ΔLm, то для точки Qi, находящейся на прямой:
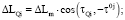
на круговой кривой:
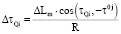 ;
;
на клотоиде:
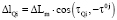 .
.
В общем виде для случая переменной длины прямой:
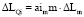 ;
;
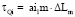 ;
;
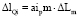 ,
,
где а – коэффициент пропорциональности.
Первый индекс при а указывает, на каком элементе i-я точка: im – на прямой, il – на круговой кривой, ip – на клотоиде. Второй индекс указывает вид переменной: m – длина прямой, l – центральный угол круговой кривой, n – радиус круговой кривой, p – параметр клотоиды.
Аналогичным образом (ΔτQ, ΔlQ и ΔLQ определяются в случаях, когда переменными характеристиками являются 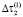 – центральный угол круговой кривой:
– центральный угол круговой кривой:
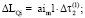
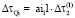 ;
;
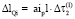 ;
;
ΔRn – радиус круговой кривой:
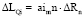 ;
;
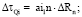
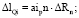
ΔAp – параметр круговой кривой:
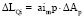 ;
;
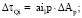
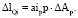
Затем определяются элементы матрицы С с учетом того, что 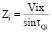 , где τQi – угол между осями У(0) и Zi (рис. 2).
, где τQi – угол между осями У(0) и Zi (рис. 2).
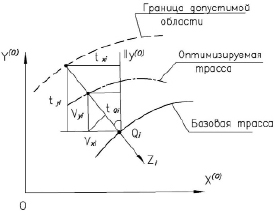
Рис. 2. К определению элементов матрицы С
2. Для определения элементов матрицы С с использованием усеченного ряда Тейлора для функции многих переменных имеем
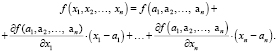
В точке с координатами
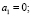
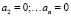
имеем f(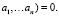
Тогда:
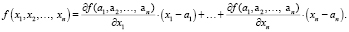
Значения частных производных могут быть вычислены по аналогии.
Из приведенных исследований видно, что проектирование оптимальной трассы в плане при фиксированном продольном профиле может быть представлено как задача выпуклого математического программирования:
минимизировать:
f(X), Х∈ En,
при линейных ограничениях в виде неравенств:
ВХ ≤ D.
Описание методов решения задач данного вида приведено в работах [7–10].
Так же как и в случае с переменными Z, необходимо выполнить несколько итераций с последовательным уточнением модели 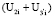 = f(Zi) и линеаризованных зависимостей Zi = f(X).
= f(Zi) и линеаризованных зависимостей Zi = f(X).
Заключение
Методы нелинейного математического программирования, используемые для решения задачи оптимизации трассы в плане при фиксированном продольном профиле, позволяют находить локальный минимум. В случае унимодальной целевой функции локальный и глобальный минимумы совпадают. Поэтому предлагаемые методы целесообразно использовать на завершающем этапе проектирования и для уточнения положения трассы в относительно узкой зоне варьирования, для которой могут быть построены достаточно точные модели критерия, обеспечивающие унимодальности целевой функции.



