Принятие решений на всех стадиях жизненного цикла различных объектов всегда осуществляется при наличии неуверенности в том, что их выполнение приведет к достижению желаемой цели, а также опасения того, что это может привести к тяжелым последствиям. Свойство решения, характеризующее возможность и последствия недостижения его целей, будем называть свойством рискованности или, кратко, риском [1]. Для количественного анализа характеристик этого свойства широко используются математические модели, отражающие вероятностную природу неопределенностей, при наличии которых принимаются решения. Однако результаты их использования будут справедливы только тогда, когда у нас есть уверенность в точном знании как самих моделей, так и значений их параметров. В действительности полной уверенности в справедливости сделанных предположений и истинности численных значений используемых параметров никогда не бывает. Поэтому возникает необходимость в применении математических средств, которые бы позволили учесть неопределенность знаний, по крайней мере, о значениях параметров, применяемых вероятностных моделей. Неопределенность, обусловленная отсутствием достаточных знаний, называется эпистемической неопределенностью. Название происходит от лат. episteme – знание.
Существует несколько подходов к изучению эпистемической неопределенности с использованием количественных оценок. Прежде всего, следует назвать подходы, основанные на применении методов теории интервального анализа [2], теории доказательств Демпстера – Шефера [3] и концепции вероятностей второго порядка. Названные теории характеризуются высоким уровнем сложности и их систематическое применение для решения прикладных задач связано с необходимостью использования больших ресурсов. Поэтому актуальной является задача снижения уровня сложности применяемой технологии исследования системы, без ухудшения ее качества [4].
В настоящей статье рассматривается возможность использования байесовского подхода к учету неопределенности знаний параметров вероятностных моделей, используемых при обосновании решений, принимаемых на стадии эксплуатации технических устройств (ТУ).
Общая схема применения байесовского подхода
Правила преобразования априорных знаний о некотором параметре θ, в истинности значения которого есть сомнения, на основании полученных дополнитеольных данных x определяются формулой Байеса [5]:
π(θ|x) =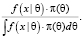 
(1)
В этой формуле: f(x|θ) – условная плотность распределения наблюдаемого параметра x, если он изменяется непрерывно, или распределение Бернулли, если он изменяется дискретно; π(θ) – априорная плотность распределения параметра θ, которая характеризует априорные знания о параметре θ; интеграл в знаменателе берется по всему диапазону параметра θ; π(θ|x) – апостериорное распределение ненаблюдаемого параметра θ после получения дополнительной наблюдаемой информации x; интеграл в знаменателе вычисляется по интервалу изменения параметра θ.
На рис. 1 представлена обобщенная схема применения байесовского подхода к учету неопределенности параметров вероятностных моделей.
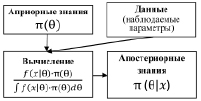
Рис. 1. Обобщенная схема применения байесовского подхода
В общем случае определение апостериорной плотности распределения вероятностей случайных событий, например, отказов, в истинности значений которых нет уверенности, является сложным вычислительным процессом из-за необходимости вычисления интеграла в знаменателе формулы Байеса. Этот процесс существенно упрощается, если вычисления производить не с исходными априорными плотностями распределения, а с их сопряженными распределениями [5]. Распределение π(θ) называется сопряженным априорным распределением к семейству функций правдоподобия f(x|θ), если ее апостериорное распределение π(θ|x) принадлежит тому же семейству вероятностных распределений, что и априорное распределение π(θ) (т.е. имеет тот же вид, но с другими параметрами) [6].
Рассмотрим, как в процессе эксплуатации ТУ, используя байесовский подход, можно корректировать значения параметров математических моделей отказов, необходимых для анализа риска принимаемых решений, и сделаем это на примере двух законов распределения: биномиального и экспоненциального.
Коррекция параметра биномиального закона распределения
Биномиальное распределение имеет место, если выполняются следующие условия: существует два возможных результата выполнения требования, обычно интерпретируемых как успех и неудача; существует постоянная вероятность отказа в выполнении каждого требования; результаты более ранних требований не влияют на результаты более поздних требований (т.е. порядок неудач/успехов не имеет значения).
Будем полагать, что такие условия выполняются в процессе функционирования системы управления состоянием предохранительного клапана, предназначенного для снятия избыточного давления в ТУ. При выдаче контроллером команды (требования) на открытие клапана возможны два исхода: срабатывание клапана и сброс давления в ТУ и отказ в выполнении требования (отказ клапана).
Количество отказов m в выполнении n требований характеризуется распределением Бернулли
p(m|n, q) =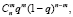 
(2)
где q – вероятность невыполнения требования; n – количество требований, имевших место; m – количество наблюдаемых отказов в выполнении требований;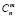 
– число сочетаний из n по m; p(m|n, q) – вероятность невыполнения ровно m требований из n при вероятности невыполнения каждого требования q (функция правдоподобия).
Корректируемый параметр в этой модели, в истинности количественного значения которого есть сомнения, в данном случае – q, а наблюдаемые данные – количество требований n и количество отказов m в их выполнении. Предполагается, что m и n достоверно известны.
В данном случае имеет место следующее сопоставление принятых здесь обозначений с обозначениями в формуле Байеса (1):
q = θ, x = m, p (m|n, q) = f(x|θ),
π(q) = π(θ), π(q|m) = π(θ|x).
Сопряженным функции правдоподобия p(m|n, q) априорным распределением π(q) является бета-распределение, которое в принятых обозначениях имеет вид
π(q) =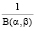 
qα-1(1 – q)β – 1, (3)
где B(α, β) =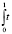 
α-1(1 – t)β-1 dt – бета-функция [5].
Подставив (2) и (3) в формулу Байеса (1) и произведя несложные преобразования, получим выражение для апостериорного распределения не наблюдаемого параметра q после получения дополнительной наблюдаемой информации m
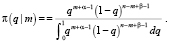
Нетрудно заметить, что интеграл в знаменателе этого выражения равен бета-функции B(α + m – 1, β + n – m – 1) и, следовательно, апостериорное распределение, так же как и априорное, представляет собой бета-распределение, но с другими параметрами и имеет вид
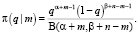(4)
В данном случае параметр альфа-априорного распределения αапр концептуально можно рассматривать как количество невыполненных требований, а сумму (αапр + βапр) – как общее количество требований [5]. Зная апостериорные данные, состоящие из m отказов в n требованиях, можно определить параметры апостериорного распределения [5]:
αапост = αапр + m, (5)
βапост = βапр + n – m. (6)
Как отмечено выше, для исследования апостериорных и априорных распределений можно использовать встроенные функции электронной таблицы Microsoft Excel. Для получения плотности вероятности бета-распределения случайной величины используется функция БЕТА.РАСП, возвращающая функцию или плотность бета-распределения, а для получения границ байесовского доверительного интервала – функция БЕТА.ОБР, возвращающая обратную функцию бета-распределения.
Рассмотрим простой пример. Дано: априорная плотность распределения π(q) (3) с параметрами αапр = 2; βапр = 1000; апостериорные данные: количество требований n = 500, количество невыполненных требований m = 2.
Найти: параметры апостериорной плотности распределения π(q|m); средние значения вероятности того, что требование не будет выполнено при использовании априорной π(q) и апостериорной π(q|m) плотностей вероятности q; 90 % байесовские доверительные интервалы для q, используя априорную и апостериорную плотности ее распределения.
Решение. Параметры апостериорной плотности распределения π(q|m) αапост и βапост определяем по формулам (5) и (6) соответственно: αапост = 2 + 2 = 4 и βапост = 1000 + + 500 – 2 = 1498.
Так как параметр q изменяется в пределах от 0 до 1, то его априорное и апостериорное средние значения могут быть определены по формулам
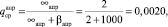
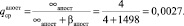
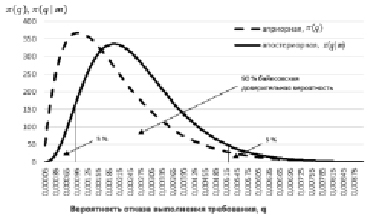
Рис. 2. Сравнение априорной и апостериорной плотностей распределения вероятности параметра q
Для определения границ 90 % доверительного интервала для q воспользуемся функцией электронной таблицы Excel БЕТА.ОБР (…).
Левая граница этого интервала определяется значением q, при котором вероятность отказа в выполнении требования меньше 5 %, а правая – значением q, при котором в 95 % случаев имеет место отказ в выполнении требования. Формат обращения к программам вычисления левой и правой границ байесовского доверительного интервала имеет вид БЕТА.ОБР (0,05, α, β) и БЕТА.ОБР (0,95, α, β). Для αапост = 4 и βапост = 1498 получаем, что интересующий нас параметр q (вероятность невыполнения требования) с вероятностью 0,9 находится в интервале [9,11•10-4; 5,16•10-3] (байесовский интервал). Применив такую же процедуру для априорной плотности распределения с параметрами αапр = 2, βапр = 1000, получим, что этот параметр с вероятностью 0,9 находится в интервале [3,55•10-4; 4,73•10-3].
Проведенные расчеты свидетельствуют о том, что учет дополнительных наблюдений позволил уменьшить неопределенность знаний о значении параметра q, что иллюстрируется графиками, представленными на рис. 2.
Коррекция параметра экспоненциального закона распределения
При принятии решений в процессе эксплуатации технических устройств одним из самых распространенных факторов риска являются их отказы. Если эти отказы характеризуются следующими особенностями: вероятность отказа на небольшом временном интервале приблизительно пропорциональна его длине; вероятность одновременных отказов за короткий промежуток времени равна нулю; возникновение отказа в одном временном интервале не влияет на вероятность возникновения в другом, неперекрывающемся интервале времени (отсутствует последействие), то наблюдаемая случайная величина - время до наступления отказа характеризуется экспоненциальным законом распределения с плотностью распределения вероятности, которая имеет вид
f(t) = λ exp(-λt) при t ≥ 0. (7)
Сопряженным экспоненциальному распределению является гамма-распределение [6] с плотностью вероятности
π(λ|α, β) =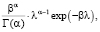 
(8)
где Γ(α) – гамма-функция Эйлера.
Параметры α и β плотности распределения (8) в данном случае имеют следующую интерпретацию [5]: α – количество наблюдаемых интервалов безотказной работы, n; β – суммарная продолжительность интервалов безотказной работы.
Исходя из этой интерпретации, параметры апостериорной плотности вероятности ∞апост и βапост будем определять по формулам
∞апост = ∞апр + n, (9)
βапост = βапр +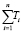 
, (10)
где Ti – продолжительность i-го интервала безотказной работы; ∞апр и βапр – значения параметров априорной плотности распределения.
Из свойств гамма-распределения следует, что среднее значение λ определяется отношением
λср =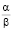 
. (11)
Для определения левой и правой границ γ % доверительного интервала можно воспользоваться встроенной функцией электронной таблицы Excel ГАММА.ОБР (…) с соответствующими форматами обращения:
λлев = ГАММА.ОБР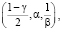 
(12)
λпр = ГАММА.ОБР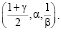 
(13)
Рассмотрим пример.
Дано: результаты фиксации продолжительности работы циркуляционного насоса Ti в часах до 7 отказов (n = 7): 55707, 255092, 58776, 11646, 11358772, 875209, 68978; параметры априорной плотности вероятности ∞апр = 1,6 и βапр = 365000 ч.
Уточнить на основе выполненных наблюдений априорные сведения о параметре λ (интенсивности отказов), определив для него доверительный интервал с доверительной вероятностью γ = 90 % и среднее апостериорное значение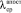 
.
Решение. Определим суммарную продолжительность интервалов безотказной работы насоса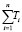 
= 12782180 ч.
Теперь есть вся необходимая информация для определения по формулам (9) и (10) значений параметров α и β апостериорной плотности распределения вероятности:
∞апост = ∞апр + n = 1,6 + 7 = 8,6,
βапост = βапр +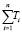 
, = 365000 + 12782180 = 13147180.
Зная эти параметры и используя формат обращения к программе вычисления границ байесовского доверительного интервала (12), определим его левую границу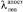 
= 3,4•10-7 ч-1.
Используя формат (13), получим правую границу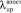 
= 1,1• 10-6 ч-1.
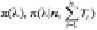
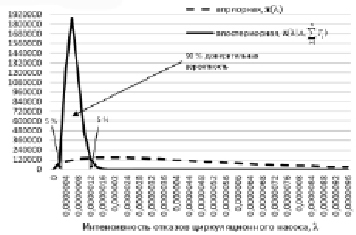
Рис. 3. Сравнение априорной и апостериорной плотностей распределения вероятности параметра λ
Таким образом, можно сделать вывод о том, что учет дополнительной информации об отказах насоса, полученной в процессе его эксплуатации, позволяет утверждать, что с вероятностью 0,9 интенсивность отказов насоса находится в интервале
λапост ∈ [3,4• 10-7 ч-1, 1,1• 10-6 ч-1]. (14).
Аналогичным образом можно определить априорный доверительный интервал
λапр ∈ [5,7• 10-7 ч-1, 1,1• 10-5 ч-1]. (15)
Этот интервал гораздо шире апостериорного интервала.
После получения дополнительной информации о функционировании насоса существенно смещается в сторону меньших значений среднее значение λ, определяемое по формуле (11):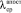 
= 6,7•10-7 ч-1, 
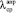= 4,4•10-6 ч-1.
Как и в предыдущем примере, проведенные расчеты свидетельствуют о том, что учет дополнительных наблюдений позволил уменьшить неопределенность знания интенсивности отказов насоса, что иллюстрируется графиками, представленными на рис. 3.
Снижение неопределенности знания параметра λ экспоненциального закона, естественно, приводит к снижению неопределенности знания одного из показателей риска – вероятности отказа циркуляционного насоса в течение заданного времени q(t) = 1 – exp(-λt).
Предположим, что одной из целей создания этого насоса является обеспечение его безотказной работы в течение 100000 ч. Тогда, подставив в эту формулу t = 100000, а затем последовательно значения λ, соответствующие левой и правой границам их апостериорного (14) и априорного (15) 90 % доверительных интервалов, получим аналогичные доверительные интервалы для апостериорной (16) и априорной (17) вероятностей недостижения цели создания насоса:
qапост(100000) ∈ [0,033; 0,104], (16)
qапр(100000) ∈ [0,055; 0,667]. (17)
Сравнение интервалов (16) и (17) показывает, что учет дополнительной информации об отказах насоса на основе применения байесовского подхода позволил получить существенно более точную интервальную оценку показателя риска недостижения цели.
Заключение
Изложенный материал наглядно иллюстрирует, что благодаря возможности использования прикладных программ, содержащихся в электронной таблице Excel, трудоемкость применения байесовского подхода для количественной оценки эпистемической неопределенности параметров законов распределения, применяемых при анализе риска принимаемых решений, и для которых сопряженными являются бета- или гамма-распределения, несравненно меньше, чем трудоемкость применения общих подходов к исследованию неопределенности, базирующимися на теории доказательств Демпстера – Шефера или концепции вероятностей (гистограмм) второго порядка. Это позволяет широко использовать его при анализе риска принятия решений на различных стадиях жизненного цикла продукции, а также в учебной деятельности.