Метод георадиолокации в настоящее время является наиболее передовым и производительным методом при решении задач инженерно-геологических исследований. Основанием метода служит изучение отклика объектов зондируемой среды, различающихся электрическим сопротивлением и диэлектрической проницаемостью, на излучение электромагнитных импульсов. Основная цель георадиолокации состоит в определении состава, физических свойств и структуры геологической среды по полученным данным радиолокационных сигналов. Поэтому весьма актуальными являются задачи исследования алгоритмов, позволяющих достоверно определять положение, размеры и электрофизические свойства объектов: границ раздела сред, локальных неоднородностей и других.
На сегодняшний день существует ряд методик, частично автоматизирующих задачи нахождения полезных сигналов среди всех отраженных сигналов от границ объектов, образованных локальными неоднородностями и различными слоями среды. Набор таких сигналов представлен изображением, называемым радарограммой, а линия, соединяющая максимальные сигналы электромагнитной волны, называется осью синфазности.
Основная трудность при анализе волновой картины радарограмм связана с наличием шума и волн-помех. Поэтому для выделения полезных сигналов, например, дифрагированных волн, представляющих оси синфазности, необходимы этапы предварительной обработки. На аппаратном уровне данная проблема частично решается настройкой зависимости усиления/ослабления амплитуды сигнала радиолокатора от глубины проникновения.
Большинство существующих программных средств, представленных на рынке систем обработки радарограмм, предполагают «ручной» способ подбора формы оси синфазности. Например, в программном обеспечении «GeoScan32» (разработка ООО «Логические системы») пользователю предлагается ручное наложение теоретической гиперболы на видимую ось синфазности до ее полного совмещения (рис. 1). При таком способе обнаружения дифрагированных волн достоверность результатов зависит от человеческого фактора и опыта пользователя-геофизика.
Автоматизация распознавания дифрагированных волн на радарограммах позволит упростить данный процесс и в конечном итоге увеличит точность определения геофизических характеристик подстилающей среды [1].
Цель исследования – создать алгоритм для обнаружения осей синфазности на георадарограммах. Данный алгоритм был реализован в программной разработке, предназначенной для исследования электрофизических свойств грунтов. Приложение было разработано на платформе .NET с использованием объектно-ориентированного языка программирования C#. Для работы с изображениями была использована библиотека AForge.NET – библиотека .NET с открытым исходным кодом, предназначенная для решения задач, связанных с компьютерным зрением. Данная платформа содержит большой набор библиотек, связанных с обработкой изображений, машинным зрением, обработкой видеоданных, вычислениями нейронных сетей, робототехникой и т.д.
Логику работы модуля приложения, содержащего методы по нахождению гиперболических осей синфазности можно описать в виде последовательности шагов:
1. Загрузка изображения радарограммы из файлов .bmp, .jpg, .png, .gif, .tif.
2. Применение фильтров для предварительной обработки (удаление/ослабление шума, изменение яркости, контрастности, резкости, пороговая бинаризация и т.п.).
3. Выделение средней линии значимых областей.
4. Распознавание осей синфазности.
Каждый этап подробно освещается в отдельном пункте статьи.
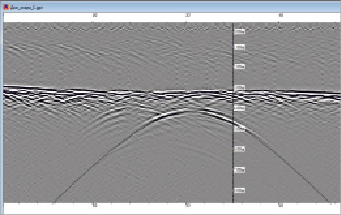
Рис. 1. Наложение теоретической гиперболы на ось синфазности в программе GeoScan32
Фильтры предварительной обработки
Предварительная обработка дискретных изображений имеет большое значение для подготовки их к распознаванию образов. От того, насколько четко и контрастно выделены значимые объекты, зависит успешность этапа распознавания. В разработанном приложении радиолокационные сигналы были рассмотрены в виде двумерной матрицы цифрового изображения, где значения амплитуд были переведены в значения яркости пикселей. Для исследования были выбраны радарограммы, представляющие изображения методом переменной плотности, где увеличение амплитуды сигналов соответствует уменьшению яркости серого цвета. Таким образом, отрицательным значениям амплитуд соответствует белый цвет, а положительным – более темные тона [2]. С этой точки зрения для анализа радарограмм можно успешно применять известные алгоритмы и методы работы с цифровыми изображениями, поскольку значительный перепад яркости и контрастность на георадарограммах говорит о наличии в этих областях границ слоев и осей синфазности.
Усилению полезных сигналов и ослаблению шумов способствуют методы фильтрации. Частотный спектр шума может перекрывать полезные сигналы частично либо перекрывать полезный диапазон сигналов полностью. Поэтому важно подбирать фильтры таким образом, чтобы при снижении шума и ослаблении помех оси синфазности оставались четко отслеживаемыми (рис. 2).
Использование линейных сглаживающих фильтров, например фильтра Гаусса, позволяет успешно снижать уровень шума, размывая изображение, но при этом затрагиваются также границы объектов [3]. В этом случае предпочтительным является применение нелинейных сглаживающих фильтров, например медианного, билатериального, диффузионного. Пример использования шумоподавляющих фильтров для обработки изображений в приложении представлен в таблице.
После снижения уровня шума, при необходимости, можно выполнить настройку уровня яркости/контрастности. Последний этап предобработки – бинаризация – служит целью четкого выделения контрастных областей и удаления фона на изображении. При бинаризации происходит преобразование цвета пикселей в черный при установленном пороге показателя яркости, остальные пиксели окрашиваются в белый цвет (рис. 3).
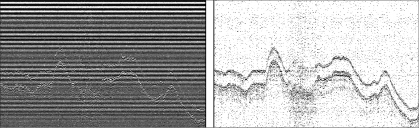
Рис. 2. Удаление горизонтального шума медианным фильтром
Использование сглаживающих фильтров
|
1.1. Исходное изображение |
2.1. Исходное изображение |
|
Окончание таблицы |
|
|
1.2. Билатериальный фильтр, сглаживание s = 10, размер апертуры k = 25, дисперсия цвета c = 200 |
2.2. Билатериальный фильтр, сглаживание s = 200, размер апертуры k = 25, дисперсия цвета c = 10 |
|
1.3. Фильтр анизотропной диффузии Перона – Малика [4], порог размытия t = 10, чувствительность к границам k = 30 |
2.3. Фильтр анизотропной диффузии Перона – Малика [4], порог размытия t = 10, чувствительность к границам k = 10 |

Рис. 3. Пороговая бинаризация
Выделение средней линии значимых областей
Часто полезный диапазон частот образует на радарограммах оси синфазностей, имеющие достаточно неопределенную широкую полосу (рис. 4). Поэтому их программная геометрическая интерпретация не позволяет однозначно подбирать подходящую по форме теоретическую гиперболу.
Для решения данной проблемы в приложении был создан метод, называемый далее «утончением области» (рис. 5). Указанный метод позволяет сужать темные области до средней линии. Данная линия представляет совокупность точек, являющихся серединами отрезков, полученных при пересечении темных областей вертикальными прямыми, последовательно наложенными на изображение.

Рис. 4. Область полезных сигналов
Распознавание осей синфазности
Для обнаружения объектов на изображении существуют алгоритмы, основанные на вычислении локальных признаков с помощью операции свертки. Свёртка (convolution) представляет операцию, которая вычисляет признаки схожести одной функции с другой. Для измерения меры схожести используют специальные фильтры – ядра. Ядро – это матрица, которая проходит по изображению с определенным шагом, вычисляя (сворачивая) область проекции. В результате свертки изображения получают матрицу признаков, содержащую числовые значения. Сравнивая вычисленные значения со значением фильтра, делают вывод о вероятности наличия искомого признака в той или иной области изображения [5].

Рис. 5. Утончение области

Рис. 6. Распознавание гипербол, delta_conv = 0,9
В качестве фильтров свертки (kernels) в приложении выступают всевозможные варианты гипербол. Все фильтры были подготовлены и сохранены в растровом формате с расширением png. Каждый файл фильтра программа сохраняет в памяти в виде бинарных матриц, элементы которых равны единице в случае проекции теоретической гиперболы Gk, оставшаяся часть заполняется нулями:
kernelij = 1,
где kernelij∈Gk.
В результате свертки для каждой области m матрицы M вычисляются отклики Convm:
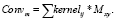
При некотором допустимом соотношении отклика Convm относительно количества единиц фильтра Convkernel делается вывод о наличии в данной области соответствующей гиперболической оси синфазности:
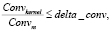
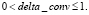
Коэффициент delta_conv предлагается устанавливать пользователям приложения. Обнаруженные оси синфазности закрашиваются красным цветом (рис. 6).
Как видно из рис. 6, на правом изображении программа распознала не все различимые глазом гиперболические оси. Данную проблему можно решить выбором меньшего коэффициента совпадения. Однако необходимо иметь в виду, что при установке меньшего допуска для delta_conv возможно обнаружение ложных образов гипербол. Поэтому данный параметр определяется опытным путем. Хорошие результаты были выявлены при установке delta_conv в пределах от 0,7 до 0,9 как на искусственных, так и на реальных изображениях радарограмм.
Заключение
Алгоритм, реализованный в приложении, позволил автоматизировать процесс обнаружения гиперболических осей синфазности, представленных на изображениях радарограмм дифрагированными волнами, отраженных сигналов от локальных объектов. Для распознавания был выбран метод, основанный на математической операции свертки. Успешность нахождения осей синфазности на реальных радарограммах в целом зависит от предварительной обработки изображения, а также от того, насколько ровной будет средняя линия, полученная при операции «утончения» областей.
В дальнейшем планируется добавить программные методы для спрямления средних линий на проблемных участках, что позволит увеличить процент распознанных полезных сигналов, представленных гиперболическими осями синфазности, а также уменьшит ошибки при определении их формы. Данный алгоритм был разработан для проведения опытного эксперимента и не претендует на полноту. Методика, предлагаемая в рамках статьи, может быть использована как вспомогательная при решении задач анализа и моделирования георадиолокационных данных.
Авторы выражают искреннюю признательность зав. лабораторией георадиолокации ИГДС СО РАН к.т.н. доценту Федоровой Ларисе Лукиничне за постановку задачи и оказанную помощь при проведении данного исследования.









