Моделирование пешеходных потоков приобрело огромную значимость в последние десятилетия, так как строительсто и проектирование мест притяжения большого количества людей требует создания условий безопасности. Многие модели взаимодействия людей в потоке основаны на аналогичных моделях для потоков транспортных средств. Однако движение пешеходов гораздо более неустойчиво, больше зависит от поведения отдельных индивидуумов. Кроме того, в отличие от транспортного потока, здесь допускаются «столкновения», пешеходы могут задевать друг друга при движении, и это не будет являться причиной инцидента или затора. Эти факты учитываются при микроскопическом моделировании. Кроме того, даже достаточно организованный поток, следующий в определенном направлении, часто разбивается на связанные пары или кластеры (группы знакомых, члены одной семьи и т.п.).
Классически по уровню детализации модели пешеходных потоков делят на:
- микроскопические, которые учитывают поведение каждого пешехода отдельно [1, 2];
- мезоскопические, учитывающие поведение отдельного пешехода, но с целью определения характеристик потока или его закона распределения [3, 4];
- макроскопические, которые описывают поток в терминах скорости, плотности, без учета поведения отдельных индивидуумов [5].
Экспериментально доказана также теория феномена самоорганизации пешеходного потока, который не планируется извне и не организуется внешним источником, таким как светофоры или поведенческие соглашения [2]. Особый интерес здесь представляют условия формирования:
- полосы движения в заданном направлении;
- реверсивные потоки в дверных проемах.
Отметим, что эти эффекты самоорганизации представляют собой модели поведения, которые не планируются извне, но неизбежно происходят по истечении определенного периода времени при движении потоков пешеходов.
Актуальной задачей является разработка математической модели, позволяющей с достаточной степенью точности определять параметры пешеходных потоков для управления ими в режиме реального времени.
Целью данной работы является разработка математической модели пешеходного потока как потока кластеров и метода определения параметров данного потока в режиме реального времени.
Материалы и методы исследования
В случае направленного движения пешеходов к переходу удобно применять модели, описывающие поток как случайный процесс с помощью случайных функций. Такую степень детализации данных относят к мезоскопической. Как отмечено выше, потоку пешеходов свойственно разделение на кластеры (группы родственников, знакомых и т.п.) [6]. Если описывать поток как поток случайных событий, то под событием будем понимать прибытие пешехода к точке плоскости с фиксированной координатой по оси, направленной вдоль двиижения потока. При этом прибытие к этой точке кластера следует интерпретировать как одно событие.
В модели TIMeR_Mod [7], разработанной автором, автотранспортный поток описывается как поток Пальма, интервалы по времени между которыми подчиняются обобщенному закону Эрланга. Подобного подхода будем придерживаться и при моделировании пешеходного потока.
Результаты исследования и их обсуждение
1. Алгоритм разбиения пешеходного потока среднего уровня плотности на кластеры
Видеодетекторы определяют мгновенные декартовы координаты (xi; yi) объектов (пешеходов) при съемке пешеходного потока сверху в локальной системе координат. Ось ОХ направлена по направлению движения пешеходного потока dfree – критическое значение расстояния между пешеходами, при котором их движение можно считать свободным.
1) вводим локальную систему координат для момента t = 0 и определяем координаты (xi; yi) объектов в этой системе;
2) формируем первый кластер:
2.1) начиная с левого нижнего угла (начало координат), определяем расстояния d1i от объекта номер 1 с координатами (x1; y1) до остальных объектов, входящих в прямоугольник, задаваемый ограничениями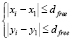 
:
;
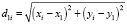2.2) если d1i ≤ dfree, то объекты P1 и Pi объединяем в один кластер;
2.3) берем следующий объект Pj из кластера 1 и определяем расстояния dji от объекта Pj с координатами (xj; yj) до остальных объектов, входящих в прямоугольник, задаваемый ограничениями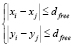 
:
;
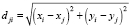2.4) если dji ≤ dfree, то объекты Pi включаем в первый кластер;
2.5) повторяем пункты 2.3 и 2.4 для всех объектов, входящих в первый кластер;
3) двигаясь вверх, вправо, вниз, вправо и т.д., формируем следующий кластер номер N:
3.1) берем объект Pn, не входящий ни в один кластер, и определяем расстояния dni от объекта Pn с координатами (xn; yn) до остальных объектов, входящих в прямоугольник, задаваемый ограничениями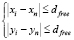 
:
;
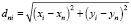3.2) если dni ≤ dfree, то объекты Pn и Pi объединяем в один кластер N;
3.3) берем следующий объект Pj из кластера N и определяем расстояния dji от объекта Pj с координатами (xj; yj) до остальных объектов, входящих в прямоугольник, задаваемый ограничениями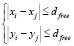 
:
;
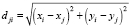3.4) если dji ≤ dfree, то объекты Pi включаем в кластер N;
3.5) повторяем пункты 3.3 и 3.4 для всех объектов, входящих в кластер N;
4) повторяем пункт 3 до тех пор, пока не разобъем все объекты, входящие в срез при t = 0 на кластеры;
5) для каждого кластера определяем центр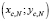 
; пусть 
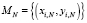– множество координат объектов Pi, N, входящих в кластер N; 
, 
, 
, 
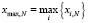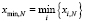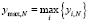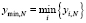. В этих обозначениях
.
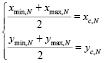2. Определение параметра λ интенсивности пешеходного потока
Определяем величины интервалов Ti по времени (в секундах) между прохождениями центров кластеров точки с фиксированной координатой по оси OX. Считая поток кластеров простейшим, определяем параметр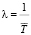 
, где 
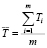– выборочная средняя случайной величины T.
В более общем случае при повышении плотности поток кластеров пешеходов может подчиняться (специальному) закону Эрланга. Тогда параметры распределения находятся следующим образом с помощью метода моментов [9]:
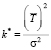, где σ2 – выборочная дисперсия случайной величины T;
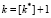– целое число, большее k*;
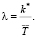
3. Определение параметров пешеходных потоков, прибывающих к данному пешеходному переходу по двум направлениям
Согласно проведенным исследованиям, поток кластеров пешеходов может быть аппроксимирован законом Эрланга порядков k = 1 (показательный закон) или k = 2. При более плотных потоках лучше не разбивать пешеходов на кластеры, а фиксировать интервалы по времени между отдельными пешеходами и ипользовать закон Эрланга при больших значениях k.
Плотность распределения Эрланга [8]:
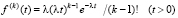; (1)
интегральная функция распределения Эрланга:
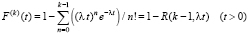. (2)
Пусть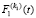 
– функция распределения первого потока кластеров пешеходов, а 
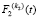– функция распределения первого и второго кластеров пешеходов. Вероятность того, что за время T** в первом потоке к данной точке не подойдет ни один кластер, равна
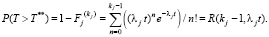(3)
Функция распределения минимума L случайных величин:
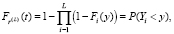(4)
где Fi(y) – закон распределения i-й величины.
Функция распределения времени, оставшегося до наступления очередного события (после случайного попадания точки в произвольный интервал между последовательными наступлениями событий) в потоке Эрланга порядка ki имеет вид [9]:
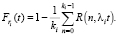(5)
Тогда функция распределения минимальной из L случайных величин определяется по формуле
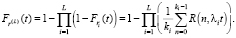(6)
А ее плотность распределения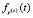 
:
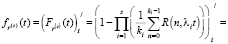
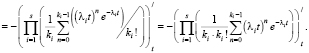(7)
Вероятность того, что за время T** во всех L потоках не произойдет ни одно событие:
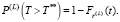(8)
Теперь определим среднее значение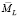 
минимальной из L случайных величин 
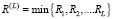. При вычислении интеграла воспользуемся формулой интегирования по частям:
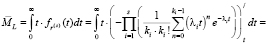
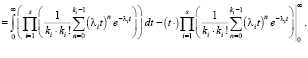(9)
В частности, найдем математическое ожидание случайной величины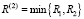 
:
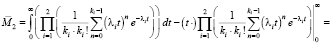
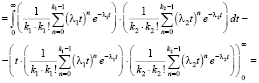
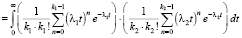
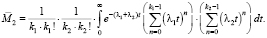(10)
При вычислении интеграла мы учли формулу интегрирования по частям, а при вычислении предела воспользовались арифметическими свойствами пределов функций и тем, что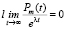 
, где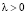 
, 
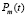– многочлен.
Обозначим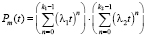 
– многочлен степени 
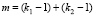переменной t. В общем случае будем считать 
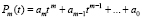и рассмотрим неопределенный интеграл:
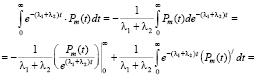
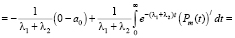
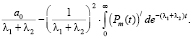(11)
В многочлене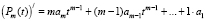 
свободный член равен 
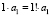. В многочлене 
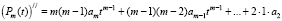свободный член равен 
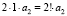. И так далее рассуждая, по индукции получим, что в многочлене 
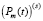свободный член 
.
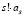Продолжим вычислять интеграл, учитывая при вычислении пределов следующее:
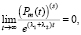
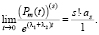(12)
Получим
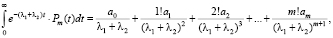
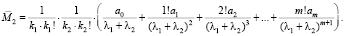(13)
4. Показатели для частных случаев распределений пешеходных потоков
Пусть к переходу с двух сторон стекают два пешеходных потока. Используя выведенные формулы (6), (7), (10) и (13), получим результаты для наиболее часто встречающихся на практике частных случаев:
1) оба потока кластеров пешеходов распределены по показательным законам с параметрами λ1 и λ2 соответственно (то есть k1 = k2 = 1):
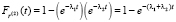– интегральная функция распределения интервалов R(2) между двумя последовательными прибытиями пешеходов к перекрестку (безразлично, в каком направлении);
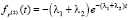– плотность распределения величины R(2);
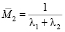– математическое ожидание величины R(2).
2) оба потока кластеров пешеходов распределены по закону Эрланга с параметрами λ1 и λ2 соответственно и k1 = k2 = 1:
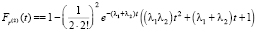– интегральная функция распределения величины R(2);
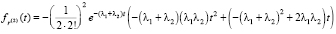– плотность распределения величины R(2);
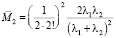– математическое ожидание величины R(2).
Заключение
В данной статье разработан алгоритм автоматизированного разбиения пешеходов в потоке на кластеры и метод определения параметров случайного потока в этом случае. Аналитический аппарат, полученный в пунктах 3 и 4, позволяет определять параметры пешеходных потоков, прибывающих к пешеходному переходу. Причем результат получается в режиме реального времени, что позволяет применять модель в интеллектуальных транспортных системах.