Анализ тенденций развития современной теории и техники автоматического управления техническими объектами позволяет определить перспективные направления научных исследований. Развитие теории и практики формирования нечётких логических алгоритмов управления, основанных на использовании знаний, опыта, логики, интуиции и эвристики исследования, является актуальным для решения многих прикладных задач автоматического управления техническими объектами.
При недостаточной информации об объекте, изменении случайным образом параметров объекта, при управлении нелинейными или сложными объектами, при управлении объектами, обладающими свойствами уникальности, традиционные ПИД-регуляторы (hard – computing) не позволяют добиться высокого качества управления. В последнее десятилетие наметилась тенденция замены классических линейных регуляторов нечёткими регуляторами [1, 2].
Аппарат теории нечётких множеств предложил Л. Заде в 1965 г., а применение этой теории для построения систем с нечёткими регуляторами показал в 1974 г. Мамдани. Преимуществами нечётких регуляторов (soft – computing) являются: обеспечение требуемого качества управления объектами при внешних и внутренних возмущениях путём изменения передаточного коэффициента регулятора на разных этапах переходного процесса, простая реализация программными методами, возможность минимизации среднеквадратического отклонения (СКО) при стабилизации стационарного режима работы системы, возможность изменять параметры нечёткого регулятора без изменения программы в целом. Основной недостаток нечётких контроллеров – сложность настройки (нормализация, фаззификация, составление базы нечётких правил, нечёткий вывод, дефаззификация, денормализация). Целостных и законченных методик синтеза алгоритмов нечёткого вывода на базе продукционных правил, позволяющих реализовать нечёткое управление в соответствии с требуемыми критериями функционирования автоматических систем, к настоящему времени не существует.
Материалы и методы исследования
Покажем методику настройки нечёткого регулятора с нелинейной характеристикой Р-типа средствами Matlab [3] на следующем примере.
Пусть передаточная функция объекта управления имеет вид
,
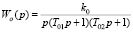где ko = 2, T01 = 0,2 с, T02 = 1 с. Управление объектом осуществляется на основе фундаментального принципа по отклонению контролируемой функции от входного воздействия (принцип Ползунова – Уатта). Система при единичной отрицательной обратной связи и передаточном коэффициенте регулятора kрег = 3 находится на границе устойчивости. Если применить традиционный ПИД-регулятор с передаточными коэффициентами, рассчитанными по методу Зиглера – Никольса (с дополнительной поднастройкой), [4] kр = 0,6, ki = 0,714286, kd = 0,35, то система работает устойчиво с показателями качества tр = 10,7 с, σ = 52,5 %, δстат = 0.
В нечётких контроллерах воплощено желаемое состояние объекта управления и требуемое качество работы системы. В приведенной схеме нечёткий регулятор используется для непосредственного (прямого) управления объектом. Нечёткий логический вывод (блок формирования логических решений – inference) основан на использовании нечётких входных переменных (лингвистических переменных) и нечётких правилах преобразований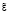 
в 
.
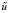Для стабилизации работы системы с требуемыми показателями качества нечёткий Р-регулятор должен формировать нелинейный закон управления [5, 6].
Введём аксиоматические требования к поверхности отклика нечёткого статического регулятора:
1. Выполнить формирование поверхности отклика регулятора, обеспечивающей плавность процесса управления.
2. Для стабилизации работы системы в районе нуля входной переменной ε статический передаточный коэффициент регулятора выполнить меньше единицы.
3. С целью уменьшения времени переходного процесса в районах, где входная переменная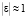 
, статический передаточный коэффициент регулятора установить больше единицы.
4. Нелинейный закон управления объектом должен содержать пять участков, что предопределяет минимальное количество термов (семь), ибо типовой переходный процесс содержит три участка (разгон, торможение, стабилизация) при положительных и отрицательных значениях рассогласования, а нечёткое описание позволяет сгладить переходы от одного участка к другому.
5. Стратегия управления объектом: при запуске системы коэффициент усиления регулятора повышается, уменьшая время переходного процесса, при приближении выходной функции к требуемому значению передаточный коэффициент резко снижается, уменьшая перерегулирование и стабилизируя работу системы.
Алгоритм синтеза нечёткого нелинейного регулятора Р-типа следующий:
1. В линейном нечётком регуляторе Р-типа формируем лингвистические переменные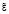 
и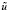 
с семью термами с базовыми настройками в Matlab и семью продукционными правилами «вход – выход» (знак управления совпадает со знаком ошибки).
2. Линейный нечёткий Р-регулятор преобразуем в нелинейный путём смещения центров и координат оснований функций принадлежностей входной лингвистической переменной с целью уменьшения времени переходного процесса и установки в координату ноль универсального множества центра функции принадлежности tf 4 с параметрами основания, охватывающего универсальное множество [-1,1] для стабилизации работы системы.
3. Устанавливаем тип нечёткой системы – Мамдани.
4. Формируем базу правил и изменяем параметры функций принадлежности так, чтобы статическая характеристика нечёткого регулятора соответствовала аксиоматическим правилам и переходный процесс формировался быстро затухающим устойчивым.
5. Проверка работоспособности системы и настройка регулятора производятся на модели системы в графическом редакторе Simulink, встроенном в информационную систему Matlab.
6. Если по каналам управления и возмущения наблюдаются недопустимые статические ошибки, то на выходе нечёткого регулятора устанавливается ПИ-регулятор.
Конкретизируем методику синтеза (механизм выбора) нечёткого нелинейного P-регулятора управления объектом, используя возможности развивающейся информационной среды Matlab.
Стратегия управления отображается в формируемых лингвистических переменных и базе правил. Вырабатывается тактика управления по графикам переходных характеристик и статическим характеристикам регулятора. Графики разбиваются на зоны (участки). Проводится анализ лингвистических переменных и продукционных правил на каждом участке и вырабатывается требуемое управляющее воздействие. Графики характеристик «выход – вход» нечёткого регулятора выводятся в браузере SurfaceViewer.
Сформируем лингвистические переменные входного воздействия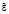 
и выходной функции 
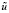. Примем количество термов лингвистических переменных равным 7. Форма функций принадлежности выбирается, исходя из смысла решаемой задачи. В [1, 3] показано, что в системах автоматического управления с нечёткими регуляторами предпочтительно использовать треугольные функции принадлежности [7]. Используем тип функции принадлежности trimf (треугольный) на универсальном множестве [-1,1]. Названия термов, имя и базовые параметры функций принадлежности приведены в табл. 1.
Экспертный закон управления, составленный в виде связей между лингвистическими метками входного воздействия и термами регулирующего воздействия на начальном этапе синтеза нечёткого регулятора, приведен в табл. 2.
Построим в программной среде Simulink модели систем с ПИД-регулятором и с нечётким регулятором (рис. 1).
Настройку параметров функций принадлежностей входной лингвистической переменной и формирование базы правил осуществим в следующей последовательности.
Эксперимент № 1
Параметры функций принадлежности входной и выходной лингвистических переменных (базовые в Matlab) приведены в табл. 1. База знаний формируется по данным табл. 2.
Таблица 1
Названия термов, имя и базовые параметры функций принадлежности
|
Названия функций принадлежности |
Имя функции принадлежности |
Базовые параметры в MATLAB |
|
LN – large negative |
mf1 |
[-1,333 -1 -0,6667] |
|
MN – medium negative |
mf2 |
[-1 -0,6667 -0,3333] |
|
SN – small negative |
mf3 |
[-0,6667 -0,3333 -5,55e-17] |
|
Z – zero |
mf4 |
[-0,333 0 0,333] |
|
SP – small positive |
mf5 |
[-5,55e-17 0,3333 0,6667] |
|
MP – medium positive |
mf6 |
[0,3333 0,6667 1] |
|
LP – large positive |
mf7 |
[0,6667 1 1,333] |
Таблица 2
Экспертные решения исходного состояния нечёткого регулятора
|
|
LP |
MP |
SP |
Z |
SN |
MN |
LN |
|
LP |
v |
||||||
|
MP |
v |
||||||
|
SP |
v |
||||||
|
Z |
v |
||||||
|
SN |
v |
||||||
|
MN |
v |
||||||
|
LN |
v |
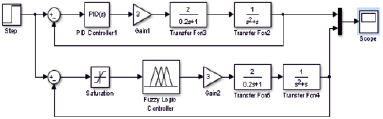
Рис. 1. Модели систем с ПИД-регулятором (верхняя часть рисунка) и с нечётким регулятором (нижняя часть рисунка)
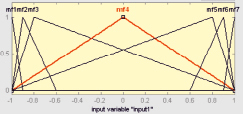
Рис. 2. Функции принадлежности входной лингвистической переменной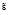 
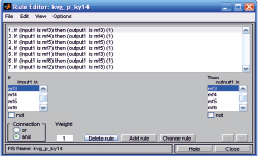
Рис. 3. База правил настроенного нечёткого нелинейного регулятора Р-типа
Эксперимент № 2
Вводим следующие изменения координат оснований и вершин функций принадлежности входной лингвистической переменной: [-1,1 -1 -0,9]∈mf1, [-1 -0,9 -0,6]∈mf2, [-0,9 -0,6 0]∈mf3, [-0,6 0 0,6]∈mf4, [0 0,6 0,9]∈mf5, [0,6 0,9 1]∈mf6, [0,9 1 1,1]∈mf7.
Эксперимент № 3
Изменим параметры функций принадлежности: [-1 -0,8 1]∈mf3, [-1 0 1]∈mf4, [-10,81]∈mf5. Остальные функции принадлежности с теми же параметрами, что и в предыдущем эксперименте. Введём изменения в базу правил: ЕСЛИ mf1, ТО mf2, ЕСЛИ mf7, ТОmf6.
Эксперимент № 4
Параметры функций принадлежности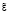 
(рис. 2) оставляем теми же, что и в эксперименте № 3, но изменяем базу правил, приведенную на рис. 3.
Результаты исследования и их обсуждение
В результате эксперимента № 1 получили, что статическая характеристика регулятора близка к линейной с передаточным коэффициентом близким к единице, переходная характеристика – периодические синусоидальные колебания (система на границе устойчивости). Эксперимент № 2 показал, что статическая характеристика регулятора на базовом множестве [-0,5; 0,5] близка к линейной, передаточный коэффициент на этом участке меньше единицы, переходная характеристика – процесс устойчив, слабо затухающего характера. В ходе эксперимента № 3 выявили, что статическая характеристика регулятора на базовом множестве [-0,6; 0,6] близка к линейной, передаточный коэффициент на этом участке стал меньше, чем в эксперименте № 2, в диапазонах [-1; -0,4] и [0,6; 1] базового множества статическая характеристика близка к линейной с большим передаточным коэффициентом, переходная характеристика – процесс устойчив, быстро затухающего характера с показателями качества σ = 63,4 %, tp = 7,37 c, N = 1. На завершающем этапе эксперимент № 4 позволил привести статическую характеристику в требуемый вид – характеристика изображена на рис. 4, переходная характеристика приведена на рис. 5, показатели качества соответствуют требуемым значениям σ = 37,2 %, tp = 7,35 c, N = 1.
Заключение
В ходе исследования выявили, что для стабилизации работы системы необходимо изменить настройки нечёткого регулятора. Введенные изменения в параметры функций принадлежности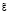 
в эксперименте № 2 оказались эффективны, и возникла необходимость продолжать изменение параметров в этом направлении, добиваясь улучшения качества работы системы. После изменения параметров функций принадлежности mf3 и mf4 получили неприемлемую величину перерегулирования σ = 63,4 %. Для его снижения уменьшили передаточный коэффициент регулятора вне средней зоны базового множества и получили требуемые статическую характеристику нечёткого нелинейного регулятора Р-типа (рис. 4) и переходные характеристики системы с ПИД-регулятором и с нечётким регулятором (рис. 5).
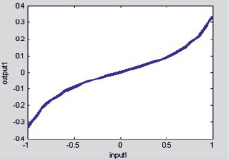
Рис. 4. Статическая характеристика нечёткого нелинейного регулятора Р-типа
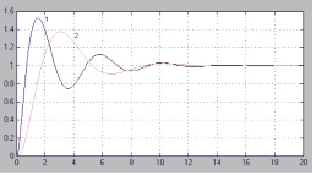
Рис. 5. Переходные характеристики системы с ПИД-регулятором (кривая 1) и с нечётким регулятором (кривая 2)