Моделирование риска обычно включает в себя выделение опасных исходов, количественное задание последствий от их наступления и оценку их вероятностей [1]. Вклад различных рисков объединяют и рассматривают одномерную случайную величину [2–4]. Однако у такой модели есть недостатки. Во-первых, не всегда известны заранее все возможные опасные исходы и, соответственно, мы не знаем их вероятности. Во-вторых, реальные системы обычно имеют много различных факторов риска. А поскольку они могут быть взаимосвязанными, то необходимо факторы риска рассматривать совместно, т.е. возникает потребность в многомерном моделировании риска.
В [5] предложен подход к моделированию многомерного риска. Он был реализован для распространенного случая гауссовских систем [6]. Однако реальные объекты (например, в медицине и региональной экономике) не всегда удается адекватно описать в виде гауссовских систем. Это часто вызвано неоднородностью исследуемой выборочной совокупности, в которой могут присутствовать несколько выраженных однородных подмножеств, каждое из которых может быть описано гауссовским случайным вектором. В этом случае, как показали результаты моделирования, рассмотрение всей выборки в виде однородной гауссовской системы может приводить к значительным ошибкам при оценивании риска. Поэтому необходимо в модели риска учесть негауссовость системы.
Целью статьи является описание новой модели многомерного риска, в которой стохастическая система описывается в виде совокупности нескольких взаимно независимых гауссовских систем, для каждой из которых определяется или задается вероятность (доля) ее присутствия в исследуемой совокупности. Будет подробно рассмотрен случай, когда исследуемая выборка формируется из совокупности двух гауссовских систем.
Материалы и методы исследования
Рассмотрим неоднородную стохастическую систему S. Выделим в ней M факторов риска Xj и будем считать их компонентами случайного вектора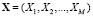 
. В отличие от [6], когда X представлял собой гауссовский случайный вектор, рассмотрим более общий случай 
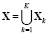, где все случайные векторы Xk являются гауссовскими с соответствующими распределениями 
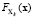. Функция распределения случайного вектора X может быть представлена как
,
, 
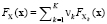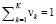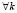
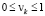. (1)
Представление (1) позволяет учесть неоднородность стохастических систем. Действительно, мы фактически здесь имеем совокупность K подмножеств (кластеров). Например, в популяции могут быть как здоровые, так и больные люди, при рассмотрении регионы также могут делиться на несколько групп (кластеров) и т.д.
Неблагоприятные исходы описываем в виде геометрической области, вид которой определяется конкретной системой, решаемой задачей и априорных сведений. Для определенности опишем предлагаемый подход на примере распространенной концепции нежелательных событий как больших и маловероятных значений случайного вектора X. Тогда вероятность неблагоприятного исхода для случайного вектора X равна [5]
,
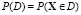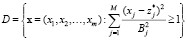, (2)
где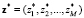 
– некоторое наиболее безопасное значение, Bj – пороговые уровни.
Очевидно, когда исход не лежит на одной из осей, то событие D может реализоваться и при отсутствии рисковых отклонений по всем компонентам (например, возможны ситуации, когда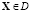 
и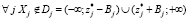 
). Риск оценим как [5]
,
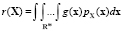где pX(x) – плотность вероятности случайного вектора X, g(x) – функция последствий от опасных ситуаций. Задав
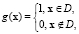(3)
получим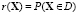 
, т.е. риск будет равен вероятности возникновения неблагоприятного исхода. Оценка (3) хорошо интерпретируется, а также является удобным начальным приближением модели риска на ранней стадии исследования системы, когда сложно достаточно точно описать функцию g(x).
Результаты исследования и их обсуждение
Одной из проблем при использовании модели (1) является определение параметров распределений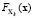 
и вероятностей nk. Ниже рассмотрим варианты решения на примере двух кластеров. Во-первых, можно воспользоваться дискриминантным анализом. Для реализации алгоритма поиска параметров необходимо знать вероятность принадлежности очередного наблюдения тому или иному кластеру. Дискриминантный анализ на основе логистической регрессии [7] позволяет оценить эти вероятности. Алгоритм разыгрывания для оценки параметров распределений кластеров состоит в следующем.
Вход: data – массив координат входных объектов; probas – вероятности принадлежности к кластерам каждой точки (длина массива равна длине массива data), N – количество розыгрышей, K – количество кластеров.
Выход: параметры распределений каждого кластера.
Шаг 1. Вычисляем кумулятивную сумму для векторов вероятностей в кластерах для каждой точки, установить счетчик равным 0.
Шаг 2. Разыгрываем случайную величину p, равномерно распределенную на [0; 1).
Шаг 3. Для всех точек определяем по кумулятивному вектору вероятностей, в какой кластер соотносится точка. Номер кластера будет определяться индексом минимального значения элементов вектора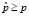 
.
Шаг 4. Выделяем из всего набора данных кластеры, полученные на шаге 3.
Шаг 5. Вычисляем оценки математических ожиданий и дисперсий для каждого кластера и записываем результаты, увеличиваем счетчик на 1.
Шаг 6. Если счетчик меньше N повторяем шаги 2–5, иначе вычисляем оценки математических ожиданий и дисперсий по N опытам. Усредненные по всем опытам оценки будут результатом оценки параметров.
Стоит отметить, что описанный алгоритм является частным случаем для двух кластеров и его можно расширить для любого конечного числа кластеров, вместо разыгрывания одной случайной величины p будем разыгрывать вектор вероятностей p, состоящий из K – 1 элементов. Тогда попадание на основе этих значений наблюдений в тот или иной кластер будет описываться мультиномиальным распределением. Остальные шаги процедуры останутся неизменными.
Также можно использовать модель смеси гауссиан (GMM) [8]. GMM реализуется с помощью решения оптимизационной задачи максимального правдоподобия (Expectation Maximization) [9]. EM-алгоритм – общий метод нахождения оценок функции правдоподобия в моделях со скрытыми переменными. В данной статье рассматривается интерпретация смеси гауссовых распределений в терминах дискретных скрытых переменных.
Помимо того что смеси распределений позволяют приближать сложные вероятностные распределения, с их помощью можно также решать задачу кластеризации данных. Далее мы будем решать задачу кластеризации с помощью ЕМ-алгоритма, предварительно приблизив решение алгоритмом k-средних [10].
Сравнительный анализ оценок параметров распределения кластеров показал, что оба алгоритма (на основе логистической регрессии и GMM) дали сравнимые по точности результаты.
Проведем расчет риска неоднородных систем с двумя кластерами. Рассмотрим пять модельных случаев систем из двух совокупностей, число компонент M = 2: 1 – каждая компонента имеет диагональную ковариационную матрицу; 2 – «вытянутые» рассеяния; 3 – каждая компонента состоит из коррелированных параметров; 4 – компоненты каждой из совокупности зависимы, между ними значимые пересечения; 5 – «непересекающиеся» классы. Методика эксперимента состояла в следующем.
Генерируем данные для модельных случаев с заданными параметрами – известными ковариациями и математическими ожиданиями. На всех модельных примерах доли совокупностей одинаковы, то есть вероятность попадания случайного наблюдения равна 0,5 для одного случая. Посмотрим, как эти доли могут влиять на значения риска. Для каждого из случаев заранее известны параметры распределений каждой совокупности – векторы средних и ковариации (в силу того что считаем каждую из совокупностей представимой в виде гауссовского случайного вектора). В каждом из модельных примеров одна из совокупностей будет считаться «благоприятной», а границы области будут определяться эллипсом. Будем проводить эксперимент следующим образом:
1) для каждого случая по известным параметрам сгенерируем по 30 пар совокупностей;
2) для каждого случая и каждой из 30 итоговых выборок попытаемся восстановить параметры двумя способами – с помощью алгоритма на основе логистической регрессии, а также с помощью EM-алгоритма (GMM-модель);
3) на основе восстановленных параметров сгенерировать достаточное количество наблюдений каждой совокупности;
4) методом Монте-Карло выполнить расчет вероятности непопадания в благоприятную область. Это и будет вероятностью риска в системе.
Поскольку на модельных примерах имеется информация об исходных параметрах распределений каждой совокупности, можно с высокой точностью оценить реальный риск. Также приведем расчет риска заданной системы, представленной в виде однородной гауссовской системы [5], и проведем расчет с восстановленными логистической регрессией и GMM параметрами.
На рис. 1–5 благоприятная область отмечена эллипсом, благоприятные точки – точками, а неблагоприятные точки – крестиком. Вероятность риска – это отношение числа пересечений к общему числу наблюдений.
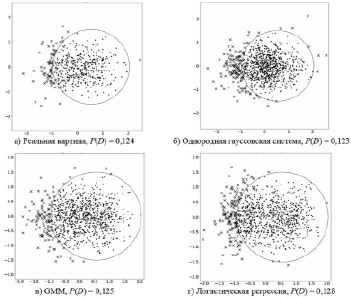
Рис. 1. Каждая компонента имеет диагональную ковариационную матрицу
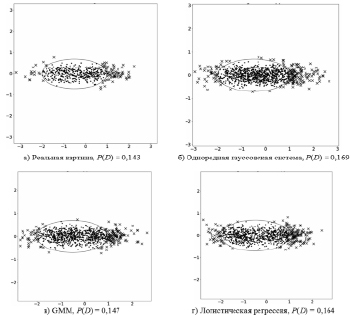
Рис. 2. «Вытянутые» рассеяния
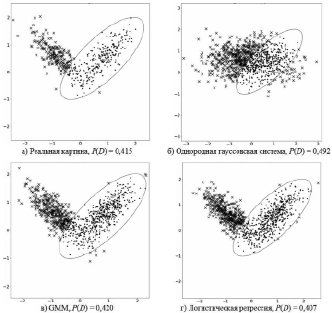
Рис. 3. Каждая компонента состоит из коррелированных параметров
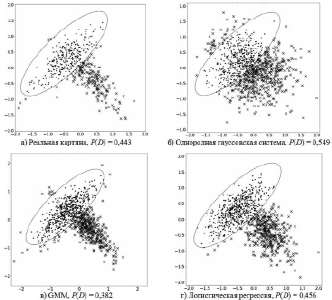
Рис. 4. Компоненты каждой из совокупности зависимы, между ними значимые пересечения
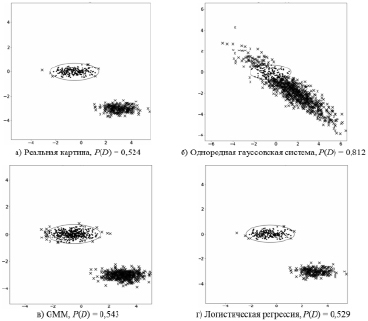
Рис. 5. «Непересекающиеся» классы
Анализ данных примеров показывает, что в четырех случаях из пяти использование модели в виде однородной гауссовской системы привело к значительному завышению оценки риска. Несмотря на то что для первых двух случаев (рис. 1, 2) нет выигрыша в точности оценки риска, снижения качества также не наблюдается. В остальных же случаях (рис. 3–5) использование модели для неоднородной системы предпочтительнее, поскольку результаты расчета рисков более приближены и сравнимы с реальными показаниями, в то время как однородная модель существенно завышает эти показатели.
Выводы
1. Показано, что представление неоднородных систем в виде гауссовского случайного вектора может приводить к значительным ошибкам в оценке риска.
2. Предложена модель многомерного риска для неоднородных стохастических систем. При этом система представляется в виде совокупности гауссовских случайных векторов.
3. Предложен и рассмотрен алгоритм для восстановления параметров распределения на основе вероятностей принадлежности каждой точки. В статье использовалась логистическая регрессии. Однако можно использовать и другие методы классификации.
4. GMM по сравнению с логистической регрессией имеет меньшую стабильность в расчете рисков, поэтому предпочтительнее использовать поиск параметров с помощью логистической регрессии. Но последний алгоритм вычислительно более затратен и требует некоторую информацию об исходных совокупностях в виде обучающей выборки.
Работа выполнена при финансовой поддержке гранта РФФИ, проект № 20-51-00001.