Одной из важных задач математической и компьютерной химии является задача поиска количественных соотношений между структурой и свойствами химических соединений. Для математических моделей связи «структура-свойство» такого вида в литературе часто используется аббревиатура QSPR/QSAR (Quantitative Structure-Property/Activity Relationships), зависящая от того, какое свойство соединений рассматривается – физико-химическое или какая-либо биологическая активность [1–3]. Моделирование такого вида является очень популярным в различных областях химии (в частности, в медицинской и фармацевтической химии, в химии полимеров, в компьютерном дизайне лекарств и т.д.) [4–6]. Найденные количественные соотношения между структурой и свойствами соединений позволяют осуществлять прогноз свойств веществ (как реально существующих, так и гипотетических) по их структуре при помощи соответствующих расчетов, что может быть использовано для целенаправленного поиска соединений с заданным набором свойств. Следует отметить, что к настоящему времени синтезировано огромное количество химических веществ (примерно 140 миллионов). Однако экспериментальное определение их различных свойств с целью поиска соединений с нужными свойствами является во многих случаях весьма затруднительным с технической точки зрения и, кроме того, требует существенных финансовых и временных затрат. В связи с этим разработка и тестирование различных математических методов моделирования связи между структурой и свойствами химических соединений является актуальной задачей [7–9].
Любое исследование в области построения и исследования QSPR/QSAR-моделей начинается с выбора способа построения математической модели молекулы. Наиболее часто структуру молекулы описывают при помощи меченого или взвешенного графа. Обычно вершины и ребра таких графов соответствуют атомам и химическим связям в молекуле, однако вершины графа могут соответствовать и целым структурным фрагментам молекулы. Символьные метки, приписанные вершинам (и / или ребрам) такого графа, позволяют на качественном уровне различать атомы (связи) различной химической природы. Приписывая вершинам и ребрам графа числовые веса, можно заложить в такую графовую модель молекулы количественную информацию о каких-либо физико-химических характеристиках соответствующих атомов и связей. Подчеркнем, что классическая структурная формула молекулы – это пример вышеописанного графа с символьными метками вершин и основа для построения других вариантов молекулярных графов [10; 11]. Таким образом, на данном этапе исследований возникает проблема выбора способа представления химической структуры в виде графа.
Для количественного описания структуры молекулярного графа могут быть использованы какие-либо его числовые инварианты (т.е. числа, определяемые по графу по какому-либо общему алгоритму, не зависящие от способа нумерации его вершин). Примерами инвариантов являются определитель матрицы графа (для графов с числовыми весами), число определенных структурных фрагментов (их можно вычислять как для графов с символьными метками, так и с числовым весами) и т.д. Инварианты молекулярных графов широко используются в моделях связи «структура-свойство» как количественные молекулярные дескрипторы. Отметим, что в теоретической и математической химии инварианты графов обычно называют топологическими индексами [10; 11]. Молекулярные дескрипторы такого типа удобны тем, что они могут быть найдены непосредственно по структуре молекулы, в отличие, например, от дескрипторов, равных значениям каких-либо физико-химических свойств соответствующих молекул. Однако инвариантов графов существует бесконечно много, и, следовательно, на этом этапе исследований возникает проблема выбора подходящего набора инвариантов для описания структуры графа.
Итак, пусть некоторое свойство химических соединений (физико-химическое или биологическая активность) может быть измерено количественно. Пусть известны значения y1,…,yN этого свойства для некоторых N химических соединений, представленных структурными формулами. Предположим, что эти соединения каким-то образом представлены в виде молекулярных графов и выбран набор инвариантов x1,…,xn этих графов, характеризующих структуру соответствующих молекул. Тогда модель связи «структура-свойство», построенная по исходным данным, представляет собой приближенное уравнение вида y = F(x1,…,xn), связывающее значения параметров x1,…,xn и величину y изучаемого свойства при помощи некоторой функции F. Эта функция подбирается так, чтобы данное уравнение было бы как можно более точным на исходном наборе химических соединений (часто называемом обучающей выборкой соединений). На этом этапе исследований возникает проблема выбора подходящей функции F. Наиболее часто в качестве функции F используется линейная функция; при этом коэффициенты в ней подбираются по обучающей выборке при помощи стандартного метода наименьших квадратов.
Качество построенной модели можно оценивать разными способами [8]. Например, при помощи полученного уравнения можно рассчитать значения свойств соединений исходной выборки, а также некоторой тестовой выборки соединений, которая не использовалась в построении модели, и затем оценить точность этих расчетов. Для характеристики этой точности, как правило, используются такие статистические параметры регрессионного уравнения, как коэффициент корреляции R и среднеквадратичное отклонение s (возможно использование и других параметров, например величины средней относительной ошибки в процентах, и т.д.). Если тестовая выборка отсутствует, то для оценки качества модели к исходной выборке можно применить так называемую процедуру cross-validation. Согласно этой процедуре из исходного множества соединений выбрасывается одно соединение, затем для оставшихся N-1 соединений строится модель на основе ранее выбранных параметров. Далее осуществляется прогноз свойства исключенного соединения. Эта процедура повторяется для всех соединений исходной выборки. Затем строится корреляция между экспериментальными и расчетными значениями свойств всех соединений, для которой определяются коэффициент корреляции Rcv и среднеквадратичное отклонение scv .
При вышеуказанном моделировании возникает вопрос об оптимальном выборе числа параметров n при фиксированном объеме исходной выборки N (или о соотношении N:n). Эта проблема связана с тем, что практически всегда можно построить корреляцию с R = 1, используя в уравнении ровно N параметров. Однако прогнозирующая способность такой модели для соединений тестовой выборки будет невысока. В настоящее время нет никаких теоретически обоснованных правил выбора соотношения N:n, имеются лишь некоторые общие рекомендации в этой области, основанные на собственном практическом опыте ряда исследователей (см., например, [8]). Однако, как отмечается в [8], в любом случае при построении модели надо стремиться к тому, чтобы соотношение N:n было бы как можно больше, так как это, как правило, ведет к расширению области применимости модели.
Цель исследования – разработка, описание и тестирование ряда общих методов поиска QSPR/QSAR-моделей в рамках статистического подхода к математическому моделированию связи между строением и свойствами химических соединений. При этом предполагается, что некоторый способ представления химических структур в виде графов уже выбран. Специфика предлагаемых методов заключается в определенном выборе молекулярных дескрипторов, а также в методике поиска аппроксимирующей функции в искомом уравнении связи «структура-свойство».
Методы построения QSPR/QSAR-моделей
Предположим, что уже выбран некоторый способ представления химических структур в виде меченых (или взвешенных) графов. Обсудим вопрос выбора инвариантов x1,…,xn построенных молекулярных графов, которые далее предполагается использовать в качестве дескрипторов молекулярных структур в искомых уравнениях связи «структура-свойство». Пусть p – это максимальное число вершин в молекулярных графах заданного набора. Рассмотрим подграфы этих графов следующего вида: они имеют m вершин (1 ≤ m ≤ p) и состоят из объединения следующих изолированных фрагментов: изолированных вершин, цепочек длины один (т.е. ребер), циклов, цепочек длины большей, чем два. При построении этих подграфов учитываются метки вершин и ребер. Выбор именно таких подграфов связан с тем, что по подграфам такой структуры однозначно восстанавливаются собственные числа и собственные векторы взвешенного графа, а по ним – матрица графа, т.е. сам граф [12]. Таким образом, набор подграфов вышеуказанного вида несет в себе довольно большую информацию о структуре графа. Будем использовать в качестве молекулярных дескрипторов инварианты, равные числам вхождения в граф таких подграфов. Заметим, что для решения поставленной задачи можно использовать не все возможные подграфы такого вида, а какую-либо небольшую их часть.
Рассмотрим теперь вопрос о выборе функции F. Ее подбирать можно разными способами.
Далее представлены 2 возможных способа такого построения.
Метод 1. Выберем некоторые k инвариантов из множества всех базовых инвариантов (рассматриваемых в данной задаче), которые дают наилучшую линейную k-параметрическую модель (k – фиксированное число, k < N, где N – общее число соединений в обучающем множестве). Для этой цели можно использовать, например, хорошо известный метод пошаговой линейной регрессии. Будем улучшать эту модель, при условии, что новая модель, являющаяся линейной относительно некоторых новых параметров, тоже содержит k параметров. На основе выбранных инвариантов построим новые инварианты, равные их всевозможным попарным произведениям и квадратам. Рассмотрим множество, состоящее из исходных k инвариантов и новых 0.5(k2 + k) инвариантов. Выберем теперь из этого множества k инвариантов, дающих наилучшую линейную модель связи «структура-свойство». Как правило, получаемая модель оказывается точнее предыдущей. К отобранному набору k инвариантов опять применим описанную выше процедуру, стремясь получить более точную модель, и т.д. Этот процесс заканчиваем, когда его очередной шаг не приводит к улучшению модели или уже получена требуемая точность модели. Процесс можно закончить и тогда, когда получена модель той же точности, что и исходная, но с меньшим числом параметров. Таким образом, в данном подходе аппроксимирующая функция F представляет собой многочлен от нескольких переменных (при этом число переменных может оказаться меньше k).
Метод 2. Предположим, что для построения модели из некоторого заданного множества базовых инвариантов мы отбираем наилучшие k параметров (k-фиксированное число), используя метод пошаговой линейной регрессии, последовательно добавляя в уравнение регрессии параметры по одному. Проведем следующую процедуру построения новой модели, состоящую из k последовательных шагов, используя уже отобранные k параметров. Предположим, что на i-м шаге процедуры методом пошаговой линейной регрессии из данного множества параметров выбран некоторый, наилучший параметр x (i = 1,…,k). Затем мы последовательно проверяем, не будет ли параметр xt при некотором t = 2,3,… лучше, чем параметр хt-1. После того как найдено такое максимальное значение t, мы аналогичным образом тестируем параметры xt при t = 1/2,1/4, 1/8… и затем выбираем среди всех вариантов наилучший. При этом можно рассматривать и некоторые промежуточные значения показателя степени t. Новый параметр xt включаем в уравнение регрессии вместо х. Далее выбираем наилучший из оставшихся базовых параметров и выполняем с ним аналогичные действия. Процедура заканчивается, когда полученная модель будет содержать k параметров.
Отметим, что при построении модели возможна и комбинация этих двух подходов, описанных выше. Для некоторого промежуточного набора параметров на одном этапе для улучшения модели можно использовать метод 1, а на другом – метод 2.
Некоторые примеры приложения предложенных методов
Для реализации и исследования эффективности описанных выше методов конструирования QSPR/QSAR-моделей были использованы некоторые данные по структурам и свойствам (биологической активности разных видов) химических соединений. В ряде случаев было проведено сравнение результатов, полученных предлагаемыми методами и некоторыми другими известными методами, примененными к тем же самым данным. Далее будем обозначать через N число химических структур, используемых для построения модели связи «структура-свойство» (МССС). Пусть R и s – коэффициент корреляции и среднеквадратичное отклонение для линейной регрессии, соответственно, Rcv и scv аналогичные параметры, полученные в так называемой процедуре кросс-валидейшн (cross-validation), используемой для проверки стабильности модели.
Пример 1. Хорошо известно, что галогензамещенные углеводороды (содержащие атомы F, Cl) имеют наркотическую активность. Типичный представитель соединений этого класса – это хлороформ (CHCl3) [13]. Рассмотрим следующее множество N = 15 соединений, которые являются галогензамещенными метана и этана:
1) CHFClCHFCl; 2) CFCl2CHFCl; 3) CHCl3; 4) CF2ClCHCl2; 5) CFCl2CH2Cl; 6) CH2Cl2; 7) CHF2CH2Cl; 8) CF3CHCl2; 9) CF2ClCHFCl; 10) CHFCl2; 11) CFCl2CH3; 12) CF3CHClF; 13) CHF2Cl; 14) CF2ClCH3; 15) CF3CH3.
Нетрудно нарисовать структурные формулы этих соединений. Пример такой структурной формулы дан на рис. 1 (она соответствует соединению 12).
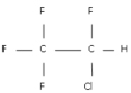
Рис. 1. Структурная формула соединения CF3CHClF из примера 1
В [13] приведены данные о наркотической активности этих соединений (степень активности характеризуется величиной lnAD50, где AD50 – это концентрация вещества, вызывающая наркоз у 50 % подопытных животных). В качестве графов, описывающих строение этих соединений, рассмотрим обычные структурные формулы этих соединений (рис. 1). Для построения МССС рассмотрим следующие фрагменты этих молекулярных графов: отдельные вершины (с учетом меток – C, H, Cl, F), цепочки длины один, два и три (при всех возможных вариантах расположения меток Cl, F, C, H на их вершинах); фрагменты, представляющие собой два изолированных ребра (при всех возможных вариантах расположения меток Cl, F, C, H на их вершинах). Общее число рассматриваемых подграфов равно 30. Рассмотрим все инварианты, равные числам вхождения этих подграфов в молекулярный граф. Далее используем метод 1 для построения корреляций «структура-свойство». Возьмем k = 5. Сначала были найдены 5 инвариантов g1-g5, которые дают наилучшую 5-параметрическую модель (с R = 0.982). Они соответствуют базовым фрагментам следующего вида: Cl, H?C?F, F?C?Cl, Cl?C?Cl, F?C?C?F.
Далее, были построены параметры вида gigj (i, j = 1,...,5). Из всех полученных параметров вида gi и gigj снова были выбраны пять параметров, дающих наилучшую линейную 5-параметрическую МССС. В результате было получено следующее нелинейное уравнение относительно 4 параметров g1-g4:
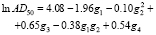
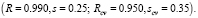
Эта МССС более точная, чем предыдущая. Отметим, что наилучшая однопараметрическая корреляция с инвариантами из набора g1-g5 имеет коэффициент корреляции R = 0.857.
Сравним эти результаты с аналогичными результатами, полученными для тех же самых данных другим методом и приведенными в [13]. В этой работе приведено однопараметрическое линейное корреляционное уравнение, в котором в качестве молекулярного дескриптора выступает некоторый квантово-химический параметр; соответствующий коэффициент корреляции R = 0.606. Таким образом, предлагаемый подход позволяет построить более точную МССС (если сравнивать их по коэффициенту корреляции) даже для случая одного параметра.
Пример 2. Рассмотрим следующее множество N = 14 соединений:
1) 2,3,5-тринитротолуол; 2) 2,4,5-тринитротолуол; 3) 1,3,5-тринитротолуол;
4) 2,3,6-тринитротолуол; 5) 2,4,6-тринитротолуол; 6) 3,4,5-тринитротолуол;
7) 2,3,4-тринитротолуол; 8) 2,5-динитротолуол; 9) 1,3-динитробензол;
10) 3,5-динитротолуол; 11) 2,4-динитротолуол; 12) 3,4-динитротолуол;
13) 2,3-динитротолуол; 14) 2,6-динитро- толуол.
В работе [13] приведены данные по мутагенной активности этих соединений (активность характеризуется величиной lnm (на Salmonella typhimurium), где m – число ревертантов на наномоль). Обозначим фрагменты H, NO2, CH3 структурных формул этих соединений буквами C, B, A; изобразим бензольное кольцо, являющееся основой всех этих соединений, простым шестичленным циклом. Тогда этим структурам можно поставить в соответствие однотипные взвешенные молекулярные графы, имеющие вид шестиугольника с метками вершин из множества A, B, C. Пример такого графа (для соединения 1) дан на рис. 2.
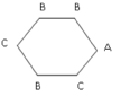
Рис. 2. Молекулярный граф соединения 1) в примере 2
Рассмотрим следующие базовые подграфы этих графов: 1) изолированные вершины с метками А, В, С; 2) цепочки длины один (т.е. ребра) следующего вида: В?В, В?С, С?С; 3) цепочки длины два следующего вида: С?С?С, В?С?С, В?С?В, В?В?С, С?В?С, В?В?В; 4) цепочки длины три следующего вида: В?В?С?С, В?В?С?В, С?В?В?С, В?В?В?С, С?С?С?В, В?С?С?В, С?В?С?С; 5) подграфы, состоящие из двух изолированных ребер: С?С / С?С, С?В / С?В, С?В / С?С, С?В / В?В, В?В / С?С.
Рассмотрим все инварианты, равные числам вхождения этих подграфов в молекулярный граф. Затем используем метод 1 для построения МССС, взяв k = 5. Были найдены 5 параметров g1-g5, которые дают наилучшую 5-параметрическую линейную МССС (R = 0.970, s = 0.648); эти параметры соответствуют следующим фрагментам: B, B?B/C?C, B?B?C, A, C. Затем на основе выбранных инвариантов g1-g5 были построены новые параметры вида gigj, (gigj)2 (i,j = 1,...,5). Из полученного множества параметров снова были отобраны 5 параметров, дающих наилучшую 5-параметрическую МССС. В итоге было получено следующее нелинейное уравнение (относительно g1-g5), являющееся более точным, чем предыдущее:
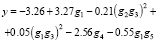
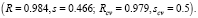
Сравним эти результаты с аналогичными результатами для тех же самых данных, полученных другими авторами, представленными в [13]. В [13] сообщается о линейной корреляции между lnm и энергией нижней свободной молекулярной орбитали (LUMO), которая находится квантово-химическими методами. Эта корреляция имеет R = 0.940. В нашем случае наилучшая однопараметрическая корреляция имеет R = 0.914, а для наилучшей двухпараметрической корреляции R = 0.940.
Пример 3. Рассмотрим следующее множество N = 17 хлорзамещенных анилинов с известными значениями токсичности logEC50-1 (EC50 – это концентрация вещества, измеряемая в миллимолях на литр, вызывающая уменьшение люминесценции морских бактерий (Photobacterium phosphoreum) в 2 раза в течение 30 минут [14]: анилин, пентахлораналин, m-хлоранилин (при m = 2,3,4), m,k-дихлоранилин (при m,k = 2,3; 2,4; 2,5; 2,6; 3,4; 3,5), m,n,k-трихлоранилин (при m,n,k = 2,3,4; 2,4,5; 2,4,6; 3,4,5), m,n,k,p-тетрахлоранилин (при m,n,k,p = 2,3,4,5; 2,3,5,6). Обозначим фрагменты NH2, Cl, H, структурных формул этих соединений буквами A, B, C; изобразим бензольное кольцо, являющееся основой всех этих соединений, простым шестичленным циклом. Тогда этим структурам можно поставить в соответствие однотипные взвешенные молекулярные графы, имеющие вид шестиугольника с метками вершин из множества A, B, C. Пример такого графа (для 3-хлоранилина) дан на рис. 3.
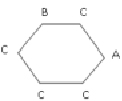
Рис. 3. Молекулярный граф 3-хлоранилина из примера 3
Рассмотрим следующие базовые подграфы этих графов: 1) изолированные вершины с меткой В; 2) цепочки длины один и два со всеми возможными расположениями меток A, B, C на их вершинах; 3) цепочки длины три со всеми возможными комбинациями меток B и C в их вершинах; 4) подграфы, состоящие из двух изолированных ребер со всеми возможными комбинациями меток B и C на их вершинах.
Рассмотрим все инварианты, равные числам вхождения этих подграфов в молекулярный граф. Затем используем метод 2 для построения МССС (рассматривая степени инвариантов только с целыми показателями и взяв k = 6). В соответствующей процедуре первоначально были выбраны 6 инвариантов g1-g6, которые дают наилучшую 6-параметрическую линейную МССС. Эти инварианты соответствуют следующим подграфам: C?C?C, C?B?C, B?B / B?B, C?B / B?B, B?B?B?C, B?B?B?B. Далее была получена следующая нелинейная МССС (относительно 6 параметров g1-g6):
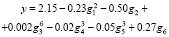
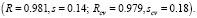
Отметим, что добавление к этому множеству 6 исходных параметров новых инвариантов вида gigj (i,j = 1,…,6) не позволяет увеличить точность МССС. Сравним этот результат с аналогичным результатом для тех же данных, полученным другими авторами в [14]. В этой работе для построения моделей был использован хорошо известный метод TLSER (Theoretical Linear Solvation Energy Relationship). Согласно этому подходу, рассматриваемое свойство есть линейная функция 6 молекулярных параметров; один из них – ван-дер–ваальсов молекулярный объем V, а другие 5 параметров – некоторые квантово-химические величины, найденные для данных соединений. В этой работе установлено, что из этих 6 параметров только один параметр квантово-химического типа является существенным, и для соответствующей корреляции R = 0.658, s = 0.45. Кроме того, если исключить из данного множества соединений «выпадающее» соединение 17), то коэффициент корреляции увеличится и станет равным R = 0.833. Однако в нашем подходе нет необходимости исключать какое-либо соединение из заданного множества, так как полученная МССС достаточно точна для полного множества соединений. Если мы тем не менее исключим это соединение из исходной выборки и построим новую МССС, то ее качество практически останется тем же: R = 0.981, s = 0.15. Отметим также, что наилучшая линейная однопараметрическая МССС, получаемая на основе нашего подхода, имеет R = 0.772, а 5-параметрическая МССС – R = 0.975.
Пример 4. Рассмотрим следующее множество 5-(диалкилвинил)-5-алкилбарбитуровых кислот, состоящее из N = 14 соединений (рис. 4; R1 – диалкилвинил, R2 – алкилвинил), для которых заместители R1 и R2 имеют следующий вид, соответственно [15]:
1) EtCH=C(Me)- , Me; 2) EtCH=C(Me)- , Et; 3) EtCH=C(Me)- , Pr; 4) EtCH=C(Me)- , i-Pr; 5) MeCH=C(Et)- , Et; 6) MeCH=C(Et)- , Et; 7) MeCH=C(Et)- , Pr; 8) MeCH=C(Et)- , i-Pr; 9) PrCH=C(Me)- , Me; 10) PrCH=C(Me)- , Et; 11) i-PrCH=C(Me)- , Me; 12) BuCH=C(Me)- , Me; 13) BuCH=C(Me)- , Et; 14) EtCH=C(Pr)- , Et.
Здесь использованы следующие обозначения: Me – это CH3-, Et – это CH3CH2-, Pr – это CH3CH2CH2-, i-Pr – это CH3CH(CH3)-, Bu – это CH3CH2CH2CH2-.
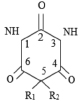
Рис. 4. Производные барбитуровой кислоты, рассматриваемые в примере 4
Для этих соединений известны значения их токсичности LD50 (мг/кг) при воздействии на белых мышей [15]. Построим по этим данным МССС при k = 5, используя предложенные выше методы. Сначала надо построить молекулярные графы этих соединений. Так как все соединения данного набора отличаются лишь заместителями R1 и R2, то построим графы этих соединений, состоящие только из двух изолированных подграфов, отвечающих R1 и R2. При этом атомы водорода учитывать не будем, а атомам углерода сопоставим вершины графа без меток, все химические связи изобразим с помощью однократных ребер (игнорируя двойные связи в R1). При этом атом углерода с номером 5 (рис. 4) будет учитываться в каждом из подграфов, соответствующих R1 и R2. В качестве примера такого молекулярного графа на рис. 5 приведен граф соединения 4). В нем левый фрагмент соответствует R1 (EtCH=C(Me)-), а правый – R2 (i-Pr), самая правая вершина в левом фрагменте и самая левая во втором соответствуют атому углерода с номером 5 на рис. 4.
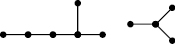
Рис. 5. Молекулярный граф соединения 4) в примере 4
Рассмотрим следующие 5 базовых подграфов этих графов, содержащих от двух до четырех вершин: цепочки длины 1, 2, 3; подграфы, состоящие из двух изолированных ребер; цепочки длины 3. Обозначим числа вхождения этих подграфов в граф через g1-g5 соответственно.
Используем для построения МССС сначала первый метод подбора аппроксимирующей функции F. На 1-м этапе строим линейную корреляцию с исходными параметрами g1-g5 следующего вида:
y = a1g1 + a2g2 + a3g3 + a4g4 + a5g5 +
+ a6 (R = 0.933, s = 66.65).
На 2-м этапе, используя степени исходных параметров, получаем более точную корреляцию вида:
y = b1g1 + b2(g3g4) + b3(g2g5) + b4g4 + b5g3 +
+ b6 (R = 0.948, s = 58.87).
На 3-м этапе, применяя еще раз первый подход к полученному новому набору параметров, улучшаем результат 2-го этапа, получая новую МССС вида:
y = c1g1 + c2(g3g4) + c3(g3g4)2 + c4(g1)2 +
+ c5(g2g5)2 + c6 (R = 0.954, s = 55.73).
Теперь построим МССС, используя второй способ подбора функции F. Получаем модель, более точную, чем последняя из описанных выше:
y = d1(g1)3/20 + d2(g3)1/4 + d3(g1)1/8 + d4(g2)3 +
+ d5(g3)1/8 + d6 (R = 0.968, s = 46.78).
В этих уравнениях a1-a6, b1-b6, c1-c6, d1-d6 – некоторые коэффициенты, определяемые методом наименьших квадратов. Однако к полученной модели (или к полученному набору параметров) можно применить первый метод построения аппроксимирующей функции. В этом случае получаем МССС с новым набором параметров (g1)3/20, (g1)1/8⋅(g3)1/8, (g1)1/8, (g3)1/4⋅(g2)3, (g3)1/4⋅(g1)1/8 (R = 0.969, s = 45,93), которая является более точной, чем предыдущая.
Отметим также, что при помощи описанных выше процедур можно получить МССС, имеющие примерно такую же точность, как и исходная, но с меньшим числом параметров. Например, в процессе построения модели на основе второго метода при 3 параметрах получаем коэффициент корреляции R = 0.937, в то время как для исходной модели с 5 параметрами R = 0.933.
Заключение
В настоящей статье предложен ряд общих подходов для построения нелинейных моделей связи «структура-свойство» для химических соединений. В этих подходах предполагается, что химические структуры представлены в виде меченых молекулярных графов. В качестве молекулярных дескрипторов в этих моделях используются числа вхождения в молекулярный граф специальных подграфов. Предложено обоснование выбора именно таких дескрипторов, основанное на некоторых результатах спектральной теории графов. Следует отметить, что достоинством молекулярных дескрипторов такого типа является то, что они вычисляются непосредственно по структуре молекулы и, кроме того, допускают структурную интерпретацию, в отличие, например, от топологических индексов сложной конструкции или дескрипторов, представляющих собой значения каких-либо физико-химических свойств.
В работе описаны две общие процедуры нахождения нелинейной аппроксимирующей функции в этих моделях; возможна также и комбинация этих процедур при построении модели. Получаемые модели базируются на некоторой исходной линейной регрессионной МССС, содержащей фиксированное число наилучших отобранных параметров. Предлагаемые методики, оперирующие с вышеуказанным набором параметров, позволяют получать более точные МССС, чем исходная, содержащие в точности такое же число параметров. Кроме того, можно строить и новые МССС примерно такой же точности, как и исходная линейная модель, но содержащие меньшее число параметров, что способствует расширению области применимости МССС.
Разработанные подходы имеют алгоритмический характер. Предлагаемые методы моделирования могут быть формально применены к любым базам данных по химическим соединениям и их свойствам, если эти соединения могут быть представлены графами, а свойства измеряются количественно. Применение предложенных методов продемонстрировано на ряде примеров, где в качестве «свойства» рассматриваются разные виды биологической активности. Из этих примеров следует, что предложенные подходы достаточно эффективны, и по крайней мере в рассмотренных случаях они превосходят некоторые другие подходы, основанные на определенных физико-химических теориях.
Следует также отметить, что результаты моделирования при помощи предложенных методов существенно зависят от способа представления молекулярных структур в виде графов.



