При решении широкого круга вычислительных задач в различных областях науки и техники возникает потребность численного решения уравнений одного или нескольких переменных, в частности при использовании неявных разностных схем для решения обыкновенных дифференциальных уравнений и уравнений в частных производных, интегральных и других, как правило, нелинейных уравнений. В настоящее время существует множество итерационных методов решения уравнений и их систем, однако использование традиционных итерационных методов решения нелинейных уравнений часто является малоэффективным из-за довольно большого количества итераций, что неминуемо приводит к значительному увеличению времени вычислений. Таким образом, очевидно, что вопрос о построении эффективных алгоритмов решения нелинейных уравнений остается актуальным в вычислительной математике и ее приложениях, в частности математическом моделировании, например при моделировании методом молекулярной динамики, где на каждом временном шаге необходимо решать от 103 до 107–1010 дифференциальных уравнений. В этом случае цена даже одной итерации при решении одного уравнения возрастает в миллионы раз [1]. Одним из эффективных итерационных методов решения нелинейных уравнений является метод Ньютона и различные его модификации? в том числе на основе непрерывного аналога метода Ньютона (НАМН). Эффективность метода Ньютона во многом основана на его высокой скорости сходимости. При численном решении эволюционного уравнения НАМН выбором подходящего значения шага численного интегрирования τ можно добиться сходимости метода при меньших ограничениях на значение начального приближения, чем в классическом методе Ньютона. Шаг интегрирования эволюционного уравнения τ может служить управляющим параметром для скорости сходимости итерационной схемы на основе НАМН. Предлагаемый в данной статье алгоритм выбора управляющего параметра τ позволяет сохранить высокую скорость сходимости даже в случае, когда значение производной в итерационной схеме метода Ньютона стремится к нулю. Данный алгоритм автоматически осуществляет выбор управляющего параметра в зависимости от значений невязки и производной левой части уравнения таким образом, чтобы окрестность выбора начального приближения обеспечивала устойчивую сходимость НАМН к точному решению.
В ходе работы предполагается провести исследование влияния шага численного интегрирования эволюционного уравнения НАМН на область и скорость сходимости метода и проанализировать алгоритмы выбора шага для численных методов решения нелинейных уравнений, использующие принцип уменьшения невязки. На основании проведённого анализа необходимо предложить эффективный алгоритм численного решения нелинейных уравнений.
Устойчивая итерационная схема НАМН
Итерационная схема приближенного решения нелинейного уравнения вида
f(x) = 0
на основе непрерывного аналога метода Ньютона может быть представлена в следующем виде [2]. Пусть на отрезке [a, b] существует единственный корень x*, функция f(x) дважды непрерывно дифференцируема и имеет нигде не обращающуюся в ноль первую производную 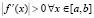 . Тогда для произвольного начального приближения x0∈[a, b] ∀ i = 1, 2, 3,… приближенное решение xi нелинейного уравнения f(x) = 0 может быть получено при помощи следующего рекуррентного соотношения:
. Тогда для произвольного начального приближения x0∈[a, b] ∀ i = 1, 2, 3,… приближенное решение xi нелинейного уравнения f(x) = 0 может быть получено при помощи следующего рекуррентного соотношения:
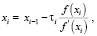
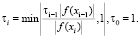 (1)
(1)
Здесь τi – шаг численного интегрирования эволюционного уравнения НАМН [3].
Согласно теореме о существовании решения нелинейного уравнения, установленной и доказанной Л.В. Канторовичем [4] при помощи метода Ньютона, для сходимости последовательности {xi} к точному решению x* при i → ∞ достаточно выполнение следующих условий: 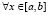 1)
1) 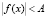 ; 2)
; 2) 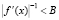 ; 3)
; 3) 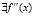 и
и 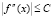 . Здесь A, B, C – действительные положительные константы.
. Здесь A, B, C – действительные положительные константы.
В случае если для некоторой итерации значение f′(xi) становится настолько малым, что итерационный процесс (1) становится расходящимся, для восстановления сходимости можно модифицировать итерационную схему (1) описанным ниже способом.
Пусть r > 0 – такое целое число, что выполнены следующие условия:
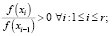
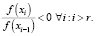
При этом точное решение удовлетворяет условию
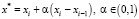
и
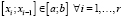 .
.
Тогда для нахождения i-того приближения вместо формулы (1) может быть использована следующая итерационная схема:
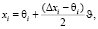 (2)
(2)
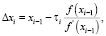
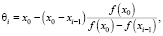
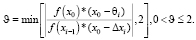
Алгоритм (2) может быть применён при следующих условиях:
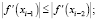
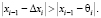
Величина θi является решением уравнения прямой, проходящей через точки f(x0) и f(xi–1). Алгоритм (2) может использоваться для управления величиной 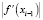 в случае возникновения расходимости итерационной схемы (1) при слишком быстром уменьшении абсолютной величины производной в окрестности корня уравнения [3]. Для вычисления величины τi при i ≤ r воспользуемся формулой
в случае возникновения расходимости итерационной схемы (1) при слишком быстром уменьшении абсолютной величины производной в окрестности корня уравнения [3]. Для вычисления величины τi при i ≤ r воспользуемся формулой
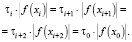
Тогда для величины τi можно получить следующую расчетную формулу:
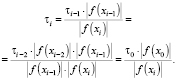 (3)
(3)
Если i > r, то 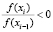 , тогда для того, чтобы не допустить расходимости метода (1) в результате возможного зацикливания при малых значениях производной вблизи корня, вместо схемы (1) предлагается использовать следующую итерационную схему:
, тогда для того, чтобы не допустить расходимости метода (1) в результате возможного зацикливания при малых значениях производной вблизи корня, вместо схемы (1) предлагается использовать следующую итерационную схему:
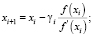
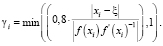 (4)
(4)
Для алгоритма (4) вводится дополнительный параметр ξ = xi–1, где xi–1 – значение итерационной переменной, в которой отношение невязок впервые становится отрицательным 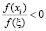 . Вместо параметра τi используется параметр γi, вычисляемый по формуле (4), который позволяет контролировать величину |ξ – xi+1|. Если величина |ξ – xi+1| становится равной нулю, то итерационный процесс (1) становится строго циклическим при том, что условие
. Вместо параметра τi используется параметр γi, вычисляемый по формуле (4), который позволяет контролировать величину |ξ – xi+1|. Если величина |ξ – xi+1| становится равной нулю, то итерационный процесс (1) становится строго циклическим при том, что условие 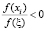 выполняется.
выполняется.
Действительно, в случае: 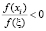 и
и 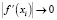 при i → ∞ может выполняться условие:
при i → ∞ может выполняться условие:
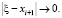
Тогда 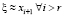 , откуда следует следующее приближенное равенство:
, откуда следует следующее приближенное равенство:
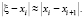
Данное неравенство позволяет сделать вывод о расходимости и полном зацикливании метода (1) в случае выполнения точного равенства 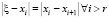 [5]. Чтобы избежать данного типа расходимости, используется итерационная схема (4), которая позволяет ∀i > r обеспечить выполнение следующего условия.
[5]. Чтобы избежать данного типа расходимости, используется итерационная схема (4), которая позволяет ∀i > r обеспечить выполнение следующего условия.
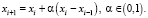
Данное условие приводит к строгому неравенству
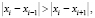 (5)
(5)
которое гарантирует устранение расходимости метода (1) в виде зацикливания. Подставив значение 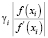 вместо
вместо 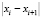 в неравенство (5), мы получим:
в неравенство (5), мы получим:
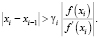 (6)
(6)
Это приводит к оценке для γi:
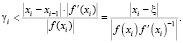 (7)
(7)
Схема алгоритма (2)–(4) представлена ниже.
Алгоритм решения нелинейного уравнения f(x) = 0
|
Input: |
eps – значение невязки, при достижении которого итерационный процесс останавливается. |
|
Output: |
N – количество выполненных итераций. θi – точка пересечения прямой, проходящей через точки x0, xi, c осью абсцисс. ξ – точка, для которой выполнилось условие ϑ – регулирующий коэффициент для xi . |
|
Initial data: |
x0 – начальное приближение. τ0 – начальное значение шага численного интегрирования эволюционного уравнения НАМН. |
while 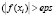 and
and 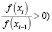 do
do
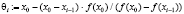
xi:= 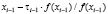
τi := 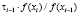
if τi > 1 then
τi ? 1
end if
if (f′(xi) < f′(xi–1) and ?xi–1 – xi?>?xi–1 – θi?) then
ϑ:=?f(x0)*(x0 – θi)/f(xi–1) ? (x0 – xi)?
if ϑ > 2 then
ϑ: = 2
end if
xi:= 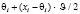
end if
end while
while 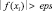 do
do
if 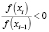 then
then
ξ:= xi–1
end if
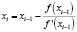
if 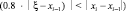 then
then
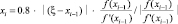
end if
end while
Входными данными для этого алгоритма является eps – точность нахождения приближенного решения xi Для уравнения f(x) = 0. Итерации заканчиваются при условии |f(xi)| ≤ eps. При этом выходным значением переменной N будет значение i, при котором впервые выполняется условие |f(xi)| ≤ eps. Начальными данными для алгоритма являются начальное приближение x0 и начальное значение шага численного интегрирования эволюционного уравнения НАМН τ0. Первый цикл с предусловием выполняется до тех пор, пока отношение невязок для соседних итераций положительно. После того, как упомянутое выше отношение невязок становится отрицательным 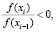 начинается выполнение второго цикла с предусловием. При этом определяется новая переменная ξ = xi–1 и вычисления проводятся в соответствии с алгоритмом (4). Значение 0,8, используемое для вычисления очередной величины xi, получено в результате вычислительных экспериментов с целью определения наиболее эффективного значения коэффициента в выражении для вычисления γi (4). Данное значение является оптимальным для увеличения области сходимости для различных значений начального приближения x0 и, соответственно, уменьшения количества итераций для нахождения приближенного решения заданной точности.
начинается выполнение второго цикла с предусловием. При этом определяется новая переменная ξ = xi–1 и вычисления проводятся в соответствии с алгоритмом (4). Значение 0,8, используемое для вычисления очередной величины xi, получено в результате вычислительных экспериментов с целью определения наиболее эффективного значения коэффициента в выражении для вычисления γi (4). Данное значение является оптимальным для увеличения области сходимости для различных значений начального приближения x0 и, соответственно, уменьшения количества итераций для нахождения приближенного решения заданной точности.
Алгоритм реализован на языке C++.
Численное исследование устойчивости алгоритма (2)–(4)
В табл. 1, 2 представлены результаты приближенного решения тестового уравнения f(x) = ln(x)sin3x-1,2 – 0,7 = 0 с использованием численного метода (2), (4). x* = 3,36985651 является точным решением тестового уравнения. В окрестности корня в точке x = 3,825049 производная f′(x) обращается в ноль, что может привести при неудачном выборе начального приближения x0 к зацикливанию стандартного НАМН.
Таблица 1
Зависимость количества итераций N от выбора начального значения x0 при фиксированном τ0 = 0,1
|
x0 |
|f(xN )| |
N |
|
2,5 |
1*10-6 |
8 |
|
3 |
1*10-4 |
3 |
|
3,2 |
1*10-10 |
3 |
|
3,3 |
1*10-5 |
4 |
Таблица 2
Зависимость количества итераций N от выбора начального значения τ0 при фиксированном x0 = 2,5
|
τ0 |
|f(xN )| |
N |
|
0,1 |
1*10-6 |
8 |
|
0,2 |
1*10-4 |
7 |
|
0,4 |
1*10-10 |
6 |
|
0,7 |
1*10-5 |
4 |
Анализ данных из табл. 1, 2 позволяет сделать следующие выводы. Как видно из табл. 1, чем ближе к корню выбирается начальное приближение x0, тем меньше итераций N необходимо для получения заданной точности приближенного решения тестового уравнения при помощи метода (2), (4). Данное свойство присуще всем методам ньютоновского типа. Данные табл. 2 демонстрируют возможность уменьшения количества итераций при фиксированном начальном приближении с помощью предложенного в статье метода (2), (4) за счет адекватного выбора начального значения шага численного интегрирования эволюционного уравнения НАМН τ0. При этом предложенная в статье модификация НАМН позволяет не допустить расходимости численного метода даже в случае зацикливания, если в окрестности корня, в некоторой точке, производная f’(x) обращается в ноль.
Заключение
В статье предложен новый подход к построению устойчивых численных схем на основе НАМН. Данный подход при помощи описанной в статье процедуры выбора шага численного интегрирования эволюционного уравнения НАМН не позволяет зацикливаться итерационному процессу численного решения уравнения f(x) = 0 в случае, если в окрестности корня уравнения производная f’(x) обращается в ноль. Тестовые расчеты для модельной задачи показали высокую эффективность предложенного авторами подхода для повышения устойчивости численных методов решения нелинейных уравнений на основе НАМН.




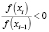 .
.