Моделирование пешеходных потоков является актуальной темой для исслледования, так как нашло большое количество приложений в различных областях науки в последние десятилетия. Особое значение понимание законов, которым подчиняется движение большой группы людей, имеет при моделировании эвакуационных сценариев, а также для организации движения по улично-дорожной сети.
Математические модели способны описывать динамику потока на различных уровнях: микроскопическом, мезоскопическом и макроскопическом. Микроскопические модели учитывают поведение в потоке каждого отдельного человека. Здесь можно выделить модель социальных сил и модель клеточных автоматов [1; 2]. На макроскопическом уровне предлагалось описывать потоки с помощью газодинамической и кинетической модели [3]. Существуют компьютерные программы, использующие оба типа моделей, позволяюшие решать локальные и глобальные задачи, обмениваясь результатами и данными внутри программы [2; 4; 5]. Проблема в том, что исходные данные для моделей разных уровней совершенно различны. Это вносит значительные трудности, так как сбор большого количества исходных данных сам по себе является трудной задачей.
Для отдельного класса задач требуется моделирование потока на некотором «среднем» уровне, когда отдельные участники движения учитываются с целью формирования параметров общего потока. Такие модели получили название мезоскопических.
Актуальной задачей является разработка математической модели, позволяющей определять параметры плотных пешеходных потоков для управления ими в режиме реального времени.
Целью данной работы является разработка мезоскопической модели плотного пешеходного потока, позволяющей при минимальном количестве исходных данных предсказывать параметры данного потока при эвакуационных сценариях.
Материал и методы исследования
При моделировании пешеходных потоков авторами зачастую за основу берутся аналогичные модели транспортных потоков. Не для всех типов решаемых задач это приемлемо, так как поток людей менее организован и подвержен влиянию большего количества случайных факторов. Согласно выводам, сделанным исследователями, существует эффект самоорганизации толпы, происходящий без внешнего воздействия по прошествии некоторого времени [2; 4]. В данной работе мы ставим цель описания сформировавшегося при эвакуации плотного потока, движущегося в определенном направлении к выходу. В этом случае мы можем взять за основу методы и приемы, использованные автором данной статьи при разработке модели транспортных потоков TIMeR_Mod [6].
Результаты исследования и их обсуждение
Гипотезу о нормальном распределении плотного пешеходного потока, движущегося в определенном направлении, доказывали экспериментально многие исследователи. Однако при описании потока пешеходов как случайного потока событий нормальный закон распределения применять затруднительно. Закон Эрланга при значениях параметра k ≥ 5 близок к нормальному и соответствует плотным потокам событий [7]. Поэтому при эвакуации из мест массового скопления людей по узким коридорам поток пешеходов будем аппроксимировать законом Эрланга (как и транспортный).
Плотность распределения специального закона Эрланга (или просто «закон Эрланга») имеет вид [7]:
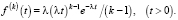(1)
Функция распределения Эрланга k-го порядка имеет вид:
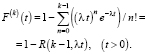(2)
Математическое ожидание M(T) и дис- персия D(T) в этом случае равны соответ- ственно:
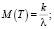
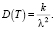(3)
1. Представление пешеходного потока как потока Пальма
Будем использовать теорию восстановления при моделировании пешеходного потока как случайного потока событий – потока Пальма. Предполагаем, что поток уже сформировался и движется в определенном направлении. Случайным событием считаем прибытие пешехода в точку пространства с фиксированной координатой по оси направления движения. Интервал между случайными событиями – это интервал по времени между последовательными прибытиями к фиксированной точке пространства двух подряд идущих пешеходов в потоке. Рассмотрим функцию восстановления H(t) = M(Nt) – математическое ожидание числа событий, произошедших за время t в случае (специального) распределения Эрланга. Изображение функции распределения временных интервалов в случае распределения Эрланга [8]:
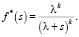(4)
А преобразование Лапласа для этой функции имеет вид:
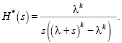(5)
Функцию H*(s) можно разложить на простые дроби, содержащие члены:
1) от полюса s = 0;
2) от ненулевых полюсов в точках, являющихся корнями уравнения f*(s) = 1.
Найдем корни этого уравнения:
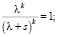
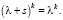(6)
Ненулевые корни имеют вид (здесь i – мнимая единица):
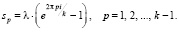(7)
Каждому простому ненулевому корню sp в разложении H*(s) соответствует дробь:
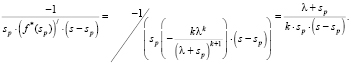(8)
То есть
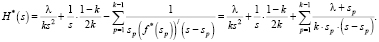(9)
Отсюда по таблицам находим оригинал, т.е. функцию восстановления H(t) – число событий, произошедших в течение интервала времени (0; t). Известно из теории операционного исчисления, что каждой дроби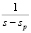 
соответствует оригинал 
.
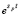В случае плотных пешеходных потоков, согласно исследованиям, закон распределения близок к нормальному, и его можно аппроксимировать (специальным) законом Эрланга порядка не ниже пятого.
Для получения точного аналитического задания функции восстановления рассмотрим k = 6.
Корни уравнения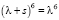 
в этом случае следующие:
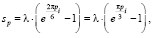
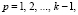(10)
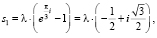
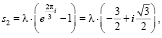
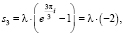
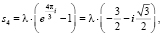
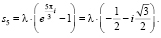
Изображение функции восстановления при k = 6 имеет вид:
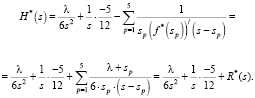(11)
Выразим R*(s):
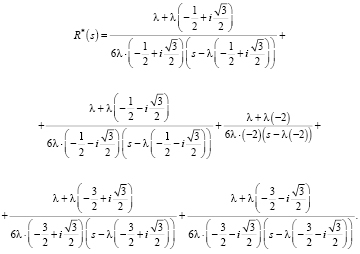(12)
После упрощения выражения и приведения его к виду, удобному для определения оригинала, получим следующее:
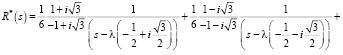
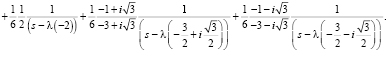(13)
Найдем оригинал по его изображению:
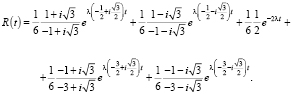(14)
Тогда получим:
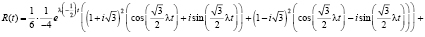
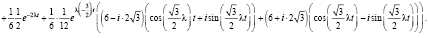
После упрощения выражения и приведения подобных слагаемых R(t) приобретает следующий вид:
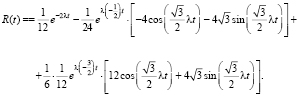(15)
Тогда функция восстановления при k = 6 следующая:
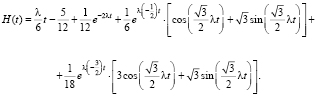(16)
Формула (16) задает функцию H(t), равную количеству пешеходов потока, прибывших к фиксированной точке за время t секунд. При эвакуационных сценариях H(t) численно равна количеству людей, подошедщих к перекрытому эвакуационному выходу за t секунд. При моделировании улично-дорожного движения H(t) определяет количество пешеходов, подошедших к пешеходному переходу за время горения запрещающего сигнала светофора [9].
2. Слияние нескольких пешеходных потоков перед перекрытым выходом
Рассмотрим теперь случай, когда перед эвакуационным выходом сливаются s пешеходных потоков. Согласно теории восстановления [7] для среднего числа восстановлений в интервале (0; t) в объединенном процессе справедливо соотношение:
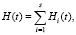(17)
где s – количество объединяемых процессов, Hi(t) – функция восстановления каждого из них.
То есть если в некоторой точке плоскости сливаются s пешеходных потоков, то количество пешеходов, пересекающих эту точку в промежуток (0; t) рассчитывается следующим образом:
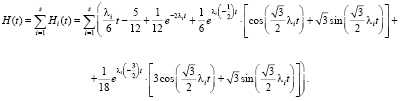(18)
Здесь λi – параметр Эрланга для i-го объединяемого потока.
3. Определение параметров распределения Эрланга по экспериментальным данным
С помощью видеодетекторов фиксируем величины интервалов Ti по времени (в секундах) между двумя последовательными прохождениями пешеходов в потоке точки с фиксированной координатой. Рассчитываем выборочную среднюю случайной величины T:
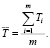(19)
Значение параметра k = 6, тогда параметр λ распределения Эрланга следующий:
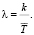(20)
Заключение
При планировании эвакуационных сценариев либо при управлении потоками пешеходов при чрезвычайном происшествии в режиме реального времени необходимо определять загруженность эвакуационных выходов. Имитационное моделирование с помощью макромоделей в данном случае неприменимо, так как требует больших затрат по времени и огромного количества исходных данных. Предлагаемый в работе аналитический метод позволяет при минимальном числе исходных данных в режиме онлайн мгновенно предсказывать загруженность, а следовательно, выбирать оптимальный способ перенаправления пешеходных потоков при эвакуации.