Многие колебательные процессы описываются нелинейными дифференциальными уравнениями в частных производных гиперболического типа. Поэтому задачи оптимального управления такими процессами всегда являются актуальными. В данной работе исследуется задача оптимального управления колебательной системой, описывающейся квазилинейным уравнением в частных производных гиперболического типа. Строится приближенное оптимальное управление. Доказана сходимость приближения по функционалу.
Цель исследования: исследовать задачу оптимального управления слабо управляемой квазилинейной системой с распределенными параметрами. Исследование состоит в том, чтобы построить приближенное оптимальное управление, доказать сходимость приближения по функционалу, получить оценки сколь угодной точности.
Рассмотрим задачу оптимального управления слабо управляемой квазилинейной системой с распределенными пара- метрами.
Пусть управляемый процесс описывается в области
Q = {0 < x < 1, 0 < t < T}
уравнением
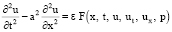(1)
с начальными
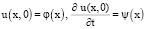(2)
и граничными
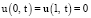(3)
условиями.
Здесь U(x, t) – функция, которая описывает рассматриваемый колебательный процесс, a – некоторая известная скалярная величина; ε – положительный малый параметр; F – некоторая непрерывная функция своих аргументов, определенная в области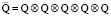 
, где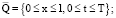 
p(x, t) – управляющая функция из некоторого класса допустимых управлений.
Следуя [1; 2], обозначим через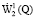 
замыкание в норме 
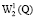множества всех непрерывно дифференцируемых в Q функций, равных нулю вблизи границы множества Q, а через 
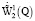– элементы из 
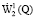, равные нулю при t = T.
Обобщенным решением смешанной задачи (1)–(3) называется [3–5] такая функция u(x, t), которая принадлежит пространству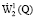 
и удовлетворяет интегральному тождеству
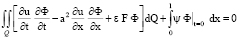(4)
для любой функции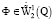 
. При этом первое условие (2) понимается в том смысле, что
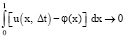при Δt → 0. (5)
Теперь сформулируем задачу оптимального управления: найти допустимое управление p0(x, t) и соответствующее ему обобщенное решение u(x, t) смешанной задачи (1)–(3), на которых функционал
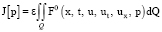(6)
принимает наименьшее возможное значение.
Будем предполагать в (1), (2), (6), что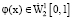 
, 
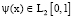и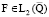 
. Также предположим, что функции F(x, t, u, ut, ux, p) и F0(x, t, u, ut, ux, p), входящие в правую часть уравнения (1) и в функционал (6), удовлетворяют условиям [6].
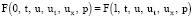
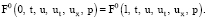(7)
Рассмотрим невозмущенное уравнение
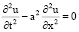(8)
при тех же начальных и граничных условиях (2), (3).
Известно, что при вышеприведенных предположениях существует счетная система положительных собственных чисел {λk} (k = 1, 2, …) и соответствующая ей полная ортонормированная система обобщенных собственных функций {Хk(х)}, а единственное обобщенное решение смешанной задачи (8), (2), (3) можно представить в виде ряда
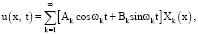(9)
где ωk = а λk – частоты нормальных колебаний,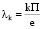 
,
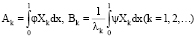. Так как система обобщенных собственных функций {Хk(х)} полна в L2[0, 1] и 
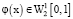для любых функций 
и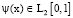 
их ряды Фурье по этой системе сходятся в 
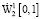и L2[0, 1] соответственно к самим функциям.
В связи с малостью возмущений форма колебаний возмущенной системы определяется с достаточной точностью теми же обобщенными собственными функциями Хk(х), что и форма колебаний невозмущенной системы.
Решение возмущенного уравнения (1) ищем в виде ряда [7; 8]
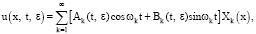(10)
где Ak(t, ε), Bk(t, ε), (k = 1, 2,…) – неизвестные функции, подлежащие определению; Хk(х), (k = 1, 2,…) – обобщенные собственные функции краевой задачи.
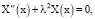
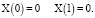
Предположим, что [9–11]
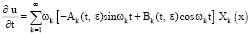
и функция
,
,
, 
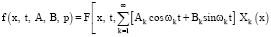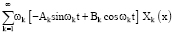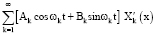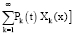(11)
разлагается в ряд Фурье по обобщенным собственным функциям
Хk(х) (k 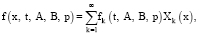= 1, 2,…):
(12)
где fk(t, A, B, p) – коэффициент Фурье.
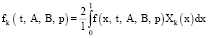. (13)
Тогда для определения неизвестных функций Ak(t, ε) и Bk(t, ε) получим счетную систему обыкновенных дифференциальных уравнений
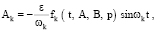
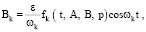(14)
k = 1, 2, … .
Как было отмечено выше, функции φ(x) и ψ(x) разлагаются в ряд Фурье по обобщенным собственным функциям Хk(х)
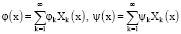(15)
с коэффициентами Фурье
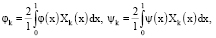(16)
и эти ряды (15) сходятся к самим функциям φ(x) и ψ(x) соответственно.
Отсюда для однозначного определения неизвестных функций Ak(t, ε) и Bk(t, ε) в (14) будем иметь начальные условия
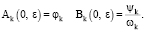(17)
При аналогичном разложении в ряд Фурье подынтегральной функции F0 по обобщенным собственным функциям Хk(х) функционал (6), оценивающий качество управления исходным колебательным процессом, преобразуется к виду
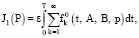(18)
где
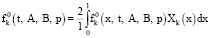(19)
коэффициенты Фурье разложения в ряд функции
,
,
, 
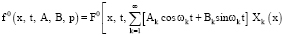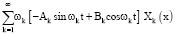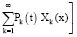
по обобщенным функциям Хk(х).
Вместо счетной системы обыкновенных дифференциальных уравнений (14) рассмотрим укороченную систему
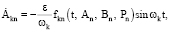
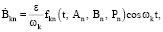(20)
k = 1, 2, … n.
с начальными условиями
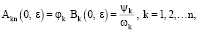(21)
где
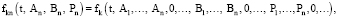
а вместо функционала (18) рассмотрим функционал
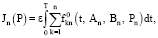(22)
где
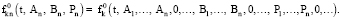
Рассмотрим функцию
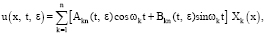(23)
где Akn(t, ε), Bkn(t, ε) есть решение системы (20) начальным условием (21) при каждом фиксированном Р. Определенную таким образом функцию u(x, t, ε) назовем приближенным обобщенным решением смешанной задачи (1)–(3).
Теперь вместо сформулированной выше задачи оптимального управления (1)–(3), (6) будем решать другую задачу оптимального управления, т.е. будем искать управляющую функцию Р на класс допустимых управлений, которая вместе с решениями системы
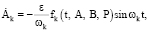
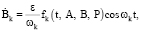(24)
k = 1, 2, … n
с начальными условиями
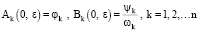(25)
минимизирует функционал
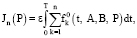(26)
где A = {A1, ….., An}, B = {B1, ….., Bn}, P = {P1, ….., Pn}.
Согласно необходимому условию оптимальности в форме принципа максимума Понтрягина [5; 10; 14] составим функцию Гамильтона Н
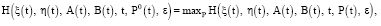(27)
где Н имеет вид
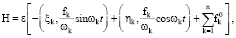(28)
где ξk(t), ηk(t), (k = 1, 2,…, n) – сопряженные функции и функциям Ak(t) и Bk(t) соответственно, которые удовлетворяют отношениям
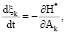
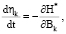(29)
где
,
,
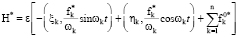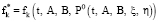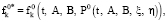(30)
а оптимальное управление
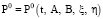
определяется из (27).
Предполагая, что функции f* и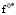 
обладают необходимыми свойствами гладкости, окончательно имеем каноническую систему уравнений краевой задачи принципа максимума
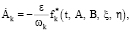
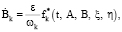
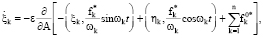
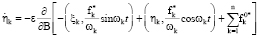(32)
с начальными
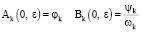
и краевыми
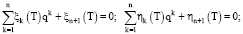(33)
условиями, получаемыми из условия трансверсальности [5; 6].
Здесь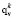 
– постоянный вектор, который исключается при решении краевой задачи (32), (25), (33).
Пусть теперь P0 есть оптимальное управление для задачи (24)–(26), а Р* есть оптимальное управление для задачи (14), (17), (18). Также предположим, что коэффициенты Фурье (19) удовлетворяют условию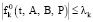 
(k = 1, 2,…), где λk образуют сходящийся числовой ряд 
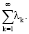Тогда, очевидно, имеет место неравенство
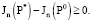
Отсюда согласно неравенству (1.10) в [12] имеем
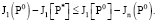(34)
Оценим правую часть неравенства (34)
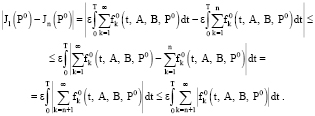
Согласно сделанному выше предположению получим
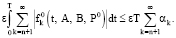
По признаку сходимости числового ряда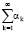 
имеем
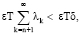
где δ > 0 малая const. Отсюда окончательно получим оценку
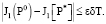
Теперь находим предел при n → ∞
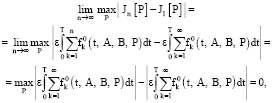
т.е.
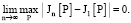
Тогда на основании теоремы 2 в [12–14] имеем сходимость
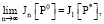
что и требовалось доказать.
Заключение
С помощью асимптотического разложения исходная краевая задача оптимального управления приведена к счетной системе обыкновенных дифференциальных уравнений. Для приближенного оптимального управления выписана каноническая система уравнений краевой задачи принципа максимума. Доказана сходимость приближения по функционалу и получены некоторые оценки.