Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

Современная экономическая конъюнктура создает сложные условия функционирования для хозяйствующих субъектов. Это обусловлено колебаниями потребительского спроса, постоянно усиливающейся конкуренцией и научно-техническим прогрессом. Отдельным хозяйствующим субъектам для успешного развития зачастую не хватает различных видов ресурсов. В этой связи возникает необходимость объединения усилий с другими предприятиями и организациями для достижения синергетического эффекта и реализации общих целей. Существует множество форм интеграции хозяйствующих субъектов. В настоящее время особое внимание уделяется кластерной форме интеграции предприятий. Каждое предприятие кластер сохраняет свою имущественную независимость, а интеграция заключается в объединении ресурсов и знаний для реализации совместных проектов по развитию территории. Кремниевая Долина, автомобильный кластер Восточной Германии, французская Косметическая Долина и другие аналогичные интегрированные структуры давно зарекомендовали себя как лидеры в производстве инновационной продукции и примеры для подражания по части территориального сотрудничества.

Многие авторы посвящали свои исследования вопросам формирования и развития интегрированных производственных систем. Отдельные труды [1–3] использовались при проведении настоящего исследования. Значительно реже встречаются работы, посвященные разработке оптимизационных решений по развитию интегрированных структур. В процессе разработки управленческих решений целесообразно обращаться к математическим методам, с помощью которых можно выявить внутрисистемные зависимости. Готовые методики оптимизационного моделирования параметров производственных систем будут способствовать разработке стратегических и тактических планов и прогнозов. На решение данной проблемы направлено исследование авторов.

Целью представленного в статье исследования является разработка комплексной методики оптимизационного моделирования параметров ресурсоэффективности территориально-производственных систем. Разработанная методика должна способствовать разработке управленческих решений по развитию предприятий, входящих в исследуемую систему. Учитывая, что интегрированные структуры по своим производственным и экономическим параметрам существенно различаются в зависимости от масштабов деятельности и отраслевой принадлежности, следует в качестве критерия обозначить гибкость методики, подразумевающую вариативность результирующих показателей и их детерминант.

Материалы и методы исследования

Математическое моделирование и оптимизация параметров функционирования территориальных производственных систем является сложной методологической проблемой, которая освещается в научных трудах различных авторов. В частности, проводимое авторами исследование опирается на следующие работы [4–6].

Первым вопросом исследования является определение целевого показателя, определяющего эффективность функционирования территориально-производственной системы. В современных реалиях в поисках путей развития хозяйствующих субъектов во главу угла зачастую ставится ресурсосбережение. В частности, об этом свидетельствует паспорт Национального проекта «Производительность труда и поддержка занятости» [7], в рамках которого программы ресурсосбережения отечественных предприятий позиционируются в качестве приоритета государственной поддержки.

Математические методы моделирования требуют наличия конкретных параметров и показателей, поэтому результативность ресурсосбережения необходимо формализовывать. Предприятия и производственные системы, которые они образуют, потребляют различные виды ресурсов, в числе которых трудовые, материально-технические, финансовые, нематериальные и другие. В результате использования ресурсов предприятия производят продукцию, работы, услуги. Ввиду возможной широты ассортимента наиболее удобным для расчетов количественным выражением выпуска является денежное. Однако выручка от реализации продукции, работ, услуг не характеризует эффективность использования ресурсов, поскольку не учитывает их затрачиваемые объемы. В этой связи в качестве денежного выражения ресурсоэффективности производственной системы более корректно использовать сумму прибыли, поскольку именно данный показатель отражает разницу объема вырученных в результате использования ресурсов средств и издержек на их приобретение и использование.

Таким образом, в качестве суммарного показателя ресурсоэффективности производственной системы рассматривается суммарная годовая прибыль до налогообложения предприятий, образующих данную систему. Данный показатель предлагается рассчитывать по формуле

РЭ = 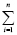Пднi , (1)

где РЭ – ресурсоэффективность исследуемой производственной системы в денежном выражении; Пднi – годовая прибыль до налогообложения i-го предприятия исследуемой производственной системы; n – количество предприятий в исследуемой производственной системе.

Прибыль предприятия является результирующим показателем, который зависит от огромного количества факторов. Поиск количественно измеримых параметров функционирования предприятия является следующим шагом в рамках предложенной методики. Поскольку исследование фокусируется на вопросах ресурсосбережения, то на наличие математических зависимостей следует исследовать количественные измерители различных ресурсов предприятия. Можно использовать абсолютные показатели, такие как численность персонала, суммарная стоимость определенных видов ресурсов, объемы затрат на НИОКР и другие. Однако более устойчивые модели получаются с применением относительных показателей, к которым можно отнести долю затрат на НИОКР в себестоимости продукции, соотношение управляющих кадров и исполнителей, доли определенных видов имущества в сумме активов предприятия и т.п.

После подготовки необходимых данных предполагается следующий алгоритм действий:

1. Расчет суммарной ресурсоэффективности производственной системы за определенный период времени. Следует понимать, что в целях повышения качества статистической модели необходимо максимизировать число наблюдений. В качестве единицы наблюдения может быть использована годовая суммарная прибыль или квартальная. Аналогичным образом следует подготовить значения предполагаемых детерминант прибыли. Далее методом корреляционно-регрессионного анализа определяются факторы ресурсоэффективности и разрабатывается регрессионная модель ресурсоэффективности исследуемой производственной системы.

2. Подготовка задачи математического программирования на максимизацию ресурсоэффективности. В качестве целевой модели используется ранее подготовленная регрессионная модель ресурсоэффективности. Возникает задача подготовки системы ограничений. Для этого необходимо опять обратиться к методу корреляционно-регрессионного анализа. Естественными ограничителями эффективности производственной системы являются ее экстенсивные и интенсивные возможности. Предприятие не может позволить себе нанимать персонал сверх необходимой нормы, не может вкладывать неограниченные объемы денежных средств в основные и оборотные фонды. Данные количественные ограничения определяют экстенсивные возможности предприятия. В то же время в определенные периоды предприятия характеризуются определенным лимитом результативности использования ресурсов. Другими словами, предприятия не могут демонстрировать сколь угодно высокую фондоотдачу, рентабельность или выработку. Под этим следует понимать интенсивные возможности. Обозначенные показатели имеют количественное ограничение, что может быть использовано в системе ограничений задачи математического программирования. Для этого необходимо выявить статистические зависимости между показателями-ограничениями и факторами ресурсоэффективности и построить соответствующие регрессионные модели.

3. Обозначенные выше показатели-ограничения могут сильно отличаться в различные периоды функционирования производственной системы. Эти различия позволили предложить типологию уровней развития производственной системы. В этой связи предлагается находить не одно решение задачи математического программирования, а несколько, в зависимости от количества типов.

4. Полученные решения задачи математического программирования на максимизацию ресурсоэффективности анализируются и интерпретируются в виде оптимальных параметров производственной системы, на достижение которых должны быть направлены управленческие решения.

Как было обозначено выше, показатели-ограничения будут варьироваться от уровня развития производственной системы, в связи с чем предложена типология, представленная в табл. 1.

Предложенную методику предлагается апробировать на примере территориальной производственной системы г. Нижнекамска. Объектами исследования являются крупнейшие производственные предприятия города, к которым относятся ПАО «Нижнекамскнефтехим», ПАО «Нижнекамскшина», АО «ТАИФ-НК» и АО «ТАНЕКО». В первую очередь данные предприятия как производственную систему характеризует единство в рамках технологической цепочки. В частности, ПАО «Нижнекамскнефтехим» использует сырье (прямогонный бензин, ШФЛУ), поставляемое АО «ТАИФ-НК» и АО «ТАНЕКО», для производства широкого ассортимента нефтехимической продукции. В свою очередь, ПАО «Нижнекамскнефтехим» поставляет синтетический каучук для производства шин на ПАО «Нижнекамскшина». Более того, данные предприятия являются ядром производственной сферы всего города, что позволяет при взаимодействии с ними развиваться другим хозяйствующим субъектам.

Результаты исследования и их обсуждение

Согласно изложенному алгоритму в первую очередь была разработана регрессионная модель ресурсоэффективности территориальной производственной системы г. Нижнекамска. Для этого были использованы статистические данные по исследуемым предприятиям за 2010–2019 гг. Анализ выявил сильную связь между суммарной прибылью предприятий и относительной долей отдельных видов оборотных активов в их общей сумме. Разработанная регрессионная модель имеет вид формулы

РЭ = 457*Х1 + 416*Х2 – 52, (2)

где Х1 – средняя доля производственных запасов на балансе исследуемых предприятий;

Х2 – средняя доля денежных средств на балансе исследуемых предприятий.

Для внесения большей ясности следует раскрыть формулы расчета выявленных факторов ресурсоэффективности. Показатель x1 рассчитывается по формуле

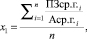(3)

где ПЗср.г.i – среднегодовая стоимость производственных запасов i-го предприятия территориальной производственной системы; Аср.г.i – среднегодовая стоимость всех производственных активов i-го предприятия территориальной производственной системы; n – количество анализируемых предприятий территориальной производственной системы.

Аналогичным образом представим показатель x2 в рамках формулы

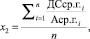(4)

где ПЗср.г.i – среднегодовая стоимость денежных средств на балансе i-го предприятия территориальной производственной системы; Аср.г.i – среднегодовая стоимость всех производственных активов i-го предприятия территориальной производственной системы; n – количество анализируемых предприятий территориальной производственной системы.

Далее были разработаны регрессионные модели показателей-ограничений для территориально-производственной системы города Нижнекамска. В результате была построена задача линейного программирования на максимизацию ресурсоэффективности, имеющая вид формулы

РЭ = 457*x1 + 416*x2 – 52,

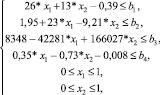(5)

где b1 – среднее значение фондоотдачи предприятия территориально-производственной системы г. Нижнекамска; b2 – среднее значение коэффициента оборачиваемости оборотных активов территориально-производственной системы г. Нижнекамска; b3 – среднее значение выработки на одного работника территориально-производственной системы г. Нижнекамска; b4 – среднее значение коэффициента рентабельности активов территориально-производственной системы г. Нижнекамска.

Представленная задача была решена в трех вариациях значений показателей-ограничений согласно трем уровням развития территориальной производственной системы, представленным в табл. 1. Решения и значения параметров представлены в табл. 2.

Полученные результаты свидетельствуют о том, что по мере повышения уровня развития системы нижнекамским предприятиям целесообразно наращивать долю производственных запасов и денежных средств в структуре производственного имущества. Данные указывают на то, что консервативная стратегия управления текущими активами является оптимальной для исследуемой территориально-производственной системы. Другими словами, по мере улучшения ситуации на сбытовых рынках и повышения эффективности производственной системы предприятиям следует увеличивать оборотный капитал, чтобы обеспечивать бесперебойные поставки продукции, тем самым максимизируя ресурсоэффективность. Представленные в табл. 2 значения долей производственных запасов и денежных средств могут быть рекомендованы предприятиям территориально-производственной системы г. Нижнекамска в качестве нормативных.

Заключение

Разработанная методика адекватна поставленной цели, что подтверждают результаты апробации. Полученные значения параметров территориально-производственной системы позволили определить оптимальную стратегию управления текущими активами, направленную на максимизацию уровня ресурсоэффективности. Следует отметить определенную гибкость методики, поскольку в рамках предложенных алгоритмов может быть проанализирован и спрогнозирован широкий ряд производственно-экономических параметров для существенного числа предприятий, объединенных в рамках единой территориально-производственной системы.

Исследование выполнено в рамках гранта Президента РФ по государственной поддержке ведущих научных школ РФ № НШ-2600.2020.6.