Большинство современных информационных систем, приложений, рекомендательных систем используют деревья решений в тех случаях, когда необходимо отнести объект к определенному классу из некоторого их числа, которые при этом не пересекаются. Если рассматриваемая переменная является дискретной, то полученное дерево называют классификационным, а если непрерывной, то дерево будет регрессионным. Широко известными примерами применения деревьев регрессий и классификационных деревьев можно назвать устройства и системы распознавания речи, текста, изображений (в том числе и анализ изображений или даже видео), жестов, алгоритмы и инструменты когнитивного поиска, системы обнаружения спама в веб-приложениях или соцсетях.
Параметры алгоритмов в машинном обучении настраиваются автоматически на основе некоторой обучающей выборки, а иными словами, некоторого множества объектов с известными атрибутами, характеристиками или соответствующими им ответами. Качество прогнозов и решения поставленной перед алгоритмами задачи напрямую зависит от качества обучения на начальной выборке.
В контексте рассматриваемых классификационных моделей алгоритмом можно назвать функцию, на вход которой поступает рассматриваемый объект, который необходимо отнести к определенному классу, а на выходе возвращается определенный класс, которому исследуемый объект соответствует. Если же говорить о понятийном аппарате классификационных моделей, именуемых деревьями решений, то тут важно обозначить, что по своей структуре деревья образуются вершинами и листьями. Вершины, называемые также узлами дерева, являются условиями, по которым проверяется соответствие объекта некоторому заранее определенному атрибуту. Листья являются конечными, терминальными элементами деревьев и содержат значения (то есть классы, иначе называемые найденными решениями). В процессе обучения дерева корректируются и подстраиваются параметры узлов дерева, а также значений в листьях с целью создания качественного классификационного алгоритма. Обучающими примерами для задачи формирования правильно работающего дерева становится некоторая заранее подготовленная группа объектов с известными классами.
Математически это можно записать следующим образом. Если задано конечное множество объектов X = {x1,…, xL} и множество алгоритмов A = {a1,…, aD}, а также некоторая бинарная функция, характеризующая потери l, такая что: A×X → {0,1}, l(a, x) = 1 тогда и только тогда, когда алгоритм ошибается на некотором объекте x. Количество ошибок алгоритма на выборке определяется по формуле
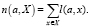(1)
При необходимости понять частотность ошибок алгоритма на некоторой выборке, можно воспользоваться следующей формулой:
v(a, X) = n(a, x)/|X|. (2)
Этот параметр частоты ошибок, совершаемых алгоритмом на контрольной выборке, называется качеством классификации.
Цель данной работы заключается в рассмотрении преимуществ и недостатков популярного метода решения задач классификации – деревьев решений, а также в определении возможных методов, позволяющих устранить или уменьшить недостатки деревьев решений.
1. Достоинства и недостатки использования деревьев решений в качестве классификаторов
a) Отбор признаков в вершинах узлов происходит автоматически
При использовании деревьев решений информативные признаки отбираются автоматически в процессе обучения. Этот факт делает метод классификации с помощью деревьев решений более привлекательным относительно других методов машинного обучения. Кроме того, в этом методе отсутствует дополнительный отбор признаков и существует возможность формировать собственные произвольные наборы признаков.
б) Интерпретируемость механизма принятия решений
В тех случаях, когда процесс работы алгоритма должен быть понятен для бизнеса или для верхнеуровневой оценки логики принятия решений в процессе его работы, есть возможность сформировать правила, по которым принимаются решения в понятной эксперту форме. Это свойство, вкупе с естественным языком предикатов в узлах деревьев, также может помочь найти ошибку в логике работы машинного алгоритма.
в) Управляемость и автономность вершин
В случаях, когда объекты тестовой выборки классифицируются неправильно, есть возможность переобучать те вершины, которые совершают ошибку. Также эта особенность позволяет обучать другим алгоритмам только части деревьев, используя более эффективные алгоритмы. Такой подход дает возможность управлять обучением, а также изменять результаты классификации определенных объектов, не затрагивая работу всего дерева.
г) Качество классификации зависит от баланса числа различных классов в обучающем множестве
Последовательность алгоритма создания дерева решений такова, что для начала процесса обучения в узел дерева выбирается максимально информативный предикат, который разбивает полученное множество на две части. Существует формула оценки информативности условия, размещенного в вершине:
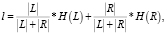(3)
где L и R – множества примеров, попадающие в результате разбиения по условию в левый и правый узлы дерева соответственно;
Оценка же информативности рассматриваемых тренировочных выборок производится по функциям H(L) и H(R), которые оцениваются с помощью энтропии Шеннона и индекса Джини.
Индекс Джини вычисляется по формуле
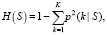(4)
где p(k|S) – доля экземпляров класса k в S;
K – количество классов;
S – некоторое множество обучающих объектов.
Особенность использования дерева решений такова, что в процессе обучения оно использует классы с большим числом тренировочных объектов, но пропускает те, которые содержат малое число примеров. В то время как для качественной классификации важно иметь баланс между классами в обучающей выборке. Можно рассматривать эту особенность дерева решений, с одной стороны, как достоинство, но в то же время это является и ее недостатком. В случае возникновения диспропорции в классах обучающей выборки, процесс обучения модели выполняется некорректно. А в качестве положительного аспекта этой особенности можно сказать, что вариация баланса между тренировочными объектами позволяет управлять обучением и корректировать его в нужную сторону.
д) Обучающая выборка уменьшается по экспоненциальной зависимости
В процессе обучения тренировочное множество последовательно разделяется на подмножества, проходя через каждую последующую вершину. Благодаря этому на каждом последующем вложенном уровне дерева находится меньше обучающих объектов, чем на предыдущем. При условии деления выборки на две равные части при каждой итерации прохождения через узел дерева, можно оценить размер выборки на самом низком уровне дерева (самая вложенная вершина). Если предположить, что уровень дерева – a, то размер выборки на вложенном листе станет в 2a раз меньше, чем ее начальный. Таким образом, при достижении более вложенных листов меньший размер обучающих примеров влечет за собой переобучение, и, следовательно, для корректного обучения дерева стоит подавать на вход модели значительно большие тренировочные множества.
2. Использование лесов решений для задач классификации
Использование леса решений для задач классификации может решить проблему переобучения. Итоговый ответ леса решений – это результат классификации нескольких деревьев, определенных голосованием (большинство предсказывают одно и то же). Положим, некоторое множество деревьев из леса решений, из которых каждое определяет объект x из множества X к одному из классов c, принадлежащего некоторому множеству классов Y. Применяется метод простого голосования, при котором для каждого класса c подсчитывается число деревьев, которые относят обозначенные объекты к данному классу. Если мы полагаем, что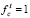 
, то дерево из лесов решений определяет рассматриваемый объект к классу c. Количество деревьев в данном случае можно вычислить по формуле
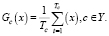(5)
Итоговым ответом, который дает классификатор леса решений, засчитывается класс, определенный большинством деревьев из леса: a(x) = arg maxc∈YGc(x). Независимость ошибок классификации при таком подходе является основой качественного распознавания объектов. В пограничном случае, при котором все деревья из леса ошибаются на одних примерах, использование леса решений не дает никаких дополнительных преимуществ перед использованием одного дерева решений. Верхняя граница ошибки обобщения, для оценки подобных случаев, может быть рассчитана по формуле
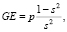(6)
где GE – ошибка обобщения;
p – средняя попарная корреляция между ошибками деревьев в лесу;
s – качество классификации каждого отдельного дерева [1].
Существует другой краевой случай – когда деревья леса обучаются с использованием одних и тех же тренировочных выборок с помощью одинаковых методов. В результате такого подхода деревья формируются идентично или с минимальными отличиями. Для того, чтобы избежать таких ситуаций, используется один из вариантов группы жадных алгоритмов – случайный лес [2]. В тех же случаях, когда необходимо достигнуть независимости ошибок внутри леса решений, используются отдельные специализированные методы (Bagging, XGBoost и другие). Рассмотрим самые популярные из них – Bagging и XGBoost).
При применении метода Bagging [3] каждое дерево из леса обучается на своем собственном сформированном случайно из общей выборки подмножества. Из негативных эффектов данного метода можно отметить исчезновение эффекта при увеличении численности тренировочного множества. При увеличении числа объектов все подвыборки становятся похожими друг на друга, в связи с тем, что они формируются из единого вероятностного распределения и влияние случайных отклонений при формировании таких подмножеств слабеет [4].
Метод Boosting использует в своем алгоритме назначение каждому примеру из тренировочной выборки (но в зависимости от степени сложности) определенные веса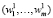 
. Веса при этом формируются вероятностно. Для них справедлива следующая формула:
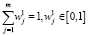. (7)
Начальное распределение весов устанавливается равномерным и равным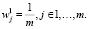 
Процесс алгоритма осуществляется следующим образом: сначала проходит обучение первое дерево. Следом классифицируются тренировочные обучающие примеры и их веса перераспределяются. Если обучающие примеры были определены верным образом, их вес снижается, а у классифицированных неверно – повышается. Второе и последующие деревья формируются с учетом скорректированных в тренировочной выборке весов, и так происходит до требуемого количества деревьев или опираясь на необходимую для данной модели ошибку классификации. Стоит принять во внимание, что при расчете информативности признака по формуле вместо доли объектов используется отношение суммы весов объектов, принадлежащих данному классу, к сумме весов всех объектов подмножества S:
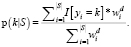(8)
Особенность применения алгоритма XGBoost к лесу деревьев заключается в последовательном обучении. Каждый шаг сопровождается вычислениями отклонений от предсказаний уже обученного леса на обучающей выборке. Каждая следующая модель, добавляемая в XGBoost, должна предсказывать эти отклонения. Благодаря этому, добавление предсказания нового дерева к лесу позволяет уменьшать среднее отклонение всей модели и это оптимизирует весь лес решений. Критерием добавления новых деревьев в лес является уменьшение ошибки, либо же добавление новых деревьев прекращается, если выполняется одно из правил ранней остановки [5].
3. Методы тестирования в машинном обучении при использовании деревьев решений
Для оценки качества алгоритма в деревьях решений можно применять метод скользящего контроля. Он помогает протестировать качество классификатора [6].
Начальное множество обучающих примеров разбивается на два подмножества, называемые тренировочным и контрольным. Сначала алгоритм проходит обучение на тренировочном множестве, затем рассчитывается число ошибок на контрольной выборке, и это число выполняет роль меры качества имеющегося алгоритма.
При оценке классификаторов таким способом невозможно выявить ошибки в формировании обучающего множества, а этот факт может оказаться критичнее, чем другие его негативные особенности. По существу, вся проблема исходит из того, что тренировочное и контрольное подмножества формируются на одном распределении, не всегда полно и корректно передающем начальные исходные данные, что создает ложные зависимости при реализации алгоритма машинного обучения. В таком случае оценка качества результирующей классификации может быть осуществлена двумя способами: на выборке, взятой из отличного от существующего независимого источника (лучшее решение данной проблемы), или оценив среднее значение разных источников. При таком способе важно помнить, что величина оценки будет напрямую зависеть от распределения примеров в выборке и их соотношения. Бывают прецеденты, при которых из тестовой выборки удаляются объекты, не изменяющие результаты классификации. Так улучшается качество классификации на тестовых объектах, но при этом ухудшается качество классификации на «боевых» данных. Не рекомендуется использовать такой прием еще и по той причине, что так можно ненамеренно изменить алгоритмы под тестовую выборку и они перестанут работать на других значениях, которые не похожи на тестовые.
4. Предлагаемые методы решения проблем при работе с деревьями решений
Приведем возможные способы решения проблемы, возникающей при уменьшении тренировочной выборки. Первый способ – случайное перемешивание. В качестве достоинств данного метода можно указать простоту реализации, а также минимальное значение используемой памяти. Для реализации данного способа после идентификации признака в узле дерева тренировочное множество делится на две группы объектов, а функция, по которой происходит это разбиение, зависит от обозначенного признака и порога. Математически эту закономерность можно описать так:
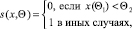(9)
где функция разбиения S(x, Θ), признака разбиения Θ1 и порог Θ2.
В зависимости от значения признака подмножества разделяются на левое и правое. Если функция равна нулю – определяются в левое подмножество, значение единица классифицирует объект в правое. Метод случайного перемешивания реализуется случайными изменениями подмножеств, в которое попадает объект. Для краевых случаев, когда левое подмножество становится больше правого по числу объектов, при этом не учитывая случайно перемешанные объекты, математическое ожидание тех из них, кто был перемещен из левого подмножества в правое, будет больше, чем для тех, кто перемещался из правого подмножество в левое. Результатом таких вероятностных изменений станет более равномерное распределение элементов множеств по вершинам, а также элиминация или уменьшение тех вершин, где число тренировочных примеров было недостаточно для корректного обучения модели.
Второй метод решения проблемы уменьшения тренировочного множества – это искусственное увеличение исходной выборки путем добавления схожих обучающих объектов. В данной работе уже упоминалось, что часть вершин деревьев решений при обучении может получить малое число тренировочных данных, в результате чего возникает переобучение. Решением этой проблемы может стать добавление новых, похожих на имеющиеся, примеров в тренировочную выборку. Недостатком данного способа может стать увеличение объема памяти, используемой при обучении, и если исходный набор данных достаточно большой, то в совокупности с временем добавления дополнительных данных этот способ может быть затратным по времени исполнения.
Заключение
В статье рассмотрена задача классификации с использованием алгоритма деревьев решений; описаны такие особенности: автоматический отбор признаков, интерпретируемость механизма принятия решений, управляемость и автономность вершин, зависимость от сбалансированности числа обучающих примеров разных классов, переобучение, экспоненциальное уменьшение обучающей выборки, разбалансировка. Предложены методы устранения недостатков, рассмотренных в статье.