Производство органических красителей имеет тенденцию интенсивного развития, отличается повышенными требованиями к качеству готовой продукции.
Из промышленно значимых сульфокислот 2-нафтола важной является кислота Шеффера, применяемая во многих отраслях промышленности.
Отметим, что производство кислоты Шеффера характеризуется экстремальными условиями труда. Например, исходное сырье, готовая продукция могут быть ядовитыми, обладать мутагенными и канцерогенными свойствами, что делает работу людей чрезвычайно опасной для их жизни и здоровья. Следовательно, на данных производствах необходимо принятие решений по минимизации обслуживающего персонала, т.е. по замене людей автоматизированными системами с использованием подсистем мобильных роботов-лаборантов. Неэффективность (низкая конверсия и производительность) технологического процесса производства кислоты Шеффера, случайный характер изменения гранулометрического состава 2-нафтола делают необходимой постановку задачи оптимизации производства кислоты Шеффера, решение которой с заданной гарантией обеспечивало бы выполнение технологических и технических ограничений [1].
Для решения проблемы удаления обслуживающего персонала из сферы вредного воздействия необходимо разработать структуру роботоавтоматизированной системы управления с использованием подсистемы робота-лаборанта [2, 3].
Анализ статических данных производства кислоты Шеффера в широком диапазоне возмущающих воздействий позволил выявить существование допустимой области управляющих воздействий U, определяемой заданной конверсией 2-нафтола в кислоту Шеффера.
Отметим, что при процессе сульфирования 2-нафтола необходимо обеспечить максимальную конверсию 2-нафтола на кислоту Шеффера.
Цели исследований: постановка задачи, гарантирующей оптимизацию процесса производства кислоты Шеффера; разработка структуры системы управления производством кислоты Шеффера с подсистемой робота-лаборанта.
Материалы и методы исследования
Задачу оптимизации процесса производства кислоты Шеффера на основе мягких вычислений сформулируем в следующем виде: для заданного гранулометрического состава 2-нафтола φ(r), вступающего в химическую реакцию, необходимо найти вектор управляющих воздействий u, т.е. найти расход Gs и концентрацию C0 серной кислоты, при которых конверсия 2-нафтола К достигает максимума, т.е.:
Q(u*) =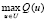 
,
где Q(u) =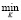 
K | 
(K | 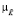u) ≥ mз, mз – заданное значение функции принадлежности конверсии 2-нафтола в кислоту Шеффера; при удовлетворении уравнений связи математической модели [4]; при выполнении технологических ограничений с заданной гарантией s ≤ 
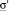, где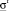 
– граница допустимого содержания побочных продуктов в готовом продукте, определяемая по формуле:
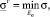
где Es = {s | m(s | u) ≥ es – область допустимости; es – уровень допустимости содержания побочных продуктов.
Область управляющих воздействий U определяется следующими ограничениями:
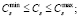
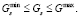
Оценим влияние гранулометрического состава 2-нафтола φ(r) на оптимальные управляющие воздействия Gs и C0 и величину конверсии 2-нафтола в кислоту Шеффера при гарантированном выполнении технологических и технических ограничений. В качестве примера на рис. 1 приведены результаты решения задачи оптимизации.
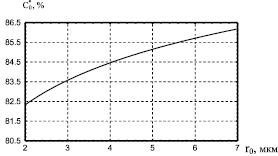
Рис. 1. Статическая характеристика C*0 от среднего размера частиц 2-нафтола
Результаты расчета показывают, что от величины среднего размера гранулометрического состава 2-нафтола, подаваемого на вход реактора, существенно зависят значения управляющих воздействий.
Отметим, что повышение концентрации серной кислоты приводит к уменьшению времени растворения частиц 2-нафтола, при этом увеличивается образование побочных продуктов, например дисульфокислот 2-нафтола. В результате этого снижается величина конверсии 2-нафтола в кислоту Шеффера.
Таким образом, оптимизация статических режимов процесса сульфирования позволяет повысить конверсию 2-нафтола в кислоту Шеффера и уменьшить содержание побочных продуктов. Также на технологический процесс могут воздействовать непредвиденные возмущения, которые не учитываются в математической модели, например изменения качества сырья, поступающего от разных поставщиков, изменения гранулометрического состава 2-нафтола в результате нестабильности процесса диспергирования. Вследствие этого возникает необходимость периодически осуществлять коррекцию «старого» оптимального режима с целью достижения заданных ограничений.
Химический анализ проб реакционной смеси, проводимый лаборантами в заводской или цеховой лабораториях, дает значительное время запаздывания, оказывает вредное воздействие на людей. Поэтому он проводится редко и не может быть использован при оперативном управлении технологическими режимами производства кислоты Шеффера при выполнении технологических ограничений с заданной гарантией.
Для реализации такого управления необходимо было разработать структуру роботоавтоматизированной системы управления процессом получения кислоты Шеффера с подсистемой робота-лаборанта, поскольку нужно достаточно часто измерять координаты адекватности K, s реактора. Кроме того, требуется измерять управляющие воздействия Gs, C0 и возмущающие воздействия j(r).
На рис. 2 показана блок-схема подсистемы робота-лаборанта, в состав которой входят: ЛСУ – локальная система управления технологическими режимами производства кислоты Шеффера; робот-лаборант, который получает и анализирует информацию с датчиков концентраций серной кислоты С0 и кислоты Шеффера К; система управления роботом-лаборантом, программное обеспечение которой должно осуществлять: восстановление гранулометрического состава 2-нафтола по косвенным измерениям, например по температуре реакционной смеси, частоте получения информации от датчика концентрации кислоты Шеффера; автоматизированная система управления технологическим процессом, которая осуществляет коррекцию математической модели, рассчитывает оптимальные управляющие воздействия.
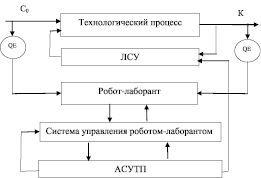
Рис. 2. Блок-схема подсистемы робота-лаборанта которые поступают на ЛСУ
Отметим, что расхождения значений выходных переменных технологического процесса, найденных экспериментально и рассчитанных по модели, могут быть вызваны сменой сырья, поступающего от разных поставщиков. Тогда необходимо проводить коррекцию коэффициентов математической модели. Таким образом, программное обеспечение роботоавтоматизированной системы управления должно содержать блок диагностики вариантов ситуаций.
Коррекция математической модели и пересчет оптимальных управляющих воздействий, гарантирующих выполнение технологических ограничений, осуществляются по результатам анализа концентрации кислоты Шеффера программным обеспечением системы управления робота-лаборанта.
При разработке роботоавтоматизированной системы будем учитывать следующие основные факторы. Отметим, что математическая модель, используемая в автоматизированной системе управления, скорректирована по опытным данным для данной партии сырья, полученным в лабораторных условиях с достаточно высокой точностью. Поэтому можем с большой степенью доверия относиться к коэффициентам математической модели.
Единственным нестационарным возмущением, которое не учитывается моделью, является изменение свойств 2-нафтола от партии к партии. Поэтому сама математическая модель, как правило, является адекватной объекту управления в течение технологического цикла выработки одной партии сырья. Однако точность решения задачи оптимизации с удовлетворением выполнения технологических ограничений с заданной гарантией существенно зависит от точности измерения гранулометрического состава сырья. Решение проблемы точности при определении j(r) связано с большими трудностями и требует значительных временных затрат. Проблема может быть решена путем создания адаптивного алгоритма оптимального управления при удовлетворении технологических ограничений с заданной гарантией, включающего в себя процедуру восстановления гранулометрического состава 2-нафтола по наблюдаемым параметрам технологического процесса, измеренным подсистемой «робот-лаборант».
Существенная неточность при расчете оптимального управления при гарантии выполнения технологических ограничений определяется ошибкой в измерении концентрации серной кислоты, подаваемой в реактор, которая может меняться при загрузке новой партии сырья. Точное измерение этого параметра методами экспресс-анализа невозможно. Таким образом, адаптивный алгоритм должен предусматривать возможность определения концентрации серной кислоты С0 по наблюдаемым роботом-лаборантом параметрам реактора, а также возможность использования точного значения С0, определяемого в заводской или цеховой лабораториях.
Наконец, причиной расхождения выходных переменных объекта, найденных экспериментально и рассчитанных по модели, может быть поступление сырья от разных поставщиков. В этом случае необходима коррекция коэффициентов математической модели. Таким образом, адаптивный алгоритм должен содержать блок диагностики вариантов ситуаций.
Опишем блок-схему роботоавтоматизированной системы управления, обеспечивающей выполнение технологических и технических ограничений с заданной гарантией.
Блоки 1 и 2 соответственно изображают технологический процесс производства кислоты Шеффера совместно с ЛСУ.
Блок 3 представляет алгоритм поиска оптимального управления, которое обеспечивает выполнение технологических ограничений с заданной гарантией.
В блоке 4 представлена математическая модель.
В блоке 5 сравниваются экспериментально полученные параметры адекватности модели и соответствующие параметры, рассчитанные по модели. Также в этом блоке принимается решение о целесообразности проведения корректировки математической модели или идентификации возмущающих воздействий. В качестве условия адекватности модели используется неравенство вида |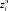
– zi| ≤ Dzi, i∈Iин, где Iин – множество индексов измеренных параметров; Dzi – допустимая погрешность.
Блок 6 оценивает параметры, измеренные роботом-лаборантом (блок 7), с расчетными значениями, затем определяется необходимость проведения корректировки математической модели.
В блоке 8 проводится проверка характеристик сырья.
Если характеристики сырья изменились, то в блоке 11 выбирается вектор параметров адаптации, блок 12 совместно с блоком 4 осуществляет коррекцию модели.
В блоке 9 осуществляется проверка проведения идентификации гранулометрического состава 2-нафтола. Если идентификация не проводилась, то блок 13 с блоком 4 восстанавливают состав 2-нафтола по экспериментальным данным.
Блок 10 проверяет, была ли корректировка значения концентрации серной кислоты, в противном случае блок 14 с блоком 4 восстанавливают значение С0.
Таким образом, блоки 8–10 являются блоками диагностики вариантов ситуаций.
При принятии решения о необходимости корректировки модели в блоке 6 необходимо учитывать следующий фактор: процесс коррекции связан с постановкой экспериментов, проведение которых требует определенных материальных затрат, в том числе затрат на проведение расчетов на ЭВМ. Следовательно, целесообразно сопоставить экономический эффект, полученный при коррекции математической модели, с вышеперечисленными затратами.
В предлагаемом алгоритме коррекции математической модели выбор момента времени tа ее коррекции основан на сравнительном анализе стоимости суммарных затрат Зм машинного времени на коррекцию модели и оптимизацию технологического процесса, стоимости затрат Зэ на проведение экспериментов и стоимости Зн потери 2-нафтола при процессе сульфирования, которые обусловлены тем, что технологический режим процесса производства кислоты Шеффера из-за неадекватности математической модели процессу не является оптимальным.
Стоимость затрат машинного времени на коррекцию модели и оптимизацию процесса при выполнении технологических ограничений с заданной гарантией вычисляется по формуле:
Зм =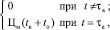 
где Цм – цена одного часа машинного времени; tк, tо – соответственно время расчета на ЭВМ, затраченное на решение задач коррекции и оптимизации.
Стоимость затрат Зэ на проведение экспериментов вычисляется по формуле:
Зэ =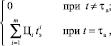 
где Цi – часовая ставка i-го лаборанта; m – количество лаборантов, принимающих участие в проведении экспериментальных исследований; 
– время, затрачиваемое i-м лаборантом на проведение экспериментальных исследований.
Стоимости потери 2-нафтола при процессе сульфирования определяются по формуле:
Зн =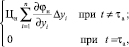 
где Цн – цена 2-нафтола; jн – непрореагировавший 2-нафтол.
Величину ?yi можно определить по формуле: Dyi =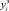 
(t) – yi(t), которая зависит от времени. Величина Зн является функцией текущего времени и времени проведения коррекции математической модели.
Значения величин Зм, Зэ и Зн, кроме других факторов, зависят от выбора момента времени tа, в который следует проводить коррекцию математической модели. Отметим, что целесообразным является выбор в качестве tа момента времени t, когда стоимость затрат Зм + Зэ станет соизмеримой с величиной Зн, т.е. Зм + Зэ = Зн.
В случае, если Зм + Зэ > Зн, стоимость затрат на потери 2-нафтола не превышает затрат на проведение экспериментов, то проводить коррекцию математической модели не следует.
Таким образом, определить следующий момент адаптации tа можно как наименьший корень следующего уравнения:
Ф(tа, t ) = | Зм(tа) + Зэ(tа) – Зн(tа, t) = 0.
Заметим, что для решения данного уравнения можно использовать методы недифференцируемой оптимизации [5].
Результаты исследования и их обсуждение
Поставлена задача оптимизации производства кислоты Шеффера при выполнении технологических и технических ограничений с заданной гарантией на основе мягких вычислений и приведены результаты ее решения. Разработана иерархическая АСУТП кислоты Шеффера с подсистемой робота-лаборанта. Приведены основные требования к роботу-лаборанту, используемому для оперативного определения С0, содержания побочных продуктов и контроля гранулометрического состава 2-нафтола. Разработан алгоритм коррекции математической модели.