Непрерывное развитие современной тех-ники подразумевает под собой разработку и внедрение технологий, позволяющих упростить осуществление тех или иных процессов, возникающих в повседневной жизни.
На сегодняшний день практически в каждом жилом помещении присутствуют счетчики контроля расхода электроэнергии, горячей и холодной воды, которые позволяют осуществлять контроль за процессом распределения соответствующих величин. Наличие подобных систем контроля подразумевает под собой взаимодействие потребителей с производителем услуг посредством отправки текущих показаний счетчиков в соответствующие коммунальные службы с некоторой периодичностью. Коммунальные службы, в свою очередь, с целью упрощения взаимодействия потребителей с производителем, используют специализированные сайты. Также компаниям требуются сотрудники, осуществляющие периодические проверки целостности счетчиков и корректности предоставляемых показаний.
Для упрощения передачи данных от потребителя к производителю услуг предлагается использовать специальное программное обеспечение для мобильных телефонов или смартфонов, что стало возможным благодаря динамическому развитию цифровых технологий. В частности, современные смартфоны обладают качеством фотографии, достаточным для использования получаемых изображений с целью распознавания определенных элементов. Более того, в настоящее время смартфон не является предметом роскоши и обладает высоким уровнем доступности и, как следствие, может значительно упростить процесс контроля показателей счетчиков.
Цель исследования: разработка, реализация и тестирование алгоритма для распознавания показаний бытовых счетчиков на изображениях, полученных с фотокамеры смартфона или мобильного телефона с помощью технологий компьютерного зрения.
Материалы и методы исследования
Алгоритм состоит из четырех основных этапов (рис. 1).
Детектирование циферблата счетчика. Данный этап осуществлялся с помощью определения контура циферблата, полученного детектором границ Кэнни [1]. Алгоритм для выделения контуров Кэнни основан на модели ступенчатых перепадов яркости. Задача нахождения оптимального детектора не может быть решена аналитически, только с помощью численных методов. Однако Кэнни показал, что хорошим приближением к оптимальному детектору ступенчатых перепадов является первая производная гауссиана. Для нахождения градиента изображения, сглаженного с помощью фильтра Гаусса, можно использовать оператор Собеля или – для более точных вычислений – оператор Собеля –Шарра [2], который определяется по формулам
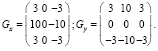
Тогда результат свертки изображения и матриц Gx и Gy будет являться соответствующими координатами вектора градиента. Далее по формулам можно получить G – модуль вектора градиента (1) и θ – угол направления градиента (2) для каждого пикселя.
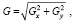(1)
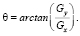(2)
При вычислении θ должна округляться до ближайшего значения к 0 °, 45 °, 90 °, 135 °.
Чтобы детектор имел высокую точность выделения границ, используются методы подавления точек, соответствующих немаксимальным значениям векторов градиента, и порогового преобразования с гистерезисом [1].
После выделения контуров мы следуем простой эвристике, которую можно обозначить следующими пунктами:
1. Циферблат должен быть расположен близко к центру изображения.
2. Циферблат должен иметь прямоугольную форму, то есть контуры циферблата, выделенные алгоритмом Кэнни, походят на четырехугольник при аппроксимации (в данной работе использовался алгоритм Рамера – Дугласа – Пекера [3]).
3. Ширина циферблата гораздо больше, чем его высота.
Используя данные замечания, можно отфильтровать все контуры так, чтобы остался только контур циферблата. Результат показан на рис. 2.
Поскольку снимок может иметь некоторые искажения перспективы (на рис. 2, в – циферблат имеет трапециевидный контур), следует произвести пространственную коррекцию. Для этой цели использовался алгоритм преобразования по четырем опорным точкам на изображении (рис. 2, в):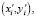 
i = 1,…,4. Далее, если обозначить матрицу преобразования как M, то коррекция перспективы выполняется по следующим формулам:
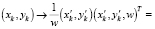
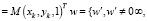иначе,
где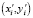 
и (xi, yi) – координаты i-го пикселя исходного и преобразованного изображений соответственно. То есть преобразование выполняется таким образом, чтобы опорные точки стали углами прямоугольника.
Рис. 1. Блок-схема работы алгоритма
а) б) в)
Рис. 2. а) исходная фотография счетчика, б) выделенные с помощью алгоритма Кэнни границы, в) изображение с отмеченным расположением циферблата
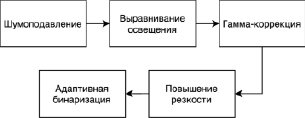
Рис. 3. Блок-схема алгоритма обработки изображения циферблата
Коррекция изображения циферблата. В данной работе предполагалось, что изображения получены с фотокамеры смартфона или мобильного телефона. Такие фотографии имеют множество дефектов, например цифровой шум, нарушения экспозиции, неровное освещение, геометрические аберрации или различные хроматизмы.
Для компенсации данных дефектов использовался метод повышения качества изображения для более четкого выделения цифр на циферблате. Предварительная обработка изображения выполнялась с помощью специально подобранных алгоритмов нормализации изображения, применяемых последовательно (рис. 3). Более подробно данный подход описан в [4].
Основная идея подавления шумов на изображении состоит в том, что яркость целевого пикселя в некотором блоке размером m пикселей берется как соотношение яркостей пикселей во всем блоке (количество пикселей в блоке лучше выбирать как квадрат некоторого натурального числа). Как правило, методы для удаления шумов отличаются друг от друга только способами выбора блока. В данной работе использовался метод NL-means [5], определяемый формулой вида
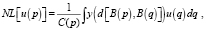
где d[B(p), B(q)] – евклидово расстояние между блоками с центрами p и q, y(x) – функция веса, C(p) – фактор нормализации, u(q) – значение неотфильтрованного пикселя изображения. Интеграл идет по всем точкам в блоке.
Для выравнивания освещения и регулирования баланса белого последовательно применялись алгоритмы SSR [6] и Gray World [7]. Фильтрация SSR вычисляется по формуле
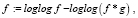
где f*g – результат свертки исходного изображения и двумерного фильтра Гаусса.
Алгоритм Gray World для трехканального изображения с интенсивностями R, B, G∈[0,255] по каждому пикселю выглядит следующим образом:
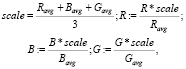
где Ravg, Bavg, Gavg – средние значения интенсивностей каждого из каналов изображения.
Гамма-коррекция [1, 8] используется для регулирования контраста и яркости изображения. Яркость каждого пикселя для скорректированного изображения определяется как
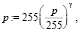
где γ – коэффициент гамма-коррекции.
Повышение резкости. Пусть g – гауссиан, e – единичный фильтр, a – коэффициент резкости, тогда, при выполнении перехода к свертке, получим формулу для повышения резкости f.
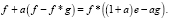
Тогда изображение с повышенной резкостью определяется по следующей формуле:
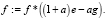
Бинаризация изображения [1]. Невозможно гарантировать, даже после выполненных выше преобразований, что яркости нужных нам областей будут схожи настолько, что можно будет подобрать глобальный коэффициент бинаризации. Поэтому в качестве алгоритма бинаризации была выбрана адаптивная бинаризация, которая зависит от яркости изображения в конкретном пикселе и размера окна бинаризации, а не от координат пикселя, как в случае глобальной бинаризации. Иначе говоря, в подходе адаптивной бинаризации рассматриваются пиксели в некотором окне, для которого некоторым способом определяется оптимальный коэффициент бинаризации. Например, по среднему значению интенсивностей пикселей.
Выделение цифровой информации из циферблата. Для выделения цифровой информации из циферблата использовалось бинарное изображение циферблата, полученное в предыдущем разделе. Дальше на нем необходимо выделить все контуры и отфильтровать слишком маленькие или слишком большие. Это представляется возможным по той причине, что циферблаты счетчиков имеют одинаковое количество цифр (шесть или семь) и поэтому при масштабировании изображений циферблатов к некоторому заданному разрешению контуры цифр будут соразмерны.
Тогда алгоритм выделения цифр можно описать следующим образом:
1. Приведение бинаризированного изображения циферблата к фиксированному размеру (рис. 4, б).
2. Выделение всех контуров на изображении (рис. 4, в).
3. Для каждого контура находим описывающий его минимальный прямоугольник.
4. Если ширина и высота прямоугольников лежат в некотором фиксированном диапазоне, то данный прямоугольник содержит искомую цифру (рис. 4, г).
Результат выделения показан на рис. 4, д.
Рис. 4. а) исходное изображение циферблата, б) изображение циферблата, полученное с помощью пороговой бинаризации, в) изображение с выделенными контурами, г) изображение с помеченными прямоугольниками с цифрами, д) полученные цифры в бинарном виде
Распознавание найденных цифр. Для распознавания цифр использовалась модель сверточной нейронной сети [9, 10]. Характерное свойство сверточной нейронной сети – устойчивость к искажениям, поворотам и переносам целевого объекта на изображении благодаря свертке с помощью локальных шаблонов. Такие шаблоны встраиваются в модель, формируя пространственные иерархии, как и объекты в реальном мире.
Поскольку модель сверточной нейронной сети обладает огромным количеством параметров, для ее обучения требуется массивный набор данных, репрезентативный относительно классов распознавания. Сформировать подходящий набор данных сложно, поэтому в качестве основы использовалась база рукописных цифр MNIST, дополненная изображениями для каждого класса, полученными с помощью аугментации [9] (рис. 5) изображений цифр с циферблата счетчиков.
Точность распознавания в метрике Accuracy [10] равна 98,58 % для тестовой выборки.
Рис. 5. Пример аугментации
Результаты исследования и их обсуждение
Детектирование циферблата основано на геометрических соображениях, однако циферблаты некоторых счетчиков могут им не удовлетворять. Например, счетчик может иметь циферблат с круглой формой или высота циферблата может быть больше ширины. В таких случаях имеет смысл разработать специализированную модель машинного обучения для детектирования циферблата на счетчике. Также возможны поиск и распознавание цифр напрямую на изображении счетчика, без детектирования циферблата. Однако последний способ не позволяет корректно обработать изображение.
В данной работе распознавание цифровой информации производится с помощью модели сверточной нейронной сети, обученной на наборе данных MNIST, дополненном изображениями цифр со счетчиков. Однако гораздо лучше будет сформировать новый набор данных, состоящий из цифр, характерных для циферблатов бытовых счетчиков. И хоть такие цифры представлены в машинописных шрифтах, при их извлечении могут образоваться некоторые искажения формы (как, например, у цифр, показанных на рис. 4, д). Поэтому часть набора данных, и достаточно большую, необходимо будет формировать вручную непосредственно из изображений счетчиков. Также необходимо будет учесть то, что для цифр могут использоваться различные шрифты, поэтому составить репрезентативный набор данных будет достаточно сложно.
Заключение
В данной работе был описан алгоритм, который помогает распознать цифровую информацию из изображений бытовых счетчиков, полученных с помощью фотокамеры смартфона или мобильного телефона. Алгоритм достаточно эффективен, в него включены методы, которые позволяют произвести подавление шумов и других искажений изображения, а также выполнить поворот и пространственную коррекцию циферблата бытового счетчика. Данные методы позволяют подготовить изображения для распознавания цифр.
Также были предложены пути дальнейшей разработки, которые, предположительно, позволят улучшить представленный алгоритм.