В настоящее время широкое применение получили пакеты прикладных программ, в алгоритмах которых реализованы численные методы динамики сплошных сред. Они позволяют эффективно моделировать особенности реальных физических процессов, происходящих в однородных жидкостях и газах, при проектировании технологических процессов в самых различных отраслях промышленности. Успешность применения их предопределена наличием общих теоретических моделей, адекватно описывающих процессы переноса массы, импульса и энергии в хорошо изученных гомогенных средах. Они лежат в основе универсальных и однозначных алгоритмов, которые научно обоснованы и поэтому модельные средства носят общий характер.
Движение гетерогенных сред связано с многообразием межфазных и внутрифазных взаимодействий, с различными структурными формами потока и соответствующими им новыми видами движения. Детальное описание физических процессов, необходимое для построения замкнутых математических моделей в таких условиях, становится чрезвычайно сложным даже для формулировки их состава и структуры. Феноменологические схематизации, применяемые обычно при недостатке научно обоснованных уравнений, также нуждаются в привлечении дополнительных понятий и параметров. Успешным примером такого подхода может служить представление гетерогенной среды многоскоростным континуумом с взаимопроникающим движением составляющих ее фаз или компонент, каждый из которых является континуумом со своими параметрами. Проблема многофазного движения в рамках этой многоскоростной модели решается заданием условий совместного движения частных континуумов и определением величин и соотношений, описывающих все их внутренние и межфазные взаимодействия. При этом необходимо описывать в каждом конкретном случае характер всех массовых, силовых и энергетических процессов, формирующих моделируемое многофазное течение [1].
В определенных условиях, при обоснованном сужении круга включаемых в рассмотрение физических эффектов такой методологический подход приводит к успешному решению множества важных прикладных задач. Но все они носят частный характер, поскольку обоснованы спецификой предметной области и не могут носить универсального, общего характера. Соответствующие им математические модели и вычислительные алгоритмы сохраняют неоднозначный характер, а получаемые результаты расчетов существенно зависят от обоснованности феноменологических соотношений и используемых данных экспериментальных исследований.
Термо-гидродинамика двухфазного потока на порядок сложнее даже однофазного потока однородной жидкости. Наличие движущейся и деформируемой межфазной поверхности и ее взаимодействие с обеими фазами требует значительной формализации, если руководствоваться существующими представлениями механики сплошных сред [2]. Достаточно высокая степень общности таких моделей связана с чрезмерными трудностями не только при получении частных решений. Гораздо раньше при построении математической модели необходимо обосновать условия, в которых протекают те или иные процессы. Большое разнообразие внутренних и внешних факторов затрудняет обычный параметрический анализ влияния размерных переменных, которыми характеризуются разнородные процессы. Вместе с тем существуют элементарные физические явления, сущность, а значит, и математическое описание которых сохраняются в любых условиях, где они могут проявляться независимо или совместно с другими физическими явлениями. [3].
Цель исследования: методическое обеспечение целевой спецификации сложных математических моделей при моделировании поведения перегретой эмульсии в неизотермическом турбулентном потоке эмульсии; обоснование состава модельных средств, формализующих сложные физические процессы, для адекватного представления реальных особенностей предметного области; применение системного анализа для использования элементарных физических явлений в качестве структурных элементов математических моделей.
Материалы и методы исследования
Выбор структуры математической модели обусловлен не только характером моделируемого физического явления, но и целями решаемой задачи. Поэтому спецификация сложной математической модели выполняется средствами системного анализа. Для этого выбираются структурные элементы (элементарные физические явления) модели исходя из общих теоретических представлений. Каждому такому элементу соответствует безразмерный критерий, однозначно отражающий его физическое содержание. Поэтому состав таких элементов может формироваться в соответствии с планируемой технологией, необходимой для получения продукции с определенным качеством. Идентификация функциональная формы взаимосвязей между выбранными элементами, исходя из априорной теоретической информации и данных экспериментальных исследований.
Результаты исследования и их обсуждение
Модели трансформации размеров дисперсной фазы в изотермическом турбулентном потоке. Элементарные физические явления дробления и связанные с ним коалесценция и седиментация определяют характер взаимодействия дисперсной фазы со сплошной средой [3, 4], а также структурные формы течения эмульсии несмешивающихся жидкостей. С воздействием турбулентного перемешивания сплошной среды связаны такие кинетические процессы, как коалесценция, дробление и седиментация. Они трансформируют спектр размеров дисперсной фазы в неустойчивых эмульсиях. В зависимости от соотношения исходного размера d0 и величины двух характерных размеров дисперсной фазы: dmax, максимального устойчивого по отношению к дроблению и dвзв, предельного устойчивого по отношению к гравитационной седиментации, модели неустойчивой эмульсии включают следующие комбинации элементарных физических явлений [5].
С другой стороны, структура турбулентности, в частности масштаб пульсаций скорости, также претерпевают изменения при взаимодействии с каплями дисперсной фазы различного размера. Так ранее было показано, что аномальные реологические эффекты крупнодисперсных эмульсий с неравновесной дисперсной обусловливают неадекватность гомогенных гидравлических моделей турбулентных течений. При интенсивной коалесценции эффект гашения пульсаций скорости инициирует релаксационные процессы в потоке эмульсий, которые проявляются на достаточно коротких участках трубопровода [6].
Модели кипения перегретых жидкостных эмульсий. Образование паровой фазы в объеме низкокипящих капель увеличивает их объем и, в определенных условиях, может способствовать их дроблению и появлению новых механизмов переноса теплоты в потоке эмульсии. Сферическая межфазная поверхность, которая ограничивает низкокипящую диспергированную жидкость, при образовании пузырьков паровой фазы, способна деформироваться и совершать собственные колебания. Крупномасштабные колебания плотности в этих условиях трансформируются в механическую энергию колебаний межфазной поверхности. Вынужденные колебания капель, в свою очередь, вызывают пульсационные движения жидкости, которой представлена внешняя, сплошная среда.
Возникновение колебаний при кипении как внутри двухфазного потока, так и колебания самого потока имеют не только важное научное значение. Для промышленных приложений интерес представляет локальный коэффициент теплопередачи, который значительно превышает прогнозируемую величину при отсутствии кипения. Образование пузырьков, которые вызваны кипением, обусловливает колебания, связанные с гидродинамическим потоком, индуцируемым вблизи поверхности нагрева. При этом распределение тепловых потоков носит сложный многофакторный характер, который формируется различными комбинациями гидродинамических и теплофизических процессов в каждом конкретном случае [7–9]. В свою очередь, механическая энергия пульсаций скорости в турбулентном потоке перегретой жидкости дополняет тепловую энергию, способствуя образованию жизнеспособных зародышей и росту пузырьков пара [10, 11].
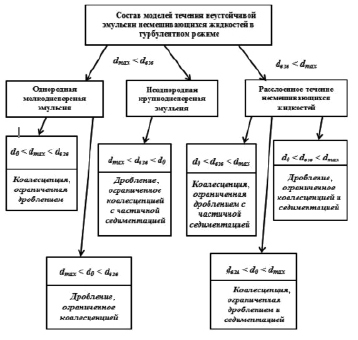
Рис. 1. Состав кинетических явлений в турбулентном потоке неустойчивых эмульсий несмешивающихся жидкостей
На рис. 2 представлены все комбинации механизмов разнородных физических процессов, которые могут происходить в турбулентных течениях жидкостных эмульсиях с фазовыми превращениями. Каждый из них по отдельности, это области А, В и С, достаточно хорошо изучен и обеспечен теоретически обоснованными модельными средствами. Проблемы возникают в условиях, когда для достижения технологического эффекта необходима их совместная реализация. Так в области АВ реализуются турбулентные течения неустойчивых эмульсий с трансформацией дисперсной фазы, используемые различными технологиями, в частности в пищевой, парфюмерной, химической и нефтехимической промышленности [5]. Области АС соответствуют физические процессы движения и кипящей однородной жидкости, которые происходят одновременно. Это широко используется для охлаждения и повышения эффективности теплоносителей в различном промышленном оборудовании [2, 12, 13].
Менее изученными остаются более сложные технологические процессы в неустойчивых жидкостных эмульсиях, связанные с фазовыми превращениями. В зависимости от теплофизических свойств кипение может происходить в одной из жидкостей, представляющей сплошную среду или дисперсную фазу эмульсии. В области ВС трансформация дисперсной фазы происходит в неподвижном объеме эмульсий, а в области АВС ситуация значительно усложняется тем, что пульсации скорости взаимосвязаны и с кинетическими процессами в дисперсной фазе, и с переносом теплоты в гетерогенной среде. Технологические потребности в совместном применении их на практике далеко не полностью обеспечены математическими моделями, адекватных структуре физических явлений, которые обеспечивают эффективность производственных процессов.
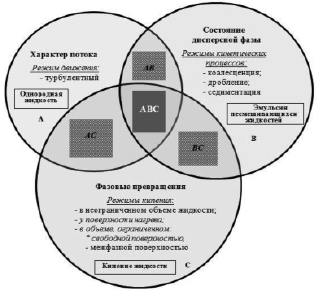
Рис. 2. Комбинации взаимосвязанных механизмов переноса теплоты
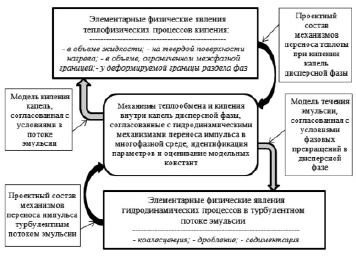
Рис. 3. Программный модуль согласования механизмов сложного процесса переноса
Интеграция частных математических моделей элементарных физических явлений. Аддитивные математические модели сложных физических процессов не могут адекватно отражать результат совместного протекания разнородных элементарных явлений. Взаимное влияние их друг на друга обусловливает нелинейный характер связывающих их уравнений, который не поддается теоретическому описанию. Простого добавления программных кодов (дополнительных соотношений) для расширения отдельных модулей существующих стандартных программ недостаточно, поскольку это затрагивает другие модули и структуру взаимосвязей между ними. В конечном итоге каждый полученный эвристическим путем состав и структура такой модели нуждается в верификации и оценивании ее эмпирических констант на основе априорных данных моделируемого физического процесса [14].
На рис. 3 представлена функциональная схема программного модуля согласования совместных механизмов моделируемого сложного теплофизического процесса, который позволяет согласовать механизмы теплообмена и кипения жидкостной эмульсии с гидродинамическими механизмами переноса импульса в многофазной среде. Основная задача модуля состоит в обеспечении согласования модельной структуры взаимосвязанных механизмов разнородных физических процессов с характерными особенностями предметной области. Процедура согласования наряду с идентификацией формы математической модели предусматривает оценивание модельных констант, величина которых отражает вклад каждого элементарного физического явления.
Целевое привлечение элементарных физических явлений и обоснованное ограничение их совокупности полезно при формировании структуры новых технологических процессов, а в последующем и при обосновании конструктивных параметров промышленного оборудования [15]. Физически обоснованные математические модели существенно снижают сложность как теоретического описания и анализа сложных процессов, так и выбора режимов и средств решения соответствующей технической задачи.
Заключение
Создание необходимых условий и контроль над завершенностью физических, химических и термодинамических превращений является сложной задачей, решить которую на стадии проектирования можно только на основе численного моделирования и специализированных математических моделей. Для этого недостаточно пакетов прикладных программ в рамках формализованных CFD кодов на основе моделей механики сплошных сред. Технологические операции в неустойчивых жидкостных эмульсиях связаны с различными механизмами кинетических процессов и с учетом дискретной структуры рабочих сред. Большое число переменных, необходимых для формализации поведения многофазных сред, усложняет математические модели, и обычно их упрощают с помощью процедур осреднения. Редукция большого числа размерных переменных, влияние которых неоднозначно из-за возможного участия их в нескольких элементарных физических явлениях к ограниченному количеству безразмерных критериев, значительно упрощает состав математической модели. В отличие от формальных регрессионных соотношений между многочисленными константами и размерными переменными, критериальная модель отражает реальное физическое содержание моделируемого процесса. Она пригодна для расширения состава и согласования механизмов элементарных физических явлений в соответствии с характерными особенностями предметной области.



