Для моделирования различных динамических систем достаточно часто используются интегральные модели [1, с. 4–5, 163–164]. Если параметры системы не меняются во времени, то такая система называется стационарной, и ее поведение описывается интегральным уравнением Вольтерра I рода с разностным ядром [2, с. 109–128]:
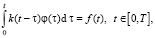(1)
где k(t) – импульсная переходная функция (ИПФ) системы; φ(τ), f(t) – ее входной и выходной сигналы. Для физически реализуемой системы выполняется условие k(t) = 0 при t < 0. Задача непараметрической идентификации системы (1) заключается в вычислении оценки для ИПФ k(t) по измеренным значениям входного и выходного сигналов идентифицируемой системы.
На практике для идентификации стационарных систем часто (в силу своей простоты) применяется схема, в которой на вход идентифицируемой системы подается (в момент t = 0) ступенчатый сигнал, амплитуда которого постоянна. Заметим, что если амплитуда равна 1, то такой сигнал называется функцией Хевисайда (выполнение этого условия предполагается в дальнейшем). Для такого входного сигнала можно показать [2, c. 163–164], что:
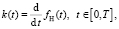(2)
где fН(t) – выходной сигнал (реакция системы), если на вход подана функция Хевисайда. Несмотря на хорошо разработанные алгоритмы численного дифференцирования, использование (2) на практике связано с той же проблемой некорректности, что и при решении уравнения (1), так как операция дифференцирования является некорректно поставленной задачей [3]. Чаще всего это проявляется в неустойчивости операции дифференцирования, когда даже небольшой уровень шума регистрации выходного сигнала вызывает очень большие ошибки в полученной (на основе (2)) оценке ИПФ. Для получения устойчивой оценки ИПФ зарегистрированный (с ошибками измерения) сигнал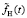 
первоначально сглаживают (фильтруют), а затем применяют операцию дифференцирования. Часто на практике для этих целей используют (из-за их простоты построения и наличия соответствующего программного обеспечения в ряде математических пакетов) сглаживающие кубические сплайны (СКС) [4; 5]. К сожалению, в получаемых оценках ИПФ при высоком уровне шума (10–15 %) присутствуют (даже при оптимальных параметрах сглаживания) значительные ошибки идентификации (особенно при малых и больших значениях времени t). Поэтому целью данной статьи является разработка способов уменьшения ошибки идентификации путем:
– построения СКС с заданием левого и правого краевых условий в виде значений первых производных;
– использования при построении СКС качественной априорной информации о поведении выходного сигнала fН(t) или ИПФ идентифицируемой системы.
Материалы и методы исследования
Предположим, что зарегистрированный в узлах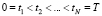 
зашумленный выходной сигнал 
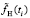допускает представление:
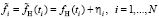, (3)
где ηi – шум с нулевым средним и дисперсией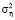 
. Для сглаживания зашумленных значений 
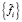обратимся к сглаживающим кубическим сплайнам (СКС). Напомним, что сглаживающий кубический сплайн Sf(x) на каждом отрезке 
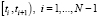представляет собой полином третьей степени вида [4; 5]:
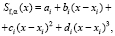(4)
и является дважды непрерывно дифференцируемым на всем интервале [0, T]. Для однозначного вычисления коэффициентов СКС ai, bi, ci, di задают левые и правые краевые условия. Например, естественные краевые условия определяют нулевые значения вторых производных в узлах t1, tN, т.е.
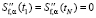. (5)
Показано [4; 6], что СКС с естественными краевыми условиями доставляет минимальное значение функционалу:
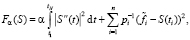(6)
где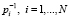 
– весовые множители. Меняя параметр сглаживания α в интервале [0, ∞), можно изменять ошибку сглаживания. Величину параметра сглаживания, минимизирующего среднеквадратическую ошибку (СКО) сглаживания, назовем оптимальным параметром и обозначим αopt. Алгоритмы оценивания αopt рассмотрены в работах [6, с. 62–67; 7].
К сожалению, задание краевых условий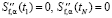 
может привести к значительным ошибкам идентификации (ошибкам дифференцирования СКС) при малых и больших значениях аргумента СКС. Для иллюстрации этого факта на рисунке, а показаны значения «точной» ИПФ (сплошная кривая) и оценки 
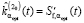(штриховая кривая), вычисленной дифференцированием СКС, построенной при α = αopt и краевых условиях (5), при этом шум измерения имел относительный уровень 0.15.
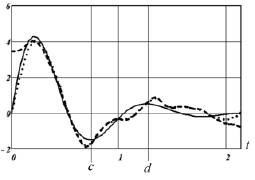
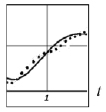
а) б)
Оценки импульсной переходной функции
Видна большая ошибка идентификации при малых значениях t: вместо нулевого значения при t = 0 оценка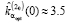 
, но по мере увеличения аргумента влияние левого краевого условия уменьшается. Аналогичную ошибку можно наблюдать для значений времени, близких к правому концу интервала: 
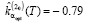. Для уменьшения таких ошибок необходимо задать краевые условия, исходя из специфики решаемой задачи. Например, для ряда динамических систем (колебательные звенья второго порядка и др.) известно, что k(0) = 0, k(T) = 0. Учитывая эту и подобную априорную информацию, целесообразно краевые условия задать значениями первой производной, что, несомненно, приведет к увеличению точности идентификации. Поэтому перейдем к построению алгоритма вычисления коэффициентов сплайна при таких краевых условиях.
Составим систему уравнений (используя результаты работы [6]) для вычисления значений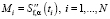 
, в случае, когда слева в качестве краевых условий будут задаваться величины первых производных:
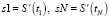. (7)
Систему уравнений можно представить в следующем виде:
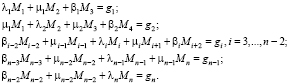(8)
Коэффициенты системы определяются соотношениями, в которых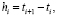 
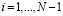– шаги между соответствующими узлами сетки
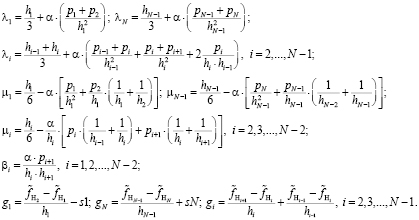
После вычисления решения этой системы коэффициенты сплайна определяются выражениями:
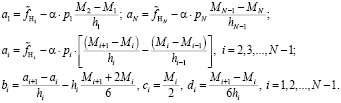
Очевидно, что, вычислив коэффициенты СКС, можно найти первую производную для любого значения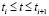 
:
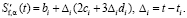
На рисунке, а точечной кривой показаны значения ИПФ, вычисленной как производная СКС с краевыми условиями (7). Видно, что точность этой оценки (в граничных точках интервала) существенно выше, чем при использовании краевых условий (5).
Заметим, что и для краевых условий (7) параметр сглаживания можно эффективно выбирать, используя статистический алгоритм, построенный на основе критерия оптимальности и изложенный в работе [6, с. 62–67].
Результаты исследования и их обсуждение
Дескриптивный алгоритм сглаживания. На практике у экспериментатора имеется определенная информация (априорная или апостериорная) о поведении на отдельных интервалах времени либо самой ИПФ, либо выходного сигнала fН(t) идентифицируемой системы. Очевидно, что учет такой нетривиальной достоверной информации может также привести к уменьшению ошибки идентификации ИПФ. К сожалению, изложенный выше алгоритм вычисления коэффициентов сплайна не позволяет учитывать такую информацию. Изложим подход, позволяющий при построении сплайна учесть некоторые формы задания априорной информации.
Запишем функционал (6) и имеющуюся априорную информацию в дискретном виде через значения сглаживающего сплайна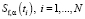 
, которые представим в виде вектора sα с проекциями 
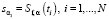. Можно показать, что слагаемое 
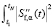в выражении (6) можно представить выражением:
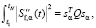(9)
где матрица Q имеет размеры N×N и определяется как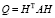 
. Элементы матрицы H размером 
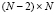определяются выражениями:
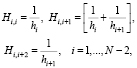
а элементы трехдиагональной матрицы A размером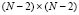 
определяются выражениями:
;
.
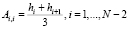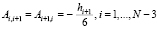Введя диагональную матрицу весов P с элементами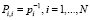 
, функционал (6) (с учетом (9)) можно записать в виде:
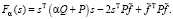(10)
Перейдем к построению системы ограничений, позволяющей задать априорную информацию об идентифицируемой ИПФ. Наиболее универсальной формой задания (хорошо согласующейся с функционалом (10)) является система линейных неравенств вида:
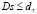(11)
где размеры матрицы D и вектора d зависят от вида априорной информации. Например, информацию о знаках ИПФ или ее производных можно задать с помощью конечных разностей соответствующего порядка [8]. Пример такого задания приводится ниже.
Тогда значения дескриптивного (от глагола «описывать») сглаживающего сплайна определяются как решение задачи условной минимизации:
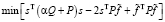(12)
при ограничениях:
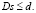(13)
После решения этой вариационной задачи по полученным значениям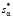 
дескриптивного сплайна строится интерполяционный сплайн, производная от которого является оценкой для идентифицируемой ИПФ динамической системы.
Заметим, что в состав многих математических пакетов входят модули (например, в пакете MathCAD это функция Minimize и блок решений Given), позволяющие решать задачи условной оптимизации большой размерности [9].
Результаты численных исследований. Для исследования изложенного подхода к построению дескриптивного сплайна вернемся к ранее рассмотренному примеру. Из рисунка, а видно, что на интервале [c, d] построенная оценка ИПФ с условиями (7) (точечная кривая кое-где совпадает со штриховой кривой – краевые условия (5)) должна быть неубывающей функцией. Колебания этой оценки обусловлены влиянием остаточного (после сглаживания) шума измерения. Поэтому зададим эту информацию (по сути дела уже апостериорную) в виде системы ограничений (13) для проекций вектора ИПФ с номерами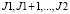 
, соответствующих интервалу [c, d]. Тогда ненулевые элементы матрицы D с размерами 
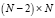задаются через конечные разности второго порядка следующими соотношениями:
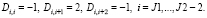
Остальные элементы матрицы D равны 0. Вектор d размерности N – 2 является нулевым вектором. Очевидно, что описанные ограничения соответствуют разностям второго порядка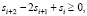 
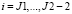, т.е. значения сплайна для индексов 
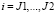не убывают.
На рисунке, б в увеличенном масштабе точечной кривой показаны значения оценки ИПФ, полученной дифференцированием интерполяционного сплайна, построенного по значениям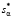 
, которые являются решением вариационной задачи (12), (13). Видно, что новая оценка ИПФ на интервале [c, d] является неубывающей функцией, что соответствует физическим представлениям об идентифицируемой ИПФ, и эта оценка имеет меньшую ошибку идентификации.
Заключение
Предложенный подход к учету как априорной, так и апостериорной информации об идентифицируемой функции позволяет существенно повысить точность идентификации, но, самое главное, построить оценку, которая удовлетворяла бы ограничениям, сформированным на основе имеющейся у экспериментатора информации об идентифицируемой ИПФ.