Известно, что силы трения, определяющие в значительной степени интенсивность износа деталей цилиндропоршневой группы и потери энергии на преодоление трения, возникают под действием давления газа между уплотнительными кольцами и стенкой цилиндра, последнее, как следствие, оказывает непосредственное влияние на к.п.д. компрессорных машин. При этом потери на трение, в частности в узлах, функционирующих без смазки, достигают существенного значения, и поэтому изучение их заслуживает пристального внимания. Учитывая вышеизложенное, проблема трения поршневых бессмазочных уплотнений не утратила своей актуальности и является одной из ключевых проблем в области поршневых машин. Исследование обозначенной выше проблемы направлено на возможность снижения энергетических потерь, износа и увеличения срока службы уплотнений, что, в свою очередь, приведет к межремонтному пробегу машин [1].
В трибологии существует ряд фундаментальных методик для расчета коэффициента трения, линейного износа и прогнозирования ресурса работы узлов трения из полимерных материалов. Далее представлены некоторые базовые методики для расчета величины износа и скорости изнашивания материала.
Одним из основных уравнений, посредством которого в зарубежной практике рассчитываются величины линейного износа (Δb, мм), как полимерных уплотнительных колец, является уравнение Арчарда [2]. Данное уравнение позволяет учитывать и скорость скольжения (ϑ, м/с), и среднее нормальное контактное давление (Рк.ср, МПа), и время работы сопряжения (τ, ч):
Δb = K•ϑ•Рк.ср•τ, (1)
где параметр K (коэффициент изнашивания) определяется экспериментально и зависит от нагрузки, плотности материала и его твердости [2].
Используя расчетные уравнения в работе [3], можно дать инженерный расчет на износ для различных случаев контакта, с учетом нормального контактного давления (pk), модуля упругости (E), коэффициента трения (fтр), параметра прочности (Go), коэффициента гистерезисных потерь (αг), коэффициентов, зависящих от природы трения (t, t0, ty) и эмпирических коэффициентов (K2, Ktv, K). В частности, приводится зависимость для приработанных деталей любой конфигурации, которая в случае упругого контакта имеет вид:
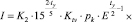
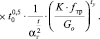 (2)
(2)
Анализ достаточно большого числа научных исследований износостойкости различных материалов в условиях граничного трения и трения без смазки показывает, что в общем случае скорость изнашивания (I) может быть выражена эмпирической зависимостью (k – коэффициент изнашивания, характеризующий материал пары и условия изнашивания; m = 0,5–3, n = 1 для большинства пар трения), учитывающей режим эксплуатации узла (Pk и v – нормальное контактное давление и скорость скольжения соответственно), вида:
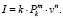 (3)
(3)
Из формул, приведенных выше, очевидно, что одним из основных составляющих является контактное давление (pk). Здесь следует подчеркнуть, что именно от точности определения контактного давления зависит правильность расчета износа и определения ресурса работы уплотнения. В связи с этим приоритетным становятся исследование давление газа, действующего на каждый из элементов уплотнения, и взаимосвязь давления с силой, прижимающей элемент к цилиндру, и определяющей его износ. Ниже приведены основные известные методики по определению контактного давления в цилиндропоршневой группе.
Материалы и методы исследования
Уплотнительный эффект колец основан как на плотном прилегании их к внутренней поверхности цилиндра и к стенкам поршневых канавок, так и на лабиринтном действии набора колец. Давление, действующее на внутреннюю поверхность кольца, превышает среднее давление, действующее на внешнюю поверхность кольца, и создает основное усилие, прижимающее кольцо к зеркалу цилиндра. Чем больше перепад давления на поршневом кольце, тем сильнее оно прижимается к рабочей поверхности цилиндра. В первом приближении можно считать, что сила прижатия i-го кольца к стенке цилиндра определяется по формуле [4].
pпр.i = 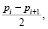 (4)
(4)
где pпр.i – сила прижатия к рабочей поверхности цилиндра;
pi – pi+1 – давления до и после уплотнения.
При исследовании контактного давления уплотнительных колец в работе [5] экспериментально была доказана необходимость введения поправочного коэффициента β, который учитывает распределение давления по высоте кольца и определяется по формуле:
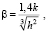 (5)
(5)
где k – коэффициент, учитывающий свойства материала и характер изменения давления в цилиндре при постоянном и переменном давлении, равен 1,0 и 1,5 для непропитанного графита типа АО-1500 и 2П-1000; 2,0 и 3,0 для пропитанного графита типа АО-1500С05; 2,5 и 3,5 для фторлоновых композиций типа Ф4К20 и Ф4К15М5.
Учитывая поправочный коэффициент β, перепад давления на поршневом кольце определяется по формуле:
pпр.i = 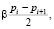 (6)
(6)
где β – коэффициент распределения давления по высоте уплотнения.
В работе [6] автор при расчете контактного давления, помимо перепада давления на поршневое кольцо, учитывает давление сил от собственной упругости, которое зависит от свойств материала кольца, с учетом последнего формула имеет вид:
pk = pe + 0,5Δpд, (7)
где pe – давление от сил собственной упругости колец, pд – перепад давления на кольцо.
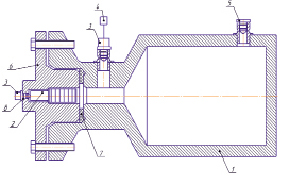
Рис. 1. Принципиальная схема экспериментального стенда: 1 – рабочая камера; 2 – испытуемый поршень; 3 – датчик давления; 4 – микрометр; 5 – датчик давления; 6 – крышка; 7 – уплотнение; 8 – отверстие для выхода газа
Величина контактного давления определяется напряжениями, возникающими при деформации уплотнительного элемента, устанавливаемого с натягом на герметизируемую поверхность, усилием упругого элемента и воздействием давления рабочей среды. В общем виде расчет контактного давления осуществляется по формуле:
Pk = Pп.д. + Pe+ PД, (8)
где Pп.д. – полуразность давлений, Pe – давление от сил собственной упругости колец, PД – напряжения, возникающие при деформации.
В теории манжетного уплотнения автор [5, с. 350] приводит формулу для расчета контактного давления манжетного уплотнения:
Pk = π*D*b*Δp, (9)
где D – диаметр цилиндра, b – ширина трущейся части манжеты, Δp – перепад давления.
Наружный диаметр борта манжеты в свободном состоянии несколько больше диаметра цилиндра D, и рабочая поверхность манжеты имеет небольшую конусность. При введении поршня с манжетой в цилиндр манжета деформируется и прижимается силой собственной упругости к рабочей поверхности цилиндра, создавая начальную герметичность.
Результаты исследования и их обсуждение
В целях экспериментального определения контактного давления манжетного уплотнения на стенки цилиндра был разработан экспериментальный стенд (рис. 1). Суть эксперимента заключалась в следующем: в крышку (6) устанавливался поршень с одним манжетным уплотнением. Затем в рабочую камеру (1) нагнетался газ до 5,2 МПа. В момент достижения давления газа в рабочей камере 5 МПа фиксировалось давление газа после манжеты при помощи датчиков давления (4). Эксперимент повторялся для поршня с двумя и с тремя манжетными уплотнениями.
По результатам экспериментального определения контактного давления цилиндропоршневого уплотнения были построены графики изменения перепада давления по высоте поршня, при давлении газа в цилиндре: 10, 5 и 3 МПа.
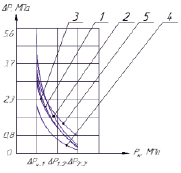
Рис. 2. График изменения перепада давления на манжетное уплотнение при давлении в цилиндре 10 Мпа: 1 – кривая, построенная по формуле (4); 2 – кривая, построенная по формуле (6); 3 – кривая, построенная по формуле (7); 4 – кривая, построенная по формуле (8); 5 – кривая, построенная по формуле (9)
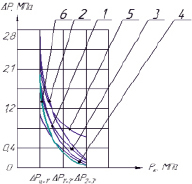
Рис. 3. График изменения перепада давления на манжетное уплотнение при давлении в цилиндре 5 Мпа: 1 – кривая, построенная по формуле (4); 2 – кривая, построенная по формуле (6); 3 – кривая, построенная по формуле (7); 4 – кривая, построенная по формуле (8); 5 – кривая, построенная по формуле (9); 6 – кривая, полученная экспериментально
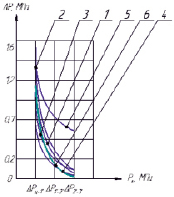
Рис. 4. График изменения перепада давления на манжетное уплотнение при давлении в цилиндре 3 Мпа: 1 – кривая, построенная по формуле (4); 2 – кривая, построенная по формуле (6); 3 – кривая, построенная по формуле (7); 4 – кривая, построенная по формуле (8); 5 – кривая, построенная по формуле (9)
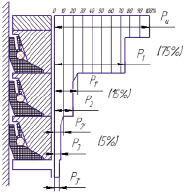
Рис. 5. Типичное распределение давления газа в уплотнении поршня простого действия
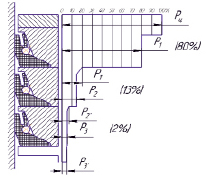
Рис. 6. Типичное распределение давления газа в уплотнении поршня простого действия
Дополнительно был проведен сравнительный анализ типичного распределения давления газа в уплотнении при использовании поршневых колец, согласно экспериментальным данным, полученным в работе [6, с. 333] (рис. 5), и при использовании манжетного уплотнения, согласно данным, полученным экспериментально при помощи стенда, описанного выше (рис. 6). Мы видим, что при использовании манжеты в качестве уплотнения газ теряет 80 % энергии, что в 5 % больше при использовании поршневого кольца в качества уплотнения.
Заключение
Как видно из построенных выше графиков, значения контактного давления отличны друг от друга в зависимости от методики расчета. Это свидетельствует о том, что для получения более точного значения контактного давления необходимо проводить натурный эксперимент. При этом дополнительно стоит учесть, что величина контактного давления в процессе износа будет изменяться (а именно, уменьшаться), так как площадь контакта будет увеличиваться.



