В настоящее время лесотранспортные операции и затраты на их проведение оказывают существенное влияние на весь лесозаготовительный процесс и рентабельность работы предприятия. В этих условиях решение инженерных задач на транспорте и определение технико-экономических показателей работы лесотранспортных машин приобретает особую значимость для повышения эффективности транспортно-переместительных операций.
На протяжении долгого времени многими исследователями разрабатывались и совершенствовались методы тяговых расчетов для определения показателей движения лесовозных автопоездов. Значительный вклад в разработку подобных методов был внесен исследователями и учеными ЦНИИМЭ и других исследовательских и научных учреждений [1, 2]. Исследованиями в области повышения эффективности лесотранспортных операций и определения показателей и режимов движения лесовозных автопоездов в различных условиях эксплуатации занимались следующие специалисты и ученые: В.И. Алябьев, Б.А. Ильин, О.Н. Бурмистрова, В.К. Курьянов, А.А. Камусин, А.В. Скрыпников, С.И. Сушков и др. [3–6]. Разработкой и совершенствованием методов тяговых расчетов и моделированием движения лесовозных автопоездов – Б.И. Кувалдин, В.И. Скрыпник, И.Р. Шегельман и др. [1, 2, 7, 8].
Разработанные методы и программы [1, 7] использовались в Системе автоматизированного проектирования автопоездов, при проектировании лесотранспортных путей, при выборе оптимального типа автопоезда, при многовариантном проектировании и в учебном процессе. На основе расчетных экспериментальных исследований, в процессе которых определялись фактические и расчетные показатели движения, дана оценка точности и адекватности расчетных показателей движения (скорости и времени движения, пройденного расстояния, режимов движения и др.). Доказано, что обеспечивается достаточная точность и адекватность результатов в сравнении с фактическими показателями, вследствие учета всех основных условий, влияющих на показатели движения автопоездов.
В то же время в связи с появлением новых типов и моделей лесовозных автопоездов и необходимостью учета всех факторов, оказывающих влияние на их режимы движения, а также расширением круга решаемых задач и упрощения расчетов без снижения их точности полученные методы и зависимости тяговых расчетов требуют дальнейшего совершенствования и развития.
Цель исследования: разработать алгоритм и методику расчета для определения показателей неустановившегося движения лесовозных автопоездов с механической трансмиссией.
Материалы и методы исследования
При условии аппроксимации кривой тяговой характеристики в рабочем диапазоне двигателя семейством кривых вида
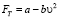, (1)
где a и b – эмпирические коэффициенты для определения скорости движения, выведены зависимости, дающие возможность определять скорость в конце участка длиной S с учетом начальной скорости движения υ0.
Расчетные формулы имеют вид
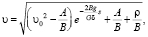(2)
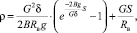(3)
где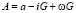 
; ι – продольный уклон; G – вес автопоезда, кгс; S – пройденное расстояние, м; ω – коэффициент сопротивления движению; δ – коэффициент учета инерции вращающихся масс; Rв – радиус вертикальной кривой, м; 
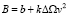; k – соответственно, коэффициент сопротивления воздушной среды для автомобиля; Δ – коэффициент, учитывающий дополнительное сопротивление от прицепов; Ω – лобовая площадь автомобиля, м2.
Формула (2) применяется для определения скорости движения автопоезда на вертикальных кривых. На прямолинейных в профиле участках последний член в формуле (2), т.е.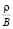 
, исключается, так как на прямолинейных участках Rв = ∞, следовательно, ρ равно 0.
Сформированы таблицы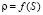 
для всех передач КПП. При этом радиус кривой Rг принят равным 1000 м. При большем или меньшем значении Rг определяется по формуле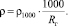 
В таблице приведены значения ρ при движении автопоезда на базе МАЗ-6303-26.
С использованием таблиц значительно облегчается определение скорости движения (с работающим двигателем, торможением двигателя и моторным тормозом). Упрощаются расчеты при проектировании и решении технико-экономических задач на транспорте, при выборе различных типов автопоездов и т.д.
Результаты исследования и их обсуждение
Чтобы избежать формирования таблиц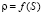 
и упростить зависимости для определения υ, не снижая точности расчетов, зависимость для определения ρ на вертикальных кривых преобразуется исходя из следующих предпосылок.
Дифференциальное уравнение движения при аппроксимации тягового усилия от скорости движения имеет вид
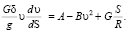(4)
В дифференциальном уравнении (4), решением которого является зависимость (6), обозначения те же, что и в формулах (2)–(3).
На заданном участке длиной S среднеинтегральное значение величины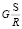 
в диапазоне от 0 до S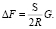 
Следовательно, уравнение (4) может быть представлено в виде
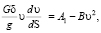(5)
где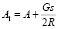 
.
Значения ρ при движении автопоезда на базе МАЗ-6303-26 в грузовом направлении с полной нагрузкой на 7 передаче КПП
|
S |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
|
ρ |
1,278 |
5,138 |
11,54 |
20,479 |
31,941 |
45,91 |
60,382 |
81,334 |
102,775 |
126,633 |
|
S |
100 |
120 |
130 |
140 |
150 |
160 |
170 |
180 |
190 |
200 |
|
ρ |
152,95 |
181,71 |
212,875 |
246,45 |
282,41 |
320,76 |
361,47 |
404,53 |
449,93 |
497,67 |
В этом случае расчетная зависимость (5) упрощается.
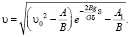(6)
Расхождение в результатах расчетов не превышает 0,08 %, т.е. по точности расчетов зависимости (6) и (2) фактически равноценны; в практических расчетах при отсутствии таблиц ρ предпочтительнее использовать зависимость (6).
На прямолинейных в профиле участках для определения скорости движения, А1 (так как Rв = ∞) не определяется в расчетах, а принимается значение A, принятое в формуле (2).
Для определения показателей движения на прямолинейном в профиле участке, исходя из формулы (2), при отсутствии ρ, выведена зависимость для определения расстояния S на прямолинейном в профиле участке, которое пройдет автопоезд при изменении скорости от υ0 до υк.
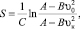(7)
где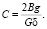 
На вертикальных кривых исходя из зависимостей (1), (2) вывод расчетных формул для определения S невозможен.
При от υ0 до υк
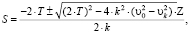(8)
где T – среднеинтегральное тяговое усилие на прямолинейном в профиле участке с уклоном, равным уклону в начальной точке вертикальной кривой.
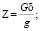
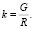
Среднеинтегральное тяговое усилие на прямолинейном в профиле участке при условии аппроксимации тягового усилия в заданном диапазоне зависимостью FT = А – Вυ2 определяется по формуле
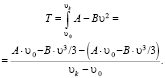(9)
На прямолинейных в профиле участках пройденное расстояние определяется зависимостью (7) или по формуле:
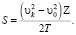(10)
Таким образом, получены зависимости для решения прямой и обратной задачи тяговых расчетов.
При известном среднеинтегральном значении Т на прямолинейном в профиле участке:
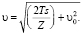(11)
На участках вертикальных кривых:
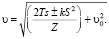(12)
Так как, на первом этапе расчета, при определении скорости на вертикальной кривой до определения конечной скорости движения среднеинтегральное тяговое усилие в диапазоне скоростей υ0 – υк определить невозможно, задача решается в два этапа. Вначале по формуле (11) или (12) определяется скорость движения в конце участка при заданном тяговом усилии в начале участка и равномерном ускорении. Затем в диапазоне скоростей υ0 – υк определяется среднеинтегральное тяговое усилие по формуле (9). После этого по формулам (11) или (12) значение скорости уточняется с учетом величины среднеинтегрального значения Т и среднеинтегрального ускорения.
При расчетах по формуле (2) и (3) и по формулам (11) и (12) с использованием предлагаемой методики получены одинаковые результаты.
Для определения времени движения на прямолинейных в профиле участках ранее была выведена зависимость [1]:
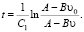(13)
В этом случае тяговое усилие с учетом сопротивления аппроксимируется линейной зависимостью, а не двучленным полиномом A – Bυ2, что приведет к снижению точности расчетов.
С целью повышения точности расчетов получено решение дифференциального уравнения в виде
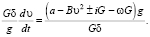(14)
Для повышения точности расчетов при определении времени движения в уравнении (14) целесообразно вместо правой его части принять среднеинтегральное значение T, полученное при определении скорости движения по формулам (9), (11), (12).
На прямолинейном в профиле участке:
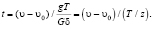(15)
На участках вертикальных кривых при расчетах t необходимо учитывать изменение сопротивления движению при непрерывных изменениях уклона на вертикальной кривой.
С учетом того, что среднеинтегральное значение изменения тягового усилия на участке длиной S при радиусе вертикальной кривой R (м) определяется по формуле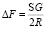 
, дифференциальное уравнение движения на вертикальной кривой имеет вид
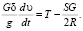(16)
Расчетная зависимость для определения времени на вертикальной кривой:
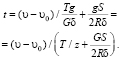(17)
Следует отметить, что при известном среднеинтегральном тяговом усилии T можно определить время движения на участке вертикальной кривой, используя зависимость для решения дифференциального уравнения в виде
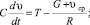(18)
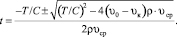(19)
где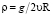 
, остальные обозначения те же, что и в формулах (7)–(9).
Если скорость движения определена с использованием зависимостей (1), (2), то определение времени движения на участке упрощается. Среднеинтегральное ускорение в этом случае определяется по формуле
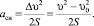(20)
где υ0 – скорость в начале движения на участке, м/сек; υ – скорость движения в конце участка.
Время движения определяется по формуле
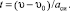(21)
На вертикальных кривых, на определенном расстоянии от начала движения скорости движения автотранспортных систем достигают экстремального значения – υэ (максимальное значение скорости при разгоне автопоезда в начале движения и минимальное при снижении скорости на вертикальной выпуклой кривой). В точке экстремума скорости вектор изменения скорости меняется на противоположный.
Расстояние до точки экстремума:
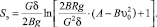(22)
Значения ρ в зависимости от S приведены в таблицах приложения [1], а также могут быть рассчитаны по формуле, полученной в результате преобразования зависимости (3):
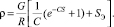(23)
В формулах (22), (23): Sэ – расстояние до точки экстремума, м;
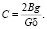(24)
Так как в точке экстремума тяговое усилие, определяемое по формуле A – Bυ2, равно 0, то скорость в любой точке, находящейся на расстоянии Sэ от точки экстремума, определяется по формуле
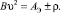(25)
Формула (25) получена путем преобразования зависимости (2), исходя из того, что в точке экстремума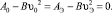 
При определении скорости движения на вертикальных выпуклых кривых ρ применяются со знаком «+», на вогнутых – со знаком «-».
Определив скорость в точке экстремума, легко определить скорость при движении в любой точке на вертикальной кривой с тем же начальным уклоном по зависимости
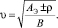(26)
где Аэ – тяговое усилие в точке экстремума; υ – скорость в конце вертикальной кривой, м/с.
С использованием зависимостей (23), (26) легко определить скорость движения на любом расстоянии до точки экстремума, что значительно ускоряет построение уточненного графика движения лесовозных автопоездов. Для решения обратной задачи – определения расстояния пройденного автопоездом при изменении скорости от υ0 до υк – находится ρ по формуле (25).
При решении этих задач следует иметь в виду, что решение их указанным способом возможно лишь при наличии экстремальных значений скорости при заданных условиях.
Заключение
В работе обоснованы и выведены зависимости и определена методика расчетов показателей движения лесовозных автопоездов при неустановившемся и установившемся режимах движения. Разработанные методы расчетов учитывают все основные факторы, влияющие на показатели движения, и обладают большей точностью и достоверностью, чем традиционные методы, зачастую применяемые на лесотранспорте.
Выведенные зависимости и обоснованные методы позволяют решать широкий круг технико-экономических и инженерных задач при проектировании, планировании и эксплуатации лесотранспорта. В частности, приведенные зависимости можно использовать для определения скорости и времени движения лесовозных автопоездов в различных режимах движения и, как следствие, расчета их производительности и технико-экономических показателей при работе в различных природно-производственных условиях, а также для обоснования оптимального типа автопоезда при работе в конкретных условиях эксплуатации и его режимов работы.