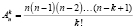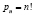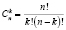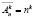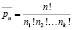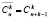При кратком изложении математических курсов особо остро встаёт проблема выбора учебного материала, при котором необходимо по возможности максимально полно представить предмет, описать основные задачи и ознакомить с важнейшими методами. При этом вопросы методологии, согласованности лекционного материала и практических занятий, визуализации материала, организации самостоятельной работы играют важнейшую роль. Ибо, как хорошо известно, способный и увлеченный предметом студент даже из плохой лекции может взять многое, что нельзя сказать о студенте, имеющем посредственные базовые знания по школьной программе [1]. Значительные трудности испытывают и студенты, теряющиеся в выборе подходящей дополнительной литературы, которая в значительной степени отражает вкусы и интересы авторов книг и разбросана по многочисленным источникам.
Целью настоящей статьи является: проектирование содержания вводного курса дискретной математики втуза с небольшим количеством учебных часов, включающего элементы комбинаторики, производящих функций и рекуррентных соотношений; оценка возможностей реализации такой программы за 6–8 часов лекций, а также разработка методических рекомендаций по обучению студентов решению ряда важнейших задач комбинаторики и рекуррентных уравнений.
Содержание курса и методические рекомендации по обучению решению задач
Приведем перечень вопросов, наиболее важных для первого знакомства с комбинаторикой. Это: задачи комбинаторного анализа; принципы сложения, умножения и клеток; формулы для подсчета основных комбинаторных конфигураций; бином Ньютона и его обобщение, свойства биномиальных коэффициентов; мощность булеана; рекуррентные формулы, соотношения и уравнения; производящие функции и их применение в комбинаторике и решении рекуррентных уравнений; последовательности Фибоначчи и Каталана.
Важнейшие формулы комбинаторики и некоторые типовые задачи
Для начала обсудим некоторые аспекты преподавания основ комбинаторики и рассмотрим типовые примеры. В комбинаторике, как уже отмечалось, примерам отводится особая роль. Часто на языке примеров проводятся доказательства (особенно это характерно для программ с малым количеством учебных часов). Наш курс начинается с введения в предмет, формулировок фундаментальных принципов умножения и сложения, а также вывода формул подсчета основных комбинаторных конфигураций (таблица). Подчеркнем, что все формулы таблицы доказываются с применением принципа умножения и обычно представляются соответствующими теоремами.
|
Размещения без повторений и с повторениями |
Перестановки без повторений и с повторениями |
Сочетания без повторений и с повторениями |
|
|
|
|
|
|
|
|
Среди формул таблицы нетривиальными являются две последние. Их логическое обоснование может быть связано со следующими задачами.
Задача 1 (сочетания с повторениями). В киоске продаются белые, красные и желтые розы. Сколько различных по составу букетов из 7 роз можно составить? Алгоритм решения этой задачи следующий. Действительно, пусть в некотором букете 3 белые розы. Тогда запишем 111 и поставим 0. Если в букете 2 красные розы запишем далее 11 и поставим 0. Если в букете еще 2 желтые розы, напишем 11. Таким образом, получим девятибитовое слово с семью единицами и двумя нулями. Ясно также, что и любому двоичному слову длины 9 с двумя нулями можно поставить в соответствие букет из 7 роз трех цветов. Так, например, слову 001111111 будет отвечать букет только из желтых роз, слову 011111110 – только из красных, слову 111001111 – из 3 белых и 4 желтых и т.д. Таким образом, устанавливается биекция (взаимно однозначное соответствие) между букетами роз разного состава и девятью битовыми словами с двумя нулями. Теперь вопрос, поставленный в задаче, можно переформулировать. Сколькими способами можно установить два 0 в табло из 9 битов? Ответ: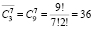 
.
Здесь следует обратить внимание на принцип параллельного моделирования. Букет из роз мы заместили новым объектом – двоичным словом. Тем самым мы редуцировали задачу к изученной (что такое число сочетаний без повторений, студент уже знает). Такой принцип часто используется в комбинаторике и является эффективным инструментом решения задач. С рассмотренной задачей методологически тесно связана следующая задача – о количестве решений алгебраического уравнения.
Задача 2. Сколько целочисленных неотрицательных решений имеет алгебраическое уравнение x + y + z = 7? На первый взгляд, эта задача далека от предыдущей, но, по сути, есть эквивалентная формулировка предыдущей, однако учащиеся это не всегда отмечают. Здесь полезно выдать задание на самостоятельную работу, чтобы студенты перечислили все 36 решений уравнения. Выполняя это задание, обучаемые лучше прочувствуют постановку вопроса.
После разбора этих задач естественно перейти к общей формуле для подсчета числа сочетаний с повторениями и привести ее в виде теоремы: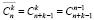 
.
При этом пояснительные замечания будут здесь минимальными.
Задача 3 (перестановки с повторениями). Имеется набор букв: «Р», «Н», три буквы «А» и две буквы «Б». Если этим буквам придать некоторый порядок – получим перестановку. Например, слово «БАРАБАН». Меняя любые буквы между собой, получим другую перестановку. Если бы все буквы были различны, то всего перестановок было бы p7 = 7! = 5040. Но в нашем случае, очевидно, что, переставляя между собой одинаковые буквы, мы не приходим к новым словам – новым перестановкам. Учитывая сказанное и используя правило умножения, заключаем, что различных по прочтению перестановок будет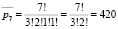 
. Обратим внимание, что существует много вариаций этой задачи: расстановка книг на полке, среди которых есть одинаковые; расстановка шаров разных цветов на желобе и т.д.
Обобщая эту задачу, приходим к теореме о числе перестановок с повторениями: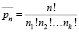 
, (n1 + n2 + ... + nk = n). Комментарии будут здесь также минимальными.
Задача 4 (о размещении предметов). Начнем с хорошо известного примера – игры в домино. Имеется 28 костей. Каждый из 4 игроков случайным образом выбирает 7 костей. Сколько существует раскладов? Предварительно зададимся вопросом: так ли важно, что кости разбираются одновременно? Нет. Поэтому будем считать, что сначала берет первый, затем второй, третий и, наконец, четвертый игрок. Такая детализация последовательности действий означает, что мы опять свели задачу к применению принципа умножения, согласно которому будем иметь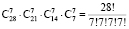 
раскладов.
Далее напрашивается естественное обобщение этой задачи. Пусть имеется k одинаковых коробок и n различимых между собой предметов. В первую коробку необходимо положить n1 предмет, во вторую n2 и т.д., в последнюю nk предметов; n1 + n2 + ... + nk = n. Сколькими способами это можно сделать? Ответ содержится в теореме:
.
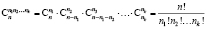Важное место в комбинаторике занимают следующие два утверждения.
Теорема 1 (биномиальная).
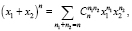
где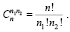 
Теорема 2 (полиномиальная).
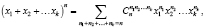
где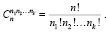 
Коэффициенты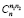 
и 
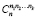– называются соответственно биномиальными и полиномиальными коэффициентами (заметим, что первый есть частный случай второго). Среди многочисленных следствий из теоремы 1 отметим здесь только одно 
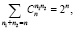по существу являющееся доказательством теоремы о мощности булеана. Другие следствия мы здесь не приводим [2]. Доказательства теорем 1 и 2 необходимо провести обязательно, так как методология этих рассуждений будет использована далее при построении производящих функций.
Следующий пример чисто конструктивный, но полезный с точки зрения закрепления полиномиальной формулы.
Пример 1. Найти коэффициент при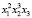 
в разложении 
.
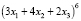Так как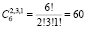 
, то коэффициент при 
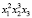равен 60•3243•2 = 69120.
Производящие функции в комбинаторике
Производящие функции играют важную роль во многих разделах математики, имеют широкие приложения и являются незаменимым аппаратом комбинаторики. Полагая, что читатель знаком с определением производящей функции числовой последовательности, напомним только лишь формулы
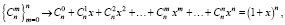
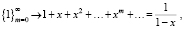
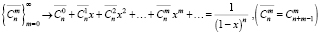
и рассмотрим ряд типовых задач, а затем приведем дополнительный комментарий.
Задача 5. Пусть A = {a, b, c, d, e} – множество, (1, 2, 3, 2, 1) – вектор спецификаций. Сколько сочетаний по 3 с повторениями можно составить из элементов множества A с учетом заданных спецификаций? Для ответа на вопрос составляется производящая функция (здесь предварительно необходимо вспомнить формулу бинома Ньютона)
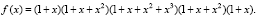(1)
После раскрытия скобок в (1) получим 144 слагаемых (уместен вопрос «почему их 144»?), каждое из которых отвечает определенной выборке. Например, если взять 1 из первой скобки, x – из второй, x3 – из третьей, x2 – из четвертой и x – из пятой, то произведение x7 отвечает выборке: bcccdde. После приведения подобных, получим
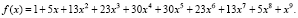
Коэффициент при x3 равен 23 и дает число сочетаний с повторениями. Среди них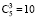 
сочетаний без повторений и 13 с повторениями: abc, abd, abe, bcd, bce, acd, ade, bde, cde, ace, dda, ddb, ddc, dde, bba, bbc, bbd, bbe, cca, ccb, ccd, cce, ccc.
Обратим внимание, что f(x) выступает в роли «хранителя» комбинаторных чисел, а его коэффициенты позволяют ответить и на другие вопросы в рамках данной задачи. Заметим, что производящей функцией для этой задачи без вектора спецификаций будет
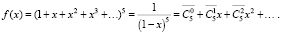
Можно сказать, что вектор спецификаций имеет символический вид (?, ?, ?, ?, ?).
Задача 6 (игра в кости). Пусть подбрасывается k игральных костей. Рассматривается величина n – сумма выпавших очков. Анализируя задачу 5, нетрудно сообразить, что производящей функцией числа вариантов, дающих в сумме n очков, будет
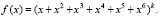(2)
Раскрывая произведение в (2), получим многочлен степени 6k. Коэффициент при xn (k ? n ? 6k) даст в точности ответ на поставленный вопрос.
Задача 7 (размен денег). Построить производящую функцию для определения числа способов размена n рублей через монеты в 1, 2, 5 и 10 рублей. Учитывая, что монеты четырёх достоинств, а параметр n не конкретизирован, то производящая функция будет иметь четыре сомножителя, каждый из которых имеет вид бесконечной геометрической прогрессии, со знаменателями x, x2, x5 и x10 соответственно:
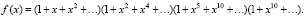(3)
После раскрытия скобок в (3) коэффициент при xn даcт ответ. О применении производящих функций к комбинаторным подсчетам можно прочитать в книгах [2; 3]. В завершение выскажем основной принцип решения таких задач. На первом шаге, исходя из анализа условий задачи, строится функция f(x), моделирующая процесс выбора сочетаний. На втором шаге функция f(x) «распаковывается», т.е. раскладывается по степеням x. В результате чего определяются комбинаторные числа, как коэффициенты при степенях x.
Производящие функции и линейные рекуррентные уравнения
Производящие функции дают эффективный метод решения линейных рекуррентных уравнений с постоянными коэффициентами k-го порядка
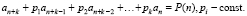(4)
При этом считается, что числа a0, a1,…,ak-1 (начальные условия) – заданы. Пусть для начала P(n) = 0 (случай однородного уравнения). Идея метода заключается в следующем. Вводится производящая функция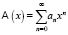 
с неизвестными коэффициентами 
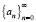. Затем уравнения (4) умножаются на xn+k и суммируются. В результате бесконечная система уравнений приводится к виду функции
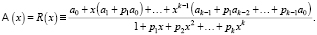
Так как R(x) – правильная рациональная функция, то ее раскладывают в ряд по степеням x, но A(x) – тоже ряд. Приравнивая соответствующие коэффициенты в равенстве A(x) = R(x), находят явный вид коэффициентов an = a(n).
Пример 2. Рассмотрим уравнение 2-го порядка с начальными условиями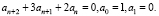 
Тогда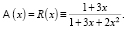 
Разлагая функцию R(x) в ряд, получаем
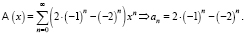
Если P(n) – многочлен, то уравнение (4) сводится к однородному уравнению более высокого порядка [3].
Иной метод решения линейных рекуррентных уравнений с постоянными коэффициентами приведен в статье [4], там же изложена и общая теория таких уравнений.
Нелинейные уравнения и числа Каталана
Хорошо известно, в частности программистам, понятие правильных скобочных форм [3; 5]. Вот примеры таких форм:
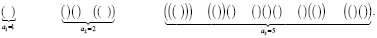
Рассмотрим теперь нелинейное рекуррентное соотношение
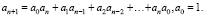(5)
Последовательные вычисления дают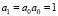 
, 
,
, 
, 
, 
, 
, …
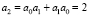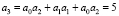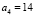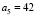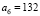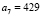На соотношение (5) будем смотреть как на бесконечную систему уравнений относительно величин an. Числа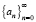 
, удовлетворяющие соотношениям (5), т.е. представляющие собой решение уравнений (5), называются числами Каталана. В частности, они описывают число правильных скобочных форм. Для нахождения общего члена an = a(n) последовательности 
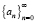используют также производящую функцию
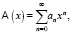
которая, как несложно показать, должна удовлетворять иррациональному уравнению
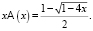(6)
Левая часть формулы (6) представляет собой формальный ряд. Разлагая правую часть в ряд и приравнивая коэффициенты при одинаковых степенях x, находим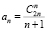 
.
Замечание. Отметим, что исходный объект (5) является дискретным – рекуррентно заданной числовой последовательностью. После некоторой трансформации (как говорят, «упаковки»), рождается непрерывная функция A(x) – «хранитель» дискретной информации. Разложение A(x) в ряд позволяет определить снова дискретный объект – общий член числовой последовательности (рисунок). Заметим, что в отличие от R(x) – производящей функции линейного рекуррентного уравнения, в этом примере она иррациональна. Кроме того, ряд Каталана оказывается сходящимся в области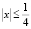 
.
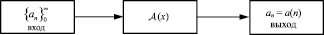
Схема метода производящих функций
Замечание. К сожалению, нелинейных уравнений, допускающих столь простое и красивое решение, насчитывается немного, а этот пример демонстрирует скорее исключение, чем правило. Рассмотрим теперь нелинейное уравнение первого порядка
an+1 = pan (1 – an),
где p?(1,4) – const (параметр).
Оно имеет два простых решения an = 0 и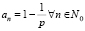 
. Других решений этого уравнения, представимых какими-либо формулами, мы не знаем. Однако много интересных свойств решений этого уравнения установить удалось, но методами совсем далекими от производящих функций.
Заключение
В настоящее время имеется много хороших книг и учебных пособий по дискретной математике. Лектору остается вроде бы совсем немного: отобрать нужный материал и погрузить его в заданный объем часов. Однако этого оказывается мало, так как материал еще нужно переработать, чтобы он был усвоен студентами, учитывая их уровень подготовки, а последний, как известно, из года в год не растет. Описанный план изложения комбинаторики неоднократно был апробирован, имеет положительный опыт в ряде вузов с небольшим объемом учебных часов по программе и, на наш взгляд, формирует необходимую базу для дальнейшего, возможно самостоятельного, изучения комбинаторики. Затронутая в статье тема многогранна, а высказанные методические рекомендации по поводу решения примеров приведены очень кратко. Кроме того, многие аспекты теории и важные примеры нам обсудить не удалось. Поэтому начатый здесь разговор планируется продолжить в следующих публикациях.
Из года в год обращает на себя внимание следующий факт. Большая часть студентов, ранее испытывающих трудности при изучении высшей математики, при изучении дискретной математики, в данном случае комбинаторики, приобретают, если так можно сказать, «интеллектуальное вдохновение», что явно сказывается в их поведении, самооценке и результатах контрольных опросов. Конечно, это в значительной степени связано с тем, что материал вводного курса ДМ не требует знаний из смежных разделов высшей математики. Однако это подчеркивает и особенности восприятия человеком разного рода информации и его мышления в целом. Что касается работ, посвященных методике изложения тем дискретной математики, то их множество. Для этого достаточно обратиться, например, к списку литературы, приведенному в [6].