В современных системах контроля качества информационных процессов используется традиционный параметрический подход, который предусматривает анализ определенных параметров [1]. На этапе контроля делается вывод о пригодности информационного объекта к выполнению своих функций в рамках обеспечения деятельности общей информационной системы (ОИС). На этапе диагностирования определяется область и величина отклонения параметров исследуемого объекта (подсистемы) от номинальных значений, то есть наличие и виды дефектов, которые, в свою очередь, могут оказывать влияние на безопасность всей системы в целом [2].
Современные технологии диагностирования предусматривают использование комплексных показателей качества при многопараметрическом анализе, однако они не обладают наглядностью и требуют значительных затрат в практической реализации [3, 4].
Цель исследования: разработка модели безопасности информационных систем, обеспечивающей определение взаимного влияния сигналов, представленных в виде геометрических фигур, на основе анализа их геометрического взаимодействия в многомерном метрическом пространстве.
Под безопасностью ИС понимается защищенность системы, т.е. ее способность противостоять различным воздействиям [5]. Безопасностью информационной системы можно считать обнаружение негативного влияния посторонних сигналов (помех) на полезные информационные сигналы, вызывающих искажение или потерю информации полезных сигналов. Защита информации – это комплекс мероприятий, направленных на обеспечение информационной безопасности. Для обеспечения защиты информации необходимо определить показатель, который будет определять степень различных негативных воздействий на информационные сигналы информационной системы.
Предлагается в качестве комплексных показателей безопасности информационной системы использовать как геометрические объемные фигуры, так и их геометрическое взаимодействие [6, 7].
Проводя анализ взаимодействия геометрических фигур по изменению их координат в виртуальном пространстве, можно выделять обобщенную характеристику их различия (похожести) и степени их взаимодействия по удаленности фигур друг от друга [7].
Сферическими координатами называют систему координат для отображения геометрических свойств фигуры в трех измерениях, посредством задания трех координат (r, θ, λ), где r – расстояние от начала координат, θ – зенитный угол или полярное расстояние, которое иногда называют коширотой, λ – азимутальный угол или долгота, причем θ изменяется от 0° до 180°, а λ изменяется от 0° до 360° [8].
x = r sin θ cos λ; (1)
y = r sin θ sin λ; (2)
z = r cos θ. (3)
Система уравнений представляет преобразование между сферической и декартовой системами координат [8]. Следовательно, функции f1 , f2 , f3 равны
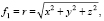 (4)
(4)
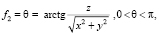 (5)
(5)
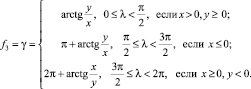 (6)
(6)
Расстояние между точками А (x1, y1) и B (x2, y2) в декартовой системе координат вычисляется по формуле
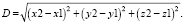 (7)
(7)
Если представить значения координат точек А и В как центры сфер, a r1 и r2 как радиусы сфер в пространстве, то расстояния между сферами в пространстве будут вычисляться по формуле
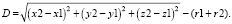 (8)
(8)
Передатчик обеспечивает передачу сигнала в среду распространения в заданном секторе пространства, путем создания электромагнитного поля или электрического тока, которые будут регистрироваться приемником. Данная среда характеризуется набором физических параметров, которые определяют необходимые условия передачи информационного сигнала.
Наиболее уязвимыми участками канала передачи данных являются: источник сигнала, среда передачи и приемник. Широкое распространение получила QAM – (Quadrature Amplitude Modulation – модуляция методом квадратичных амплитуд) т.е. цифровой информационный поток передается в виде аналогового сигнала [9]. Данный метод осуществляется путем разделения несущей волны на две несущие одинаковой частоты, сдвинутые относительно друг друга на 900, каждая из которых промодулирована по одному из двух или более дискретных уровней амплитуды. Комбинация всех уровней, в свою очередь, представляет собой бинарную битовую картину. Уровень QAM определяется в соответствии с точкой диаграммы канстелляции амплитудой, циклической частотой и начальной фазой гармонического колебания. Точка диаграммы канстелляции характеризует байт передаваемой цифровой последовательности. Поэтому для создания модели безопасности информационных систем правомерно использовать тривиальные уравнения гармонических колебаний.
Уравнение гармонического колебания имеет вид
S(t) = A cos(ωt + φ), (9)
где S – отклонение колеблющейся величины в текущий момент времени t от среднего за период значения; А – амплитуда колебания; ω – циклическая частота; φ – начальная фаза колебаний.
Имеются 2 гармонических колебательных процесса, описываемых выражениями
S1(t) = A1cos(ω1t + φ1), (10)
S2(t) = A2cos(ω2t + φ2). (11)
В выражениях (1), (2), (3) если выразить радиус сферы r как значение амплитуды колебания А; θ – зенитный угол, как значение ω – циклической частоты; λ – азимутальный угол, как значение φ – начальной фазы колебания, то получим выражения
x = r sin ω cos φ; (12)
y = r sin ω sin φ; (13)
z = r cos ω. (14)
Подставим выражения (12), (13), (14) в выражение (8) и после несложных математических преобразований получим модель для определения расстояний f(x01, y01) между гармоническими колебаниями S1(t) и S2(t):
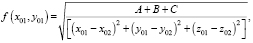 (15)
(15)
где
А – 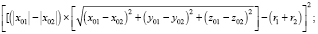
В – 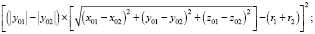
C – 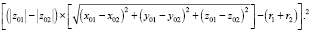
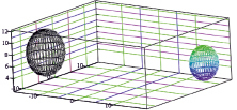
На рис. 1, а, б, представлены сигналы, размещенные в декартовых системах координат, причем сами сигналы представлены в виде сфер, построенных в сферических системах координат. На рисунках видно, что при изменении параметров сигналов (амплитуда, частота и фаза), геометрическое расстояние в виртуальном пространстве между сигналами изменяется.
 а)
а)  б)
б)
Рис. 1. Изометрическое представление сигналов в виде сфер в декартовых системах координат
Анализ рисунков позволяет сделать вывод, что при различных частотах, амплитудах и начальных фазах различных сигналов, геометрическое расстояние между сигналами может быть равным 0 (рис. 1, а).
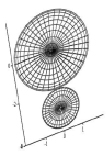
Если использовать традиционный параметрический подход, то результат негативного воздействия на полезный сигнал других сигналов или помех может быть ложным. И достоверность такой оценки низка. Это обусловлено анализом каждого параметра в отдельности (рис. 2, а, б, в).
Рис. 2, в, наглядно показывает, что в виртуальном пространстве сигналы якобы взаимно влияют друг на друга, если анализ проводить по одному из параметров сигнала, однако рис. 2, а, и 2, б, показывают, что взаимное влияние отсутствует.
Пример взаимного влияния сигналов по двум параметрам представлен на рис. 3, а, б, в.
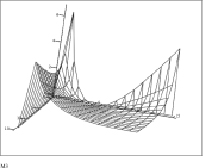
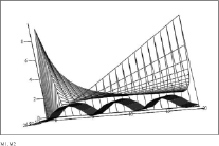
Результат исследования заключается в том, что при использовании полученной модели (15) обнаруживается эффект, когда различные передатчики, работающие на различных частотах, способны оказывать взаимное негативное влияние друг на друга при определенном значении их амплитуд и начальных фаз при использовании QAM, искажая содержащуюся в них информацию. На рис. 4, а, б, представлены графики положений двух различных сигналов в виртуальном пространстве декартовых координат при изменении амплитуд, начальных фаз и частот (в соответствии с правой частью уравнения (15)), выраженных в сферических координатах. На графике (рис. 5, а) проведено совмещение виртуальных декартовых координат исследуемых сигналов, «расстояния» f(x01, y01) (15) между которыми больше нуля. Графики не пересекаются, таким образом, взаимное влияние сигналы друг на друга не оказывают. Анализ графика (рис. 5, б) показывает, что при определенных отношениях частот, амплитуд и фаз сигналов «расстояния» f(x01, y01) (15) между сигналами в виртуальном пространстве сокращаются, в отдельных точках сигналы явно пересекаются, то есть оказывают негативное влияние друг на друга.
 а)
а) 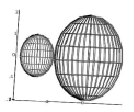 б)
б) 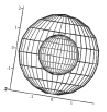 в)
в)
Рис. 2. Представление сигналов в виде сфер в декартовых системах координат при исключении одного из параметров сигнала
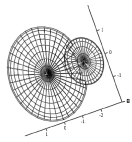 а)
а) 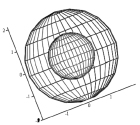 б)
б) 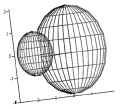 в)
в)
Рис. 3. Пример взаимного влияния сигналов по двум параметрам
 а)
а) 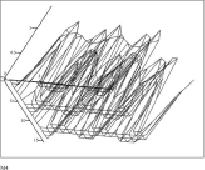 б)
б)
Рис. 4. Графики координат различных сигналов в виртуальном параметрическом пространстве
 а)
а) 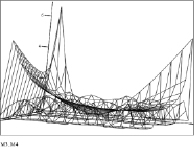 б)
б)
Рис. 5. Графики взаимного влияния различных сигналов в виртуальном параметрическом пространстве
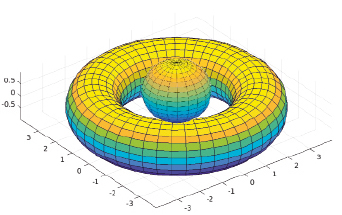
Рис. 6. Графическая модель различных сигналов, представленных в виде тора и сферы, обеспечивающих многомерное параметрическое уплотнение
Графически представив виртуальные координаты взаимодействия сигналов информационных систем, с учетом условного перевода сферических координат в параметры системы, можно проводить исследования по обнаружению причин искажений и потери информации после демодуляции сигналов передатчиков, работающих на разных частотах. Причем искажения этих сигналов будут обусловлены амплитудами и начальными фазами элементов диаграмм канстелляции QAM.
Научным выводом проведенных исследований является: передача информации на различных несущих частотах не исключает взаимного негативного влияния сигналов друг на друга при использовании QAM. И в то же время на одинаковых несущих частотах при определенных значениях фаз и амплитуд различных сигналов, использующих различные диаграммы канстелляции QAM, можно передавать различную информацию, обеспечивая расширение частотного ресурса. Данная возможность дает повод для определения нового вида уплотнения передаваемой информации и повышения скрытности передаваемых сигналов, которое можно назвать многомерным параметрическим уплотнением (рис. 6).
Таким образом, для наглядного представления меры «близости» между процессами, ввиду многопараметрической оценки качества функционирования систем при трехмерном наглядном графическом представлении очень сложно представить многомерные процессы в декартовых системах координат. Необходимо переходить в область многомерных метрических пространств. То есть совмещать различные координаты параметрических пространств в виртуальные координаты исследуемых многомерных пространств. Таким образом, данное исследование дает возможность математически проследить последовательность «совмещений» трехмерных параметрических пространств в декартовых системах координат в многомерные пространства. Как следствие, можно определять влияние друг на друга сигналов различных информационных систем для выработки комплекса мероприятий по защите информации.



