Одним из параметров классического алгоритма бактериальной оптимизации (Bacterial Foraging Optimization, BFO) [1, 2] является так называемый шаг хемотаксиса – величины, на которую бактерия сдвигается в направлении своего движения при каждой итерации алгоритма. Значение этого параметра достаточно сильно влияет на близость найденного решения к оптимальному, а его неизменность (в классическом алгоритме) приводит к плохой сходимости, когда бактерии, даже обнаружив глобальный оптимум, начинают роиться вокруг него, без возможности улучшить решение. Фактически, при поиске оптимума дифференцируемых функций, проблема выбора шага хемотаксиса аналогична проблеме выбора шага для хорошо известного и классического алгоритма градиентного спуска, когда большой постоянный шаг может приводить к плохой сходимости, а малый шаг – к слишком большим временным затратам или невозможности выйти из локального минимума.
В некоторых работах, например в [3], предпринимается попытка автоматической адаптации величины шага для каждой отдельной бактерии, однако, во-первых, для такой адаптации авторы требуют, чтобы оптимизируемая функция была унимодальной, а во-вторых, в предложенном подходе неявно считается, что мы заранее знаем оптимальное значение оптимизируемой функции и неизвестно только его положение в пространстве поиска, что в условиях реальных оптимизационных задач бывает далеко не всегда.
В ряде других работ предпринимаются попытки создать гибридные алгоритмы, совмещающие в себе различные комбинации стохастических алгоритмов [4] или сочетание стохастического алгоритма с детерминированным [5].
Целью настоящей работы является сравнительная оценка способов корректировки шага хемотаксиса на основе анализа результатов вычислительного эксперимента.
В настоящей работе предлагаются два подхода к автоматической корректировке шага хемотаксиса в процессе работы алгоритма: детерминированный и стохастический. Оба подхода не требуют априорных знаний о поведении оптимизируемой функции и могут применяться как отдельно, так и в совместной комбинации, как это будет показано ниже.
Детерминированный подход: уменьшение начальной величины шага экспоненциальной функцией
Первый из предлагаемых подходов к автоматической корректировке шага хемотаксиса заключается в уменьшении исходного значения шага пропорционально проведенным итерациям (рис. 1). При таком подходе расстояние, на которое каждая отдельная бактерия передвигается в ходе хемотаксиса, рассчитывается по формуле
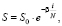 (1)
(1)
где S – длина фактического шага; S0 – длина начального шага (один из исходных параметров алгоритма); β – параметр, определяющий скорость уменьшения шага в зависимости от итерации алгоритма), i – номер текущей итерации алгоритма, N – максимальное число итераций алгоритма.
Очевидно, что при значении параметра β, равного нулю, формула (1) вырождается в канонический алгоритм бактериальной оптимизации с постоянным шагом.
Идеей такой модификации служит тот факт, что, позволяя бактериям в начале процедуры поиска оптимума исследовать большее пространство за счет большего шага, мы затем искусственно снижаем их подвижность, заставляя все более подробно исследовать области ранее обнаруженных оптимумов.
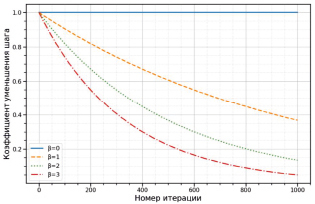
Рис. 1. Коэффициент уменьшения шага хемотаксиса в зависимости от параметра β в (1)
Результаты применения описываемой модификации можно видеть на рис. 2. Хорошо видно, что значение β = 2 позволяет обеспечить практически такой же уровень точности решения даже при увеличении начального шага в 5 раз (с 0,1 до 0,5).
Стохастический подход: случайный выбор величины шага
Второй из предлагаемых подходов заключается в выборе шага хемотаксиса для каждой бактерии случайным образом в интервале от нуля до значения, соответствующего параметру алгоритма S0. Для этого в формулу расчета шага вносится в виде множителя некоторая случайная величина X∈[0, 1], распределенная по какому-либо закону.
S = S0•X. (2)
В основе данного подхода лежит предложение рассматривать шаг хемотаксиса S0, заданный как параметр алгоритма, не как обязательную величину, на которую бактерия обязана сдвинуться в пространстве поиска на каждой итерации, а как ее (бактерии) потенциальную возможность сдвинуться на указанное расстояние, которой она, тем не менее, может воспользоваться не полностью.
При проведении численных экспериментов, кроме того, было сделано предположение, что не только случайность будет иметь влияние, но и закон распределения случайной величины также будет оказывать влияние на точность получаемых решений, поэтому в численных экспериментах были использованы следующие, широко известные, законы распределения случайной величины:
– равномерное распределение;
– нормальное распределение с параметрами μ = 0,5 и σ = 0,25 (более равномерное распределение случайных чисел по интервалу (рис. 3, верхний левый график));
– нормальное распределение с параметрами μ = 0,5 и σ = 0,167 (более выраженная концентрация случайных чисел в середине интервала (рис. 3, верхний правый график));
– бета-распределение с параметрами α = 2 и β = 1 (рис. 3, нижний левый график);
– бета-распределение с параметрами α = 1 и β = 2 (рис. 3, нижний правый график).
Полученные результаты приведены ниже на рис. 4. Хорошо видно, что использование в ходе хемотаксиса формулы (2) с любым законом распределения из рассмотренных дает всегда лучшие результаты по сравнению с шагом постоянной величины. В то же время различные законы распределения существенно влияют на получаемый результат и самые точные решения получаются при использовании бета-распределения с параметрами α = 1 и β = 2 (рис. 3, нижний правый график).
Сочетание предложенных подходов
Поскольку оба описанных выше подхода заключаются в простом добавлении множителя в формулу расчета текущего шага бактерии, они могут без потери эффективности применяться совместно, до некоторой степени усиливая друг друга:
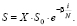 (3)
(3)
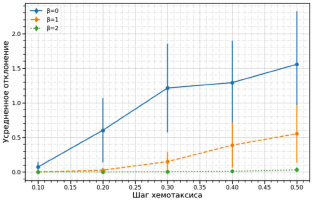
Рис. 2. Усредненное отклонение от оптимума и среднеквадратичное отклонение при различных значениях параметра β
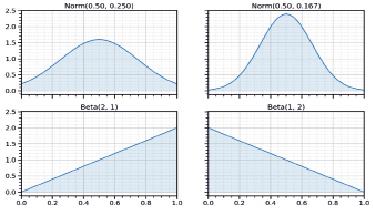
Рис. 3. Плотности вероятностей случайных множителей для шага хемотаксиса
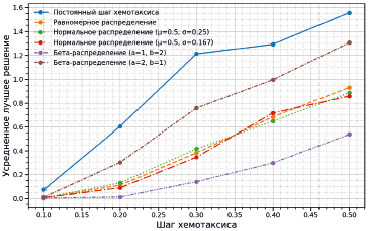
Рис. 4. Влияние закона распределения случайной величины шага на точность решения
Результаты численных экспериментов при совместном использовании подходов случайного шага и его экспоненциального уменьшения в ходе итераций приведены на рис. 5. Так же как и в предыдущем случае, любой закон распределения дает гарантированно лучшие результаты по сравнению с шагом постоянной величины, а бета-распределение с параметрами α = 1 и β = 2 также оказывается лучшим из всех протестированных.
Условия проведения численных экспериментов
Вычислительный эксперимент проводился на компьютере в следующей конфигурации: процессор – Intel Core i5-2500K (базовая частота 3.30 ГГц); оперативная память – 8 Гб (1333 МГц); операционная система – Microsoft Windows 10 Education версия 10.0.18363).
Программная среда тестирования алгоритмов и сами алгоритмы были реализованы на языке программирования C# (среда исполнения Microsoft .NET Framework 4.7.2, режим компиляции Release с включенной оптимизацией генерируемого кода) в среде разработки Microsoft Visual Studio Community 2019.
Проверка эффективности предложенных подходов адаптации шага хемотаксиса проводилась путем численных экспериментов по нахождению оптимума функций Растригина [2] на интервале x1, x2∈[–5.12, 5.12]. Популяция бактериальной колонии во всех экспериментах составляла 1000 особей (бактерий). Для каждой колонии выполнялось 1000 итераций алгоритма. Каждый численный эксперимент по оптимизации повторялся 100 раз при неизменных исходных параметрах, после чего вычислялись среднее значение лучших решений в каждом повторе и величина стандартного отклонения. В целях ускорения расчетов эксперименты проводились параллельно в режиме один эксперимент на одно физическое ядро процессора (технология hyper-threading на процессоре не применялась). Вычислительное время, потраченное на оптимизацию, в задачи исследований не входило.
Заключение
1. В работе тестировались три подхода к автоматической корректировке шага хемотаксиса в процессе работы алгоритма бактериальной оптимизации: детерминированный, стохастический, а также их комбинация. Все протестированные подходы не требуют априорных знаний об оптимизируемой функции. Детерминированный и стохастический подходы могут применяться как отдельно, так и в совместной комбинации.
2. При проведении вычислительного эксперимента, направленного на оценку сходимости анализируемых подходов, в качестве пространства поиска использовалась двумерная функция Растригина на интервале [–5.12, 5.12].
3. Моделирование процесса бактериальной оптимизации, с заданными параметрами изменения шага хемотаксиса, заключалось в реализации двух основных этапов: случайной генерации 1000 особей, образующих колонию, и выполнении 1000 итераций алгоритма оптимизации. Каждый набор параметров изменения шага хемотаксиса тестировался 100 раз, путём запуска процесса бактериальной оптимизации с соответствующими параметрами. Результаты выполнения каждого процесса сохранялись, а затем усреднялись. Полученные усреднённые результаты были отображены на рис. 1–5.
4. Детерминированный подход к автоматической корректировке шага хемотаксиса заключается в уменьшении исходного значения шага пропорционально проведенным итерациям. Такая стратегия позволяет бактериям в начале процедуры поиска оптимума исследовать большее пространство за счет длинного шага. Последующее искусственное снижение подвижности заставляет бактерии более подробно исследовать области ранее обнаруженных оптимумов. Результаты эксперимента показали, что при b = 2 алгоритм обеспечивает достаточно стабильный уровень точности решения (изменение погрешности не превышает 0,1), даже при увеличении начального шага в 5 раз.
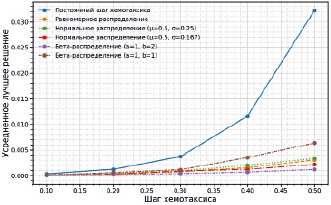
Рис. 5. Влияние закона распределения случайной величины шага на точность решения при параметре β = 2 в (3)
5. Стохастический подход заключается в выборе шага хемотаксиса для каждой бактерии случайным образом в интервале от нуля до значения, соответствующего параметру S0. Для этого в формулу расчета шага вносится некоторая случайная величина, распределенная по какому-либо закону. При оценке эффективности стохастического подхода использовались следующие, известные законы распределения случайных величин: равномерное распределение, нормальное распределение и бета-распределение. Нормальное распределение и бета-распределение тестировались на двух различных наборах параметров. Полученные результаты позволяют утверждать, что использование в ходе хемотаксиса формулы (2) с любым из рассмотренных законов распределения дает всегда лучшие результаты по сравнению с шагом постоянной величины. Из всех рассмотренных законов распределения с заданными параметрами самые точные решения получаются при использовании бета-распределения с параметрами α = 1 и β = 2.
Работа выполнена при поддержке РФФИ, проект № 19-01-00357.



