Важным условием успешного обучения является интерес студентов к изучаемым темам, ходу обучения и его результату. Поэтому надо научить студента учиться, так как общественные изменения и технический прогресс будут заставлять их исследовать конкретные реальные явления [1; 2]. Вопрос об организации самостоятельной работы студентов встает по-новому в связи с внесением этой формы обучающей студента деятельности в государственный образовательный стандарт.
Цель исследования: надо ориентировать студента на приобретение необходимых знаний не только общением с преподавателем, но и самостоятельной познавательной деятельностью и саморазвитием личности.
Новые учебные планы предусматривают выделение значительного числа часов на самостоятельную работу студентов. Отсюда проблема математического обеспечения такой работы.
Материалы и методы исследования
Увеличивающийся объём информации и сокращение времени на её осмысливание требует от преподавателей пересмотра концепций заданий. Задачи с производственным содержанием способствуют качественному изменению знаний, повышению уровня математической культуры студентов [3; 4].
Результаты исследования и их обсуждение
Приведем примеры используемых задач при преподавании дисциплины «Математическое моделирование процессов в компонентах природы» в рамках образовательной программы по направлению подготовки 20.04.02 «Природообустройство и водопользование» в Федеральном государственном бюджетном образовательном учреждении высшего образования «Кубанский государственный аграрный университет имени И.Т. Трубилина».
Задача 1.
Уровень грунтовых вод зависит от антропогенного воздействия, осуществляемого на мелиорируемых территориях. Величина водоподачи и интенсивность дренажного стока влияют на накопление солей в зоне аэрации. Следовательно, уровень грунтовых вод можно рассматривать как функцию этих двух факторов. Оценка оптимальности уровня грунтовых вод и рассоления грунта – основные задачи мелиоративной службы [5; 6].
Задачу рассоления грунта при промывке будем рассматривать в предположении одномерности фильтрационного и солевого потоков. Граница насыщения продвигается в ненасыщенный грунт, который будем считать сухим. В области фильтрации происходит растворение солей твердой фазы и вытеснение засоленного раствора в лежащие ниже слои грунта. На поверхность почвы налит слой воды, который проникает в почву. При этом вблизи поверхности образуется зона насыщения [7; 8].
Рассматриваем три стадии промывки. Первая начинается с момента возникновения зоны насыщения у поверхности почвы и продолжается до тех пор, пока движущаяся граница не достигнет водоупора или поверхности грунтовых вод. Продолжительность первой стадии на практике небольшая. Однако она оказывает существенное влияние на формирование начального профиля засоления почвы [9]. На этой стадии испарением почвы можно пренебречь, так как оно происходит только с водной поверхности и не вызывает восходящих потоков в толще грунта. На второй стадии процессы происходят в полностью насыщенной зоне, размеры которой не изменяются. Длительность второй стадии определяется временем t2 – t1. С момента t2 начинается третья стадия, когда происходит опускание свободной поверхности в глубь почвы, обусловленное испарением со свободной поверхности и оттоком воды в нижележащие слои грунта.
Процессы массопереноса, происходящие на трех стадиях промывки, описываются системой дифференциальных уравнений в частных производных, которые в одномерном случае для однокомпонентного засоления принимают вид
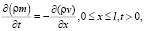 (1)
(1)
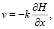
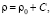 (2)
(2)
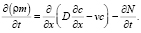 (3)
(3)
Уравнение кинетики растворения соли можно представить в виде
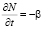 (cН – с)Nn, n = 0; 0,5; 1. (4)
(cН – с)Nn, n = 0; 0,5; 1. (4)
Пористость m фильтрующего вещества предполагается линейно зависящей от давления p: m = m0 + βгр(p – p0), где βгр – коэффициент сжимаемости пласта, m0 – пористость при начальном давлении р0.
Уравнения (1), (2) можно переписать в виде
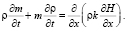 (5)
(5)
Воспользовавшись зависимостями между пористостью и давлением, напором и давлением, перепишем последнее уравнение
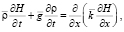 (6)
(6)
где 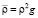 βгр;
βгр; 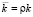 ;
; 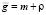 грHg – – ρβгрgx.
грHg – – ρβгрgx.
Решение уравнений (1)–(5) ищем в области
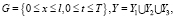
где Yi (i = 1, 2, 3) – области, соответствующие различным стадиям промывки.
Пусть S(t) – координата границы зоны насыщения. Для решения системы необходимо задать начальные и краевые условия, которые зависят от стадии промывки.
На первой стадии на верхней границе задается значение напора как функции времени
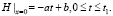 (7)
(7)
Нижняя граница является движущейся свободной поверхностью. Следовательно, на ней напор является функцией координаты границы
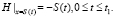 (8)
(8)
Кроме того, на движущейся границе ставится второе условие, связывающее скорость движения границы с градиентом напора. Это условие вытекает из закона сохранения массы
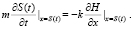 (9)
(9)
Считая концентрацию соли спр в промывной воде величиной постоянной, записываем уравнение конвективной диффузии на поверхности почвы
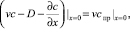
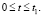 (10)
(10)
Из закона сохранения массы условие на границе S(t) следующее
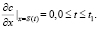 (11)
(11)
При переходе со второй стадии промывки на третью граничные условия на нижней границе области не изменяются. На третьей стадии для уравнения фильтрации на опускающейся верхней свободной поверхности ставятся два условия
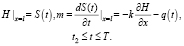 (12)
(12)
Функция q(t) характеризует величину испарения со свободной поверхности. Для уравнения диффузии в точке S(t) (точка верхней свободной поверхности) ставится условие, аналогичное условию для первой стадии промывки.
На первой стадии промывки систему (3)–(5) решаем в области
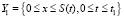
при краевых условиях и начальных условиях
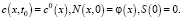 (13)
(13)
На второй стадии промывки система (1.3)–(1.5) решается в области
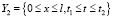
при краевых условиях (7), (10).
При этом за начальные условия принимаются значения, полученные после первого периода промывки.
На третьей стадии промывки G3 == {S(t) ≤ x ≤ l, t2 ≤ t ≤ T} при x = S(t), x = 0 рассматриваются условия (13) и при x = S(t) задаются условия вида (12).
За начальные условия берутся значения напора и концентрации с предыдущего периода промывки.
Задача 2.
Для показателей многих свойств горных пород (коэффициентов пористости, влажности) эмпирические кривые распределения можно описывать кривой нормального распределения. Выполним оценку параметров нормального распределения.
Запишем плотность вероятностей рx(х | q) нормального распределения
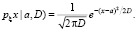 (14)
(14)
Рассмотрим оценку параметров нормального распределения а (математическое ожидание) и D (дисперсия).
Логарифмируя рx(а, D), получим
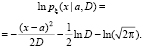 (15)
(15)
Отсюда
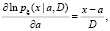
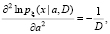 (16)
(16)
и поэтому элемент Iaa информационной матрицы равен
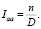 (17)
(17)
Далее
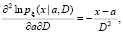
и поэтому
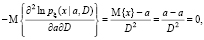
так что IaD = 0.
Наконец,
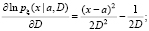
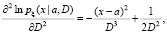
так что
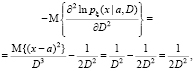
и поэтому
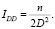
Таким образом, информационная матрица имеет вид 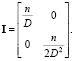
Матрица, обратная информационной, равна 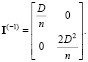
Поэтому минимальные вариации оценок параметров а и D равны
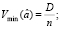
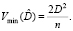
Приступим к построению оценок. Имеется выборка 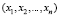 . Так как
. Так как
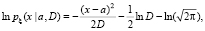
то логарифм функции правдоподобия имеет вид
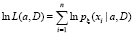 =
=
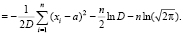
Далее для нахождения оценок 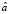 и
и 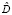 параметров а и D находим частные производные
параметров а и D находим частные производные 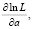
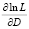 , приравниваем их нулю и составляем систему уравнений
, приравниваем их нулю и составляем систему уравнений
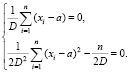
Из которой получаем 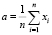 ,
,
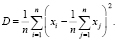
Эти значения аргументов дают оценки неизвестных параметров а и D
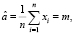 (18)
(18)
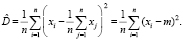 (19)
(19)
Оценку 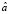 параметра а обычно обозначают как т.
параметра а обычно обозначают как т.
Заключение
Дисциплина «Математическое моделирование процессов в компонентах природы» способствует подготовке будущих специалистов к успешной профессиональной деятельности.
Современное профессиональное образование немыслимо без математического, так как именно оно закладывает фундамент дальнейшего интеллектуального совершенствования, развивает гибкость мыслительной деятельности. При этом требуется организация такого обучения, которое обеспечивало бы переход учебной деятельности в профессиональную, т.е. обучение, способствующее овладению профессионально-прикладной математической компетентностью.
Потому необходимо развивать методическое обеспечение образовательного процесса, готовить к занятиям индивидуальные и дифференцированные задания для студентов. Подготовленные задания приобщат студентов к научно-исследовательской работе, повысят качество их математического образования.



