В работе рассматривается задача выбора рационального распределения работников на задачи наукоемкого проекта для осуществления фундаментальных и прикладных разработок. Для задания времени выполнения работником конкретной задачи предлагается применять нечеткие множества [1, 2]. При этом возникает множество трудностей: задать нечеткие множества, учитывать одновременную работу нескольких сотрудников над одной задачей, определиться с правилами дефаззификации. Рассмотрим проблему определения результирующего нечеткого множества «выполнение задачи» при назначении на нее нескольких работников. Каждый работник, назначенный на данную задачу, имеет нечеткое множество «выполнение задачи одним конкретным работником». Нечеткое множество задано функцией принадлежности времени выполнения задачи, показывающей, сколько времени необходимо работнику для выполнения работы с различной его уверенностью [3, 4]. Так, границы этого множества задаются путем опроса работника и определения оптимистичного, пессимистичного и матожидаемого времени выполнения работы конкретным работником.
В статье [5] предложен алгоритм обобщения нечетких множеств, заданных на различных несущих множествах, при условии монотонности, непрерывности функции принадлежности выполнения задачи работником. Но в ней рассматриваются только функции принадлежности, заданные в виде кусочной линейной функции.
Целью данной работы является рассмотрение возможности применения других функций принадлежности, обладающих свойствами непрерывности и монотонности, для задания нечетких множеств «выполнении задачи работником». Основной идеей предложенного алгоритма обобщения нечетких множеств является поиск значений аргументов всех функций принадлежности нечетких множеств при одном и том же значении функции принадлежности.
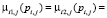
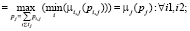 (1)
(1)
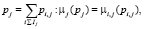
для 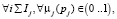 (2)
(2)
где μi1,j, μi2,j и μj – функции принадлежности времени (производительности) выполнения работы j работниками i1, i2 и результирующее соответственно; а pi,j и pj значение времени выполнения работы j (производительности работника).
Материалы и методы исследования
В случае кусочно-линейных функций принадлежности данный поиск сводится к циклическому поиску значений аргументов функций для каждой точки перегиба, так как монотонность и линейность всех функций принадлежности между точками перегиба позволяет судить о линейном характере и обобщенной функции принадлежности. В результате вместо функций можно хранить только множество точек, содержащих значения времени (t) и соответствующего значения функции принадлежности (ν): 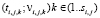 , где si,j – количество точек перегиба функции принадлежности нечеткой функции «выполнение i-м работником j-й задачи». В результате формулы вычисления обобщенной функции принадлежности примут вид
, где si,j – количество точек перегиба функции принадлежности нечеткой функции «выполнение i-м работником j-й задачи». В результате формулы вычисления обобщенной функции принадлежности примут вид
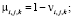 (3)
(3)
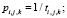 (4)
(4)
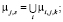 (5)
(5)
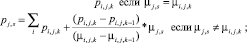 (6)
(6)
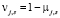 ; (7)
; (7)
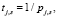 (8)
(8)
где i – номер работника; j – номер задачи; k – номер точки для функции; νi,j,k – k-я точка функции принадлежности нечеткой функции «выполнение задачи работником» для i-го работника, j-й задачи от времени; νi,j,k – k-я точка функции принадлежности нечеткой функции «выполнение задачи работником» для i-го работника, j-й задачи от производительности; ti,j,k – k-е значение времени для i-го работника, j-й задачи; pi,j,k – k-е значение производительности для i-го работника, j-й задачи; μj,s – s-я точка функции принадлежности нечеткой функции «выполнение задачи» для j-й задачи от производительности; μj,s – s-я точка функции принадлежности нечеткой функции «выполнение задачи» для j-й задачи от времени; tj,s – s-е значение времени для j-й задачи; pj,s – s-е значение производительности для j-й задачи.
Для других монотонных, непрерывных функций правила вычисления обобщенной функции принадлежности (1, 2) будут аналогичными. Задача сводится к поиску значений аргумента функции принадлежности для каждого значения функции принадлежности. В данном случае также подойдет алгоритм прохождения по точкам изменения графика функции принадлежности (s), так как между этими интервалами формула обобщенной функции хоть и останется неопределенной, но уравнение функции изменяться не будет. В данном случае основным вопросом является определение уравнения обобщенной функции принадлежности. Функции могут принимать вид, отличный от линейного, и при этом быть непрерывными на ограниченном участке и монотонными, например обратно-пропорциональная, квадратичная, степенная, показательная или логарифмическая. Даже тригонометрические функции на ограниченном участке могут обладать свойством монотонности.
Применение кусочных функций принадлежности, кроме своей вычислительной простоты, обусловлено также и правилами задания функции принадлежности. В статье [5] четко определены правила задания функции принадлежности для случая кусочно-линейной функции путем опроса работника по различным временам выполнения работы. Но данный подход не учитывает историю подобных обращений к работнику, склонен ли он завышать или занижать граничные оценки, предпочитает ли он перестраховаться, искусственно растянув интервал, или же, наоборот, излишне самоуверен. Можно отметить, что в реальных условиях задержка в сроках выполнения задачи может быть неравномерной, например, когда время приближается к планируемому или же больше его, производительность работника резко увеличивается, т.е. характер функции принадлежности ближе к показательной функции.
Для задания такой функции двух граничных точек будет недостаточно. Для этого требуется перечислить возможные с точки зрения программной реализации виды функций. Для определения конкретной функции в программной реализации алгоритма создается динамический массив, в котором хранится тип функции, а также параметры данной функции (ti,j,k; νi,j,k; fi,j,k) (t)).
В результате алгоритм вычисления функции принадлежности с насыщением нечеткой функции «общей» производительности при выполнении выбранной задачи [6] особо не поменяется. Изменения коснутся только шагов по ветке «нет» для условия «Значения функции принадлежности одинаковы?». Вместо вычисления параметров прямой необходимо подставить в соответствующую функцию значения параметров функции и значение функции принадлежности.
При вычислениях (1, 2) необходимо определить для заданного значения функции принадлежности значение производительности. Так как значение функции принадлежности является ординатой, то необходимо использовать заранее вычисленную обратную функцию. Данный подход не всегда возможен, так как у некоторых функций, например параболы, достаточно сложные обратные функции, к тому же имеющие несколько значений абсциссы. В этом случае на сложную аналитическую функцию необходимо наложить ограничения, которые оставят одно решение. Данную задачу придется решать до самих вычислений «общих» функций, при формировании исходных функций принадлежности времени выполнения работником задачи и их параметров. В результате алгоритм останется неизменным.
Результаты исследования и их обсуждение
На сложность вычисления результирующей функции, полученной из обобщения нелинейных «четких» функций принадлежности нечеткой функции «общей» производительности, влияет цель поиска данных функций. В случае решения задачи назначения работников конечной целью алгоритма поиска нечеткой функции «выполнения задачи» является вычисление параметра, по которому будет определяться критерий оценки времени выполнения всех задач. При такой постановке задачи после получения нечеткой функции «выполнения работы» необходимо провести ее дефаззификацию [7].
Самый простой способ дефаззифицировать нечеткую функцию времени выполнения работы – метод правого модального значения. Данный метод применяют для выпуклых «четких» функций принадлежности. В случае если функция принадлежности монотонна и непрерывна, предлагается использовать значение времени, при котором работа точно будет выполнена, т.е. минимальное значение времени, при котором «четкая» функция принадлежности времени выполнения задачи примет значение равное 1. Эта точка в любом случае будет получена в результате вычисления обобщенной функции. В таком случае характер функции принадлежности роли не играет и может вообще не рассматриваться. Подобным образом можно использовать и метод левого модального значения, который будет рассматривать самые оптимистичные сроки выполнения всех задач.
Другим возможным методом дефаззификации является разложение нечеткого множества на обычные множества при помощи α-уровня. Для этого необходимо определить значение уровня из интервала (0; 1). Этот уровень показывает значение времени выполнения задачи, при значении функции принадлежности равной значению α. Физический смысл такого уровня можно объяснить следующим образом: причиной, по которой значение функции принадлежности не равно 0, является надежда работников успеть полностью выполнить задачу при условии, что у них не возникнет непредвиденных трудностей при ее выполнении. В случае же возникновения некоторых трудностей можно с уверенностью предполагать, что к данному моменту времени задача будет выполнена не в полном объеме или не должного качества, но будет близка к завершению. Например, при разработке программного продукта возможно получение ранней, частично рабочей версии. В результате в процессе дефаззификации возможно вычисление нескольких различных значений времени выполнения работы, предположительно находящейся на различных стадиях ее завершения. Для вычисления α-уровня необходимо для каждой обобщенной нечеткой функции добавить точку соответствующую значению α для функции принадлежности. В алгоритме, изображенном на рис. 1, необходимо добавить значение α-уровня в массив точек перед проведением процедуры упорядочивания массива точек.
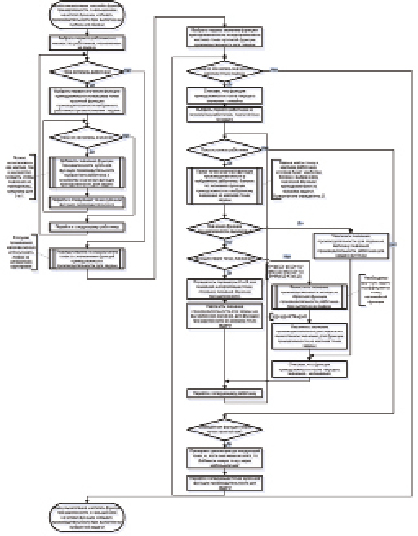
Рис. 1. Алгоритм обобщения функций принадлежности, в том числе и нелинейных, для нечетких функций
Другие способы дефаззификации не могут быть применены на предложенных «четких» функциях принадлежности, для которых выполняются условия непрерывности и монотонности даже при условии задания их в виде кусочно-линейных функций. Для расширения возможностей дефаззификации предлагается вычислить производную функции принадлежности:
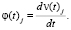 (9)
(9)
Полученная функция может быть рассмотрена как нечеткая функция «время выполнения задачи». Данная функция обладает свойствами непрерывности и в предельных значениях имеет значение функции принадлежности равное 0. Для подобных функций возможно применение других классических методов дефаззификации: метод максимума функции принадлежности, метод центра тяжести, метод медианы, метод центра максимума и т.д. Данные методы требуют знания функции для вычисления различных ее характеристик. В случае кусочно-линейных функций для определения значения производной необходимо вычислить только угол наклона прямой. Для нелинейных функций вычисление производной, в рамках программной реализации, затруднено. При этом следует отметить, что в большинстве случаев в результате процедуры обобщения вычисление самой нелинейной функции в аналитическом виде нереализуемо, тем более вычисление ее производной.
В результате наиболее рациональным подходом к использованию нелинейных функций при «сложных» методах дефаззификации является численное вычисление различных точек функций. Наиболее простым подходом является аппроксимация нелинейной функции методом трапеций в процессе их обобщения. Для этого необходимо в алгоритме (рис. 1) в случае обнаружения нелинейности обобщенной функции добавить точки для функции принадлежности с небольшим шагом для вычисления значений в этих точках. При этом следует помнить, что точки определяются не значением производительности (абсциссы), а значением функции принадлежности (ординаты), которая принимает значения в интервале [0; 1]. Далее в алгоритме для каждого значения функции принадлежности будет вычислено значение «общей» производительности, которое позже будет преобразовано в значение времени. После получения обобщенной нечеткой функции «выполнение задачи» можно переходить к вычислению нечеткой функции «время выполнения задачи» и далее применять алгоритмы дефаззификации. В результате алгоритм примет вид, представленный на рис. 2. При этом непосредственный поиск производной будет производиться в алгоритме дефаззификации.
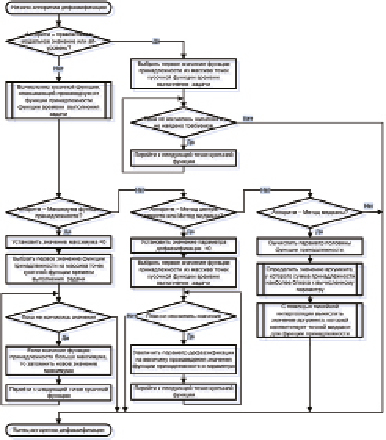
Рис. 2. Алгоритм дефаззификации нечетких функций
Рассмотрим процесс вычисления наиболее распространенных методов дефаззификации при использовании производной функции:
1. Метод центра тяжести. Применение этого метода предусматривает вычисление параметра нечеткой функции по формуле
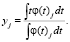 (10)
(10)
Учитывая, что 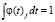 , вычисления центра тяжести сводятся к поиску среднеарифметического значения кусочно-линейной функции
, вычисления центра тяжести сводятся к поиску среднеарифметического значения кусочно-линейной функции 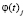 .
.
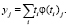 (11)
(11)
2. Метод максимума функции принадлежности.
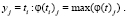 (12)
(12)
3. Метод медианы. Данный метод может дать как некоторое приблизительное значение, так и точное. Для точного значения необходимо на участке нахождения значения провести вычисление уравнения прямой с последующим вычислением значения точки.
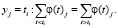 (13)
(13)
В общем виде алгоритм дефаззификации представлен на рис. 2.
Выводы
Необходимость проводить обобщение нечетких функций с нелинейными функциями принадлежности определяется в первую очередь алгоритмом дефаззификации. Для алгоритмов дефаззификации, работающих с одним значением функции принадлежности, например левого и правого модального значения, α-уровня, необходимо вычислить только одно значение, и форма нелинейной функции принадлежности неважна. Такие алгоритмы практически ничем не отличаются от алгоритмов обобщения кусочно-линейных функций принадлежности.
Для более сложных алгоритмов дефаззификации необходимо определить нелинейную функцию принадлежности, что практически невозможно. В данном случае предлагается сначала вычислить обратную нелинейную функцию для использования в качестве аргумента значения функции принадлежности и аппроксимировать эту функцию кусочно-линейной.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта 18-00-00012 (18-00-00011) КОМФИ.



