Машиностроительная промышленность имеет большой потенциал для реализации рекуперативного цикла отработанного тепла. При этом, несмотря на высокий потенциал данного направления, промышленность крайне редко прибегает к реализации данного подхода на производстве [1].
Стоит уделить особое внимание таким отраслям, которые являются наиболее энергоёмкими с высоким уровнем тепловых потерь. Одними из них являются металлургия, химическое производство, производство цемента, металлообрабатывающие производства [1–3]. Лидерами по количеству выброшенного в атмосферу тепла являются сталелитейные предприятия, в которых крупнейшим потребителем энергии является плавильная печь. В данном аппарате тепловые потери составляют значительную часть расхода электроэнергии [3], в особенности в период выдержки металла, и могут достигать ~40 % [4–6], что связано с особенностями принципа действия печи. Возврат этой тепловой энергии в технологическую схему или на нужды предприятия может существенно повысить эффективность всего предприятия [3, 7, 8].
Использование возвращенной тепловой энергии обратно в технологический цикл производства в виде механической энергии, выполненное на основе системы рекуперации тепловых потерь (СРТП), позволяет существенно повысить эффективность как отдельного агрегата, так и всего производства в целом. Одним из ключевых агрегатов в рассмотренной схеме является кожухотрубный теплообменный аппарат, реализующий рекуперацию тепловых потерь от бросового тепла. Так как эффективность всей СРТП зависит от эффективности всего данного теплообменного агрегата, то ключевой целью проведенного исследования является повышение эффективности работы данного теплообменника [9–10]. И так как эффективность теплообменного аппарата (ТА) определяется эффективностью передачи тепла от одного потока к другому и потерями тепла от теплообменного аппарата в окружающую среду [9], которые связаны с тем, что поверхность ТА имеет температуру, более высокую, чем окружающая среда. При этом интенсивность внешних тепловых потерь носит сегментный характер, так как в разных частях внешней поверхности температура может быть различна. Значит, секционное распределение тепловой изоляции может улучшить массогабаритные характеристики ТА без потери его эффективности.
Поэтому в данной работе проведен сравнительный анализ эффективности изолирования различных участков внешней поверхности кожуха теплообменника при разных давлениях вакуума. Выбор данной конструкции ТА обоснован тем, что она является наиболее простой и может эксплуатироваться при высоких рабочих давлениях и температурах [11–12].
Объектом исследования является рекуперативный противоточный кожухотрубный ТА, имеющий длину 2,1 м (рис. 1).
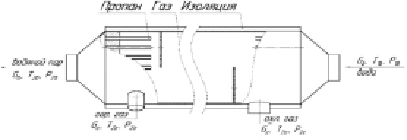
Рис. 1. Конструкция теплообменного аппарата
В теплообменном аппарате используются два теплоносителя: нагревающий – газ, нагреваемый – вода. Схема движения теплоносителей – противоток. Внутри кожуха ТА располагается трубный пучок, состоящий из 37 трубок диаметром 6 мм с толщиной стенки 1 мм, расположенный в форме равностороннего шестиугольника. Длина трубок составляет 2,0 м. Внешний диаметр кожуха ТА составляет 0,063 м, с толщиной стенки 1,5 мм. По всей длине ТА равномерно расположены перегородки с шагом 0,2 м, имеющие толщину 2 мм, которые выполняют функцию перераспределения потока газа внутри ТА с целью устранения застойных зон и налаживания эффективного теплообмена между теплоносителями.
Изоляция внешней поверхности кожуха представляет собой герметичную цилиндрическую оболочку с откачанным из неё воздухом, выполненную из нескольких блоков. Толщина вакуумной изоляции 20 мм. Анализ теплообменных процессов внутри ТА выполняется для следующих степеней покрытия кожуха блоками вакуумной изоляции: 0; 25; 50 и 100 %. Покрытие кожуха блочной вакуумной изоляцией начинается с участка подачи горячих газов и движется в сторону их выхода из ТА.
Моделирование теплообменных процессов, протекающих в рекуперативном ТА, выполнялось с использованием программного обеспечения ANSYS Fluent. Моделируя протекающие в ТА процессы, приняли ряд граничных условий: температура охлаждаемого газа на входе в ТА (Тг) равная 600 °С; температура нагреваемой воды на входе в ТА (ТВ) равна 18 °С и температура окружающей среды (Тн) равна 20 °С, с постоянным коэффициентом теплоотдачи между окружающей средой и внешней поверхностью кожуха ТА (α) равным 5 Вт/(м2·К).
Материалы и методы исследования
Моделирование процессов, протекающих внутри ТА, выполняется в программном обеспечении ANSYS Fluent в следующей последовательности [9–11]:
1. Выполняется трехмерная модель ТА в CAD-системе и сохраняется с расширением «.x_t» (рис. 2).
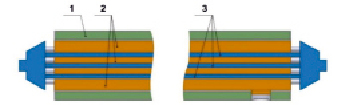
Рис. 2. Расчётная трехмерная модель, выполненная в Solidworks: 1 – изоляция; 2 – горячий воздух; 3 – вода
Рис. 3. Трехмерная модель ТА в блоке Geometry с долей изоляции: 0; 25; 50; 75 и 100 %
2. Полученная трехмерная модель импортируется в программу ANSYS Workbench Fluent, раздел настройки геометрии Geometry (рис. 3). Так как в данном проекте имеется связь solid – fluid (твердое тело – жидкая среда), то всю модель можно объединить в один parts (блок). При моделировании теплообменных процессов с разной зональностью вакуумной изоляции, лишние участки изоляции можно отключить в дереве модели, тем самым исключив их из проводимого анализа.
3. Выполняется настройка и генерация сеточной модели ТА. Для описания явлений, происходящих в ТА, необходимо обеспечить определенное значение безразмерного коэффициента высоты первой пристеночной ячейки.
4. Настраиваются все необходимые для выполнения расчета граничные условия:
4.1. В разделе Model задаются параметры используемых в расчете моделей:
а) устанавливается RNG k-epsilon модель турбулентности, использующая уравнения переноса турбулентной кинетической энергии k и её скорости диссипации ε (1–2). Также необходимо указать поверхности участвующие в процессе теплового излучения и выполнить расчет угловых коэффициентов.
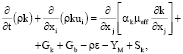(1)
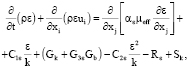(2)
где Gk – это производство турбулентной кинетической энергии, вызванное градиентами осредненного потока; Gb – производство турбулентной кинетической энергии, вызванное плавучестью; YM – параметр, характеризующий пульсации, вызванные расширением в сжимаемых турбулентных потоках; С1ε и С2ε – эмпирические константы модели; αk и αε – эффективные числа Прандтля для k и ε; Rε – модификатор ренормализации (коэффициент, подавляющий возникновение чрезмерных диффузий); μeff – коэффициент эффективной вязкости; Sk и Sε – источники, определяемые пользователем;
б) следующей подключается модель теплообмена, использующая уравнение переноса энергии в текучей среде – дифференциальное уравнение конвективного теплообмена Фурье – Кирхгофа:
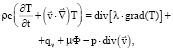(3)
где ρ – плотность; c – удельная массовая теплоемкость; t – время;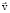 
– вектор скорости движения вещества; λ – коэффициент теплопроводности вещества; qv – источниковый член уравнения, выражающий изменение энергии под действием внутренних источников теплоты; μ – динамический коэффициент вязкости; Ф – диссипативная функция;
в) подключается модель радиационного теплообмена Surface to Surface (S2S) (от поверхности к поверхности), физическая основа которого в том, что используются уравнения межповерхностного лучистого теплообмена методом угловых коэффициентов между поверхностями i и j [13]. Для этого используется фактор видимости Fij поверхности Ai и Aj, который показывает, насколько хорошо видна поверхность Aj с поверхности Ai. Для бесконечно малых поверхностей dAj и dAi можно будет найти коэффициент видимости Fij согласно уравнению (4), при условии, что обе поверхности имеют конечные площади.
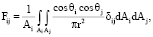(4)
где A – площадь поверхности; δijj – коэффициент видимости от dAj до dAi, если dAj виден dAi, то значение 1, иначе 0; θi и θj – углы между единичными нормалями к поверхностям; rij – расстояние между поверхностями.
Для нахождения энергии, отраженной от поверхности i, используется уравнение
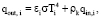(5)
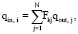
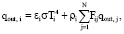
где εi – коэффициент излучения поверхности; Тi – температура поверхности i; σ – постоянная Стефана – Больцмана; qin,i – поток падающей энергии;
г) задается модель фазового состояния Volume of Fluent (VOF) (модель свободного объема) с зональными дискретизациями Zonal Discretization, двумя эйлеровыми фазами и с учетом неявной силы тяжести Implicit Body Force.
4.2. Зонам присваиваются созданные материалы с установленными температурно-зависимыми свойствами (помимо этого выставляем значения молярной массы).
4.3. Настраиваем фазовое взаимодействие Phase Interaction: массовый перенос Mass Transfer и поверхностное натяжение Surface Tension в зависимости от температуры, по жидкой фазе.
4.4. Задаются граничные условия потоков воды и газа (массовый расход на входе и давление на выходе, а также характеристики материалов).
4.5. Устанавливаются настройки мониторинга расчета.
4.6. Выставляются начальные параметры расчета, с учетом контроля числа Куранта, которые будут корректироваться со временем (рекомендуется не превышать значение числа Куранта 50).
5. Производится запуск и контроль выполняемого расчета.
6. Выполняется визуализация и обработка полученных результатов в программе CFD-Post.
Моделирование данного теплового анализа выполняется с использованием половины ТА с продольным сечением. Данное решение принято для того, чтобы уменьшить нагрузку на используемую для проведения расчета машину. Для реализации данной модели используется операция symmetry, позволяющая выполнять расчет с учетом зеркальности относительно указанной плоскости.
На рис. 4 представлено распределение температуры на внешней поверхности кожуха рекуперативного ТА при различной степени изолированности кожуха [14–15].
а)
б)
в)
г)
д)
Рис. 4. Распределение температуры на внешней поверхности кожуха рекуперативного ТА: а) 0 % изоляции; б) 25 % изоляции; в) 50 % изоляции; г) 75 % изоляции; д) 100 % изоляции
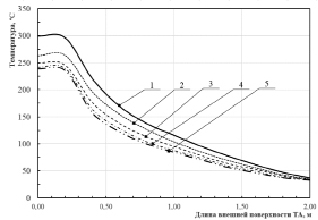
Рис. 5. График зависимости распределения температуры на внешней поверхности рекуперативного ТА по его длине: 1 – 0 %; 2 – 25 %; 3 – 50 %; 4 – 75 %; 5 – 100 %
На рис. 5 представлен график среднего значения температуры на внешней поверхности ТА.
Из рис. 5 видно, что первая четверть внешней поверхности ТА характеризуется наиболее высокими температурами. При этом изолирование второй половины внешней поверхности ТА существенного влияния на значение тепловых потерь не оказывает.
На рис. 6 представлен график зависимости тепловых потерь в процентных соотношениях от степени изоляции кожуха ТА при различных давлениях газа в вакуумной изоляции.
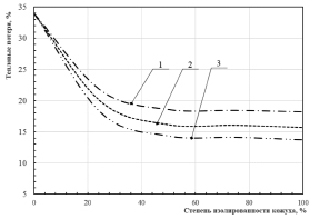
Рис. 6. График зависимости тепловых потерь от степени изолированности кожуха ТА при разных давлениях вакуумной изоляции: 1 – 0,01 атм; 2 – 0,4 атм; 3 – 1 атм
Результаты исследования и их обсуждение
Анализируя полученные данные представленных на рис. 6 графиков, можно сказать, что существенное снижение тепловых потерь возникает при изоляции участка в 25 % поверхности кожуха. После изолирования участка в 50 % поверхности кожуха ТА изменения в количестве тепловых потерь не столь существенны. Также получены данные о том, что повышение давления вакуума ведет к снижению эффективности изоляции на ~5 %. Это связано с тем, что при низком давлении вакуума в процессе теплообмена участвует только передача тепла с помощью излучения.
Заключение
В данной работе проведен сравнительный анализ эффективности изолирования вакуумной изоляцией различных участков внешней поверхности кожуха теплообменника при разных давлениях вакуума. Расчёт выполнен в среде Ansys (FluidFlow Fluent). Анализ результатов показал, что с ростом давления в изоляции в процессе теплопередачи начинает участвовать конвективный теплообмен, что приводит к ухудшению эффективности работы ТА с ~13,5 % до ~18,5 %. Также показано, что максимальный прирост эффективности тепловой изоляции имеет место на участке подачи горячего газа (25 % изолированной поверхности).