Для прогнозирования состояния информационного канала необходимо знать степень воздействия различных возмущающих факторов на характеристики передаваемых сигналов. Особенно это важно при отсутствии возможности экспериментальной проверки возникающих искажений сигнала. В таких условиях решающую роль играет математическое моделирование процесса передачи сигнала в возмущенном канале. Для решения ряда практических задач определяющее значение имеет оперативность оценки возможных искажений сигналов при распространении в канале. Последнее обстоятельство вынуждает искать пути упрощения и оптимизации алгоритмов расчетов характеристик сигнала.
Одним из эффективных методов оценки состояния информационного канала является метод многочастотного доплеровского просвечивания [1]. Преимуществами этого метода являются: повышенная чувствительность к малым изменениям среды канала, высокое временное разрешение, сравнительная простота и дешевизна аппаратурных решений, а также возможность организации непрерывных наблюдений. Для решения практической задачи многочастотного просвечивания стохастического канала полезным является математическое моделирование ожидаемых доплеровских характеристик сигнала в условиях пространственно-временных случайных возмущений.
Для расчета характеристик сигнала в информационном канале широко используется лучевое приближение [2]. Под влиянием возмущений канала лучи могут изменять направление распространения и формировать сложную структуру сигнала. Хорошо известным методом расчета влияния случайных неоднородностей канала на траекторные характеристики сигнала является метод статистических испытаний, основанный на численной схеме Монте-Карло [3]. Однако при фиксированной дистанции между корреспондентами эта схема не всегда оптимальна для расчета. Возникающая здесь проблема в первую очередь связана с трудностями численного решения краевой задачи для стохастических дифференциальных уравнений, описывающих процесс распространения сигнала. Для каждой реализации пространственно-временного распределения неоднородностей канала необходимо выполнение граничного условия для траекторий сигнала в пункте приема. Последнее не только требует больших вычислительных ресурсов для проведения расчетов, но и может сопровождаться потерей устойчивости самой схемы расчета. Другим вариантом расчета флуктуаций характеристик сигнала является приближенное аналитическое решение стохастических дифференциальных уравнений с последующим усреднением квадратур и введением физических представлений о корреляционных свойствах неоднородностей канала. Численная реализация усредненных квадратур является завершающей стадией метода численно-аналитического расчета статистических моментов сигнала [4].
Цель настоящей работы заключается в развитии метода численно-аналитического моделирования частотных флуктуаций сигнала в задаче многочастотного доплеровского просвечивания информационного канала, подверженного пространственно-временным случайным воздействиям.
Основные теоретические соотношения
В приближении геометрической оптики [5] расчет доплеровского смещения частоты сигнала при многочастотном просвечивании стохастического информационного канала сводится к интегрированию дифференциального уравнения:
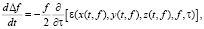 (1)
(1)
где ε(x, y, z, f, τ) – случайная функция, характеризующая диэлектрическую проницаемость канала, τ – время, x(t), y(t), z(t) – случайные функции, описывающие траекторию луча, f – рабочая частота просвечивания, Δf – доплеровский сдвиг частоты, dt – элемент времени группового запаздывания. Случайную траекторию луча в формуле (1) можно определить, решая уравнение эйконала методом характеристик [5]. Для расчетов будем использовать лучевые уравнения в виде
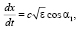
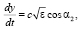
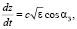 (2)
(2)
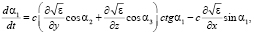 (3)
(3)
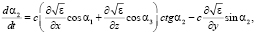 (4)
(4)
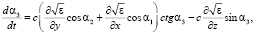 (5)
(5)
где cos α1, cos α2, cos α3 – направляющие косинусы луча в декартовой системе координат.
Уравнения (1)–(5) были решены методом прямого разложения Пуанкаре [6]. Диэлектрическая проницаемость канала представлялась в виде суммы средней составляющей 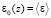 и случайного воздействия
и случайного воздействия 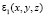 , (
, (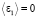 ) при условии
) при условии 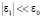 . Решение уравнений (1)–(5) определялось в виде разложений:
. Решение уравнений (1)–(5) определялось в виде разложений: 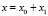 ,
, 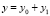 ,
, 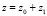 ,
, 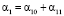 ,
, 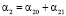 ,
, 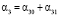 ,
, 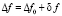 . Здесь
. Здесь 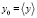 ,
, 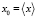 ,
, 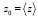 ,
, 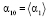 ,
, 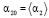 ,
, 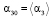 ,
, 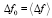 – средние характеристики сигнала;
– средние характеристики сигнала; 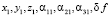 – малые флуктуации характеристик. Подставляя эти разложения в (1)–(5) и полагая, что средняя траектория лежит в плоскости Z0X (
– малые флуктуации характеристик. Подставляя эти разложения в (1)–(5) и полагая, что средняя траектория лежит в плоскости Z0X (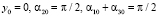 ), для расчета флуктуаций доплеровского смещения частоты сигнала, прошедшего заданную дистанцию, в первом приближении имеем уравнение
), для расчета флуктуаций доплеровского смещения частоты сигнала, прошедшего заданную дистанцию, в первом приближении имеем уравнение
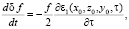 (6)
(6)
где средняя траектория есть решение системы уравнений
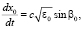
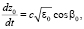
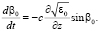 (7)
(7)
Здесь β0 – текущий угол рефракции луча относительно вертикальной оси Z. При выводе (6) предполагалось, что скорость движения хаотических неоднородностей существенно больше скорости движения средней диэлектрической проницаемости канала 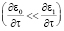 . Уравнения (6), (7) были решены с краевыми условиями
. Уравнения (6), (7) были решены с краевыми условиями
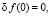
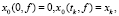
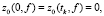 (8)
(8)
где tk – групповая задержка сигнала в пункте приема xk. Интегрируя (6) и проводя усреднение по всем реализациям флуктуаций диэлектрической проницаемости, для дисперсии доплеровского сдвига частоты сигнала имеем
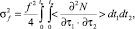 (9)
(9)
где 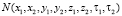 – пространственно-временная корреляционная функция случайного поля неоднородностей канала. Полагая, что поле неоднородностей обладает свойствами квазистационарности и квазиоднородности [5], функцию корреляции можно представить в виде
– пространственно-временная корреляционная функция случайного поля неоднородностей канала. Полагая, что поле неоднородностей обладает свойствами квазистационарности и квазиоднородности [5], функцию корреляции можно представить в виде
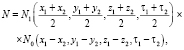 (10)
(10)
где τ1, τ2 – последовательные моменты времени, а функция N1 меняется более медленно, по сравнению с функцией N0.
Для расчета интеграла (9) необходимо задать явный вид функции N. В общем случае эта функция неизвестна. Между тем оценка флуктуаций доплеровского смещения частоты сигнала в информационном канале возможна на основе модели случайно-неоднородной среды канала с обобщенными (интегральными) свойствами. В данном направлении были получены важные результаты благодаря введению представлений о гауссовом корреляционном эллипсоиде, эффективно описывающих случайные неоднородности среды [7] и позволяющих существенно упростить аналитические расчеты статистических моментов сигнала. Следует заметить, что реальные информационные каналы могут содержать хаотические неоднородности многих масштабов, которые описываются степенным спектром [5]. Тем не менее при расчетах низших моментов фазовых флуктуаций сигнала можно использовать гауссов спектр неоднородностей с эффективными параметрами. В частности, исследования показали, что при расчетах дисперсии фазы сигнала в многомасштабной случайно-неоднородной среде канала можно использовать гауссову модель корреляционного эллипсоида, если в качестве пространственного масштаба неоднородностей считать внешний масштаб турбулентности, заданной степенным спектром. Связано это с тем, что высокочастотная часть спектра неоднородностей в большей степени оказывает влияние на амплитуду сигнала и в меньшей степени на его фазу [5].
Для однородной части корреляционной функции канала используем гауссову форму, а движение случайных неоднородностей учтем в рамках гипотезы о замороженном переносе [5]. Тогда однородная часть корреляционной функции (10) будет иметь вид
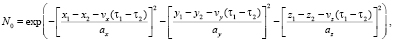 (11)
(11)
где vx, vy, vz – продольная, поперечная и вертикальная скорости движения поля неоднородностей соответственно; ax, ay, az – внешние масштабы турбулентности канала.
Вычисляя интеграл (9) методом суммарно-разностного интегрирования по разностной переменной и полагая для простоты 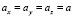 , для дисперсии доплеровского смещения частоты при движении поля неоднородностей вдоль осей X, Y, Z соответственно имеем
, для дисперсии доплеровского смещения частоты при движении поля неоднородностей вдоль осей X, Y, Z соответственно имеем
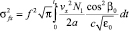 ,
, 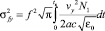 ,
, 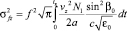 . (12)
. (12)
Следуя методу алгоритмизации, предложенному в [4], интегральные формулы (12) можно преобразовать к обыкновенным дифференциальным уравнениям первого порядка:
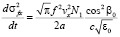 ,
, 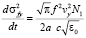 ,
, 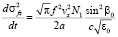 . (13)
. (13)
Совместное численное решение уравнений (13) и (7) позволяет определить дисперсии доплеровского смещения частоты сигналов на различных рабочих частотах при заданной дистанции между пунктами излучения и приема. Заметим, что решения усредненных лучевых уравнений, входящих в систему (7), находятся путем пристрелки траекторий в пункт наблюдения для каждой рабочей частоты просвечивания. В то же время уравнения системы (13) интегрируются с начальными условиями. Таким образом, решение исходной краевой стохастической задачи для обращения данных многочастотного доплеровского просвечивания канала существенно упрощается.
В частном случае линейного слоя, когда 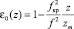 , уравнения (13) с начальными условиями
, уравнения (13) с начальными условиями 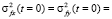
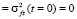 имеют аналитические решения:
имеют аналитические решения:
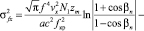
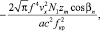
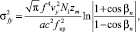
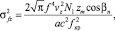 (14)
(14)
где βn – начальный угол входа луча в канал.
Для решения системы (13), (7) был разработан численный алгоритм. Тестирование алгоритма показало его хорошую точность. На рис. 1 приведены среднеквадратичные значения σfx, σfy, σfz, рассчитанные с помощью системы (13), (7) и по формулам (14).
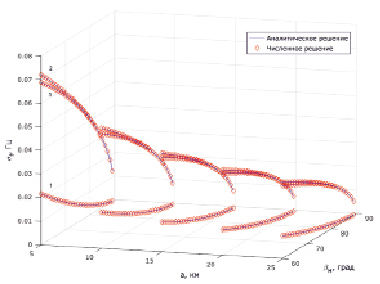
Рис. 1. Зависимости σf от угла βn и масштаба неоднородности a. Параметры возмущенного линейного слоя: zm = 300 км, fкр = 5 МГц, v = 0,1 км/c (где v принимает значения vx, vy или vz), N1 = 10–6, f = 10 МГц. Кривые 1, 2, 3 соответствуют движению поля неоднородностей вдоль осей X, Y, Z и характеризуют σfx , σfy , σf
Пример реализации метода расчета частотных флуктуаций сигнала при многочастотном просвечивании стохастического канала
В качестве примера для демонстрации работы аппарата численно-аналитического моделирования, на рис. 2 приведены результаты расчетов на основе системы (13), (7) частотной зависимости среднеквадратичных отклонений доплеровского смещения частоты сигнала при просвечивании двухслойного канала с крупномасштабным возмущением интенсивных хаотических неоднородностей диэлектрической проницаемости.
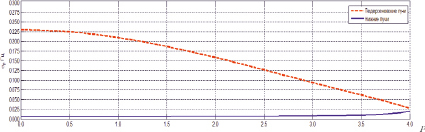
Рис. 2. Среднеквадратичные значения доплеровского сдвига частоты сигнала на различных частотах просвечивания канала. f(p) = f0 + bp2, b = 0,025, f0 = 13 Мгц, zm = 300 км, zmE = 125 км, hm = 100 км, hmE = 25 км, fкр = 6 Мгц, fкр E = 3 Мгц, L = 500 км, χ = 0,1, xL = 500 км, a = 10 км, vz = 100 м/с, xk = 1500 км
Модель средней диэлектрической проницаемости канала представлялась зависимостью
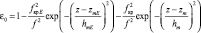 ,
,
где zm, zmE, hm, hmE, fкр, fкр E – высоты минимумов, полутолщины и критические частоты слоев канала. Модель неоднородной части корреляционной функции, характеризующей крупномасштабное локализованное образование хаотических неоднородностей, была задана в виде
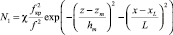 ,
,
где L, χ, xL – размер, интенсивность и координата центра возмущения соответственно. Из рис. 2, в частности, следует значительный рост флуктуаций доплеровского сдвига частоты верхних (педерсеновских) лучей [2] на более низких рабочих частотах.



