Доставка заказов клиентам в определенные сроки предполагает решение двух задач: поиск оптимального маршрута доставки и оптимальное размещение заказов (3DBPСG) в имеющемся транспорте. Первая задача позволяет сэкономить транспортные расходы компании, занимающейся перевозками, вторая – экономить ресурсы, в частности число единиц используемого транспорта для осуществления перевозок. Поскольку задачи маршрутизации и задачи трехмерной упаковки являются трудными задачами дискретной оптимизации, для их практической реализации используются различные эвристики. Предлагается к рассмотрению задача VP_М, возникшая в компании, занимающейся доставкой заказов химической продукции в различные регионы России. Компания арендует автомобильные транспортные средства различной вместимости, имеет ряд депо. Перед отправкой заказ размещается в емкости, имеющей форму параллелепипеда, все автомобильные транспортные средства, загруженные заказом различных клиентов, выезжают из депо, а после обслуживания клиентов возвращаются обратно в депо, при этом по пути следования допускается остановка в определенные часы. Требуется определить наилучшие маршруты доставки заказов различным клиентам с наименьшими расходами (аренда автомобиля, платные дороги), а также организовать рациональную упаковку заказов в автомобильные транспортные средства.
Математическая модель задачи VP_М
В основу математической модели рассматриваемой задачи VP_М легли ограничения из следующих известных задач: задача маршрутизации с учетом вместимости автомобильных транспортных средств (CVRP) [1]; задача маршрутизации с учетом упаковки заказов (3L-CVRP) [2]; задача маршрутизации с временным интервалом (VRPTW) [3], задача маршрутизации с различными депо (MDVRP) [4], задача маршрутизации с возможностью доставки заказа в одном транспортном средстве различным клиентам (SDVRP) [5], задача маршрутизации с возможностью возврата заказа по требованию клиента (VRPPD) [6]; задача маршрутизации EVRP [7]. Обозначения для описания задачи VP_М, являющейся модификацией задачи EVRP, введенные в перечисленных задачах, сохраняются.
Примем в качестве модели дорог, по которым заказ будет доставлен различным клиентам, ориентированный граф, в котором вершины делятся на следующие непересекающиеся подмножества: подмножество вершин (города доставки заказа) Vc = {1,…,n} и подмножество вершин (депо) Vh = {0, n + 1,…,n + k}. Обозначим через mu – количество автомобильных транспортных средств, находящихся в депо (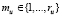 ); ru – число автомобильных транспортных средств, расположенных в депо; известны характеристики кузова автомобильных транспортных средств и их вместимости: Wv – ширина кузова автомобильного транспортного средства v, Lv – длина кузова автомобильного транспортного средства v, Hv – высота, Qv – вместимость. Заказ размещается в емкости, имеющие форму параллелепипеда, известны их характеристики: lpkp – длина емкости kp, wpkp – ширина, hpkp – высота, mpkp – масса емкости kp (Itempar – количество емкостей). Известны потребности клиентов
); ru – число автомобильных транспортных средств, расположенных в депо; известны характеристики кузова автомобильных транспортных средств и их вместимости: Wv – ширина кузова автомобильного транспортного средства v, Lv – длина кузова автомобильного транспортного средства v, Hv – высота, Qv – вместимость. Заказ размещается в емкости, имеющие форму параллелепипеда, известны их характеристики: lpkp – длина емкости kp, wpkp – ширина, hpkp – высота, mpkp – масса емкости kp (Itempar – количество емкостей). Известны потребности клиентов 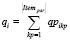 , имеется информация о заказе, который требуют возвратить клиенты:
, имеется информация о заказе, который требуют возвратить клиенты: 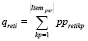 . Компания имеет затраты costpetrolv на бензин, costrentv – затраты на арендную плату автомобильных транспортных средств. По пути следования могут встретиться платные дороги, тогда в транспортные расходы включается и величина costroadij. Кроме того, возможна остановка транспортного средства в определенные промежутки времени [ai, bi]. Пусть cij – время между посещением клиентов, si – время, в течение которого выполняется заказ для некоторого клиента. При этом вводится денежный штраф penalty_timei за обслуживание после заданного времени bi; wiv – время, в которое начинает обслуживаться клиент с прибывшим для него заказом; tiv – время, в которое автомобильное транспортное средство прибывает из депо к клиенту. Решение задачи – переменная xijv , равная 1 при условии, что транспортное средство прибывает из депо от клиента i к клиенту j, и 0 в противном случае. Количество заказа, доставляемого транспортным средством для каждого клиента, – это величина
. Компания имеет затраты costpetrolv на бензин, costrentv – затраты на арендную плату автомобильных транспортных средств. По пути следования могут встретиться платные дороги, тогда в транспортные расходы включается и величина costroadij. Кроме того, возможна остановка транспортного средства в определенные промежутки времени [ai, bi]. Пусть cij – время между посещением клиентов, si – время, в течение которого выполняется заказ для некоторого клиента. При этом вводится денежный штраф penalty_timei за обслуживание после заданного времени bi; wiv – время, в которое начинает обслуживаться клиент с прибывшим для него заказом; tiv – время, в которое автомобильное транспортное средство прибывает из депо к клиенту. Решение задачи – переменная xijv , равная 1 при условии, что транспортное средство прибывает из депо от клиента i к клиенту j, и 0 в противном случае. Количество заказа, доставляемого транспортным средством для каждого клиента, – это величина 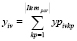 . Если есть заказ, который следует принять обратно от клиента, то его количество вычисляется как
. Если есть заказ, который следует принять обратно от клиента, то его количество вычисляется как 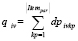 . Вводится денежный штраф penalty_packν за маршрут, в котором не удалось рационально разместить заказы клиентов в транспортное средство. Для того чтобы знать, помещается ли
. Вводится денежный штраф penalty_packν за маршрут, в котором не удалось рационально разместить заказы клиентов в транспортное средство. Для того чтобы знать, помещается ли 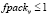 заказ в транспортное средство, вводится параметр fpackν: при выполнении условия заказ помещается в транспортное средство; если fpackν > 1, то заказ не помещается.
заказ в транспортное средство, вводится параметр fpackν: при выполнении условия заказ помещается в транспортное средство; если fpackν > 1, то заказ не помещается.
Математическая модель задачи VP_М:
Найти наименьшие транспортные расходы:
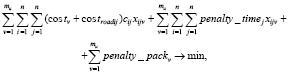 (1)
(1)
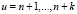
при выполнении следующих условий:
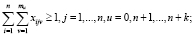 (2)
(2)
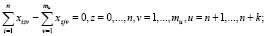 (3)
(3)
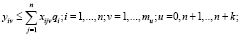 (4)
(4)
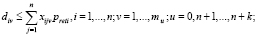 (5)
(5)
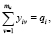
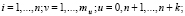 (6)
(6)
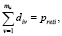
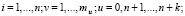 (7)
(7)
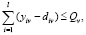
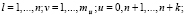 (8)
(8)
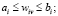
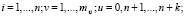 (9)
(9)
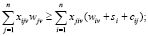
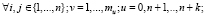 (10)
(10)
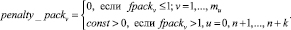 (11)
(11)
Для реализации условия (11) решается задача трехмерной упаковки 3DBPСG, цель которой – минимизация количества транспортных средств с укомплектованными в них палетами с емкостями:
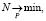 (12)
(12)
где P – множество всевозможных расположений емкостей. При этом выполняются следующие ограничения: емкости не находятся за границей палеты; стороны емкостей параллельны граням палеты; стороны палеты параллельны граням области загрузки транспортного средства; палеты в одном транспортном средстве взаимно не перекрываются; палеты не выходят за пределы транспортного средства; максимальная высота Hmax укомплектованных на палете емкостей не превосходит максимально допустимую высоту hpod max палеты:
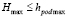 ; (13)
; (13)
стороны емкостей параллельны граням области загрузки транспортного средства; масса укомплектованных на палете емкостей не превышает допустимой вместимости qpod палеты: 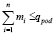 , где mi – масса i-ой емкости. Практически эффективность трехмерной упаковки принято оценивать следующим параметром – коэффициентом упаковки:
, где mi – масса i-ой емкости. Практически эффективность трехмерной упаковки принято оценивать следующим параметром – коэффициентом упаковки:
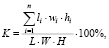
где 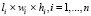 – размеры емкостей, имеющих форму параллелепипеда, W – ширина кузова размещения транспортного средства (параллелепипед), соответственно, L – длина и Н – высота.
– размеры емкостей, имеющих форму параллелепипеда, W – ширина кузова размещения транспортного средства (параллелепипед), соответственно, L – длина и Н – высота.
Упаковка палет с емкостями в транспортное средство осуществляется с учетом центра масс, причем при погрузке следует учитывать, что центр масс укомплектованного автомобильного транспортного средства должен быть в цилиндрической области допущения G:
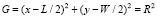 ,
, 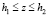 , (14)
, (14)
где x, y, z – координаты емкости в транспортном средстве, R – радиус основания цилиндра, h1, h2 – границы допустимой высоты области G [8].
Следует так разместить палеты с емкостями, чтобы минимизировать девиацию центра тяжести упакованного транспортного средства:
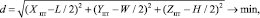 (15)
(15)
где в формуле (15) используются обозначения (Xцт, Yцт, Zцт) для координат центра масс заказов, упакованных в транспорт для отправки;
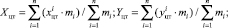 (16)
(16)
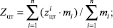 (17)
(17)
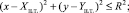 (18)
(18)
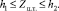 (19)
(19)
Метод решения задачи VP_ М
Для решения задачи VP_М разработан алгоритм ACР-VP_М, являющийся модификацией алгоритма P-ACO-EVRP [9] и алгоритмов [10, 11], для решения задачи 3DBPСG – алгоритм (1,4)-ЕА, являющийся модификацией известного эволюционного алгоритма (μ, λ)-EA [11].
Общая схема алгоритма ACР-VP_М
Шаг 1. Преобразовать исходный ориентированный граф (модель дорог) в матрицу расстояний между клиентами.
Шаг 2. Преобразовать матрицу расстояний в матрицу стоимостей.
Шаг 3. Распределить заказы клиентов по депо и транспортным средствам.
Шаг 4. Поиск квазиоптимальных маршрутов (по критерию минимальной стоимости):
Шаг 4.1. Формировать маршруты с учетом ограничений (1)–(11).
Шаг 4.2. Сформировать популяцию квазиоптимальных маршрутов из маршрутов, полученных на шаге 4.1.
Шаг 4.3. Получить таблицу размещения заказов по транспортным средствам (алгоритм (1,4)-ЕА с учетом (12)–(19)).
Шаг 4.4. Преобразовать популяцию квазиоптимальных маршрутов.
Было разработано программное обеспечение на языке C++, реализующее алгоритм ACР-VP_М. Приведем численный эксперимент, проводимый на тестах, в которые включена следующая информация: местоположения депо и клиентов (координаты), спрос каждого клиента, вместимости арендуемого компанией автомобильного грузового транспорта. Разработанный алгоритм сравнивался с результатами алгоритма P-ACO-EVRP. Результаты экспериментов приведены в табл. 1. Для корректного сравнения результатов алгоритмов в качестве целевой функции взята длина искомого маршрута.
Таблица 1
Сравнение результатов работы алгоритмов ACР-VP_М и P-ACO-EVRP
|
Количество клиентов |
P-ACO-EVRP |
ACР-VP_М |
|
Лучшее решение (длина маршрута доставки) |
Лучшее решение (длина маршрута доставки) |
|
|
200 |
6471,98 |
6354,51 |
|
255 |
588,34 |
596,89 |
|
300 |
1005,12 |
1018,74 |
|
399 |
929,5 |
852,84 |
|
420 |
1833,55 |
1799,57 |
|
480 |
13807,2 |
13602,3 |
Как видно из результатов эксперимента, целевая функция – длина маршрута – при количестве клиентов 200, 399, 420, 480 оказалась лучше в модифицированном алгоритме ACР-VP_М по сравнению с алгоритмом P-ACO-EVRP.
Следующий эксперимент (табл. 2) проводился для того, чтобы оценить вычислительные возможности разработанного алгоритма ACР-VP_М в зависимости от количества клиентов, подавших заявки на доставку заказа. При проведении численного эксперимента использовались тесты с различным количеством клиентов из международной библиотеки тестов OR-Library для тестирования задач исследования (http://people.brunel.ac.uk/~mastjjb/jeb/info.html).
Таблица 2
Среднее время выполнения алгоритма ACР-VP_М
|
количество клиентов |
среднее время работы алгоритма 2000 итераций (сек) |
|
10 |
0,1 |
|
20 |
0,2 |
|
30 |
1,12 |
|
40 |
1,47 |
|
50 |
1,89 |
|
60 |
5,01 |
|
70 |
8,1 |
|
80 |
9,6 |
|
90 |
23,5 |
|
100 |
33,9 |
|
150 |
176,8 |
|
200 |
338 |
|
250 |
6876 |
|
300 |
7798 |
|
420 |
13876 |
|
480 |
1498 |
Заключение
Обсуждались задача поиска квазиоптимальных маршрутов для доставки заказов различным клиентам по критерию минимума транспортных расходов, а также задача трехмерной упаковки, целью которой являлась экономия количества арендуемых компанией транспортных средств с учетом различных ограничений, встречающихся в реальных перевозках. Предложена модифицированная математическая модель решаемой задачи, разработан эффективный алгоритм ACР-VP_М на базе алгоритма муравьиной колонии, основанного на популяции и эволюционной стратегии (1,4)-ЕА, учитывающий различные ограничения, предоставленные компанией. В настоящее время алгоритм ACР-VP_М апробируется на реальных данных компании, занимающейся производством и доставкой химической продукции в различные регионы России, с целью сокращения общих стоимостных затрат.
Работа поддержана грантом РФФИ 18-07-00193-а.



