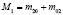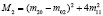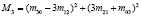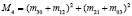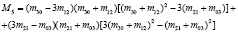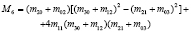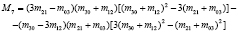В последнее время наблюдается повышение интереса к задачам распознавания образов в информатике, космосе, биомедицине и других приложениях. Об актуальности этого научного направления свидетельствует создание Национального комитета при Президиуме РАН по распознаванию образов и анализу изображений (НК РОАИ) [1]. Исследования по распознаванию образов приобретают крупномасштабный и международный характер в виде проводимых российских и международных конкурсов. Одним из перспективных направлений в области распознавания образов являются разработка, исследование и практическое применение характеристик, инвариантных к различным группам преобразований, что подчеркивается рядом актуальных современных публикаций [2–4].
В плоском случае инвариантами к операции поворота изображения некоторого объекта являются: площадь и длина контура изображения, отношение максимального и минимального расстояний от центра до границы объекта и другие особенности. В работах [5, 6] предложен и исследован способ сравнения профилей летательных объектов по габаритным параметрам. В сочетании с методами выделения объектов на фоне алгоритм может быть использован, например, для оценки относительного положения и распознавания движущихся объектов.
Представляет интерес направление, связанное с выделением инвариантов к яркостным и аффинным преобразованиям, что увеличивает вероятность получения правильного решения при распознавании образов.
В работах [7, 8] были предложены инвариантные моменты для бинарных и полутоновых изображений. Теоретическая и экспериментальная проверка инвариантности была выполнена, например, в работах [9, 10]. Отмечается, что на практике изображения зашумлены и нестабильны. В таких условиях уместно говорить о «псевдоинвариантах», которые чувствительны к деформациям и шумам, но являются инвариантами при отсутствии возмущающих факторов. Для создания классов образов необходимо иметь представительный набор графических изображений, составляющих обучающую выборку.
В настоящей работе исследуются свойства инвариантов изображений, в том числе анализируется их устойчивость к аффинным и яркостным преобразованиям. Обобщаются результаты практических исследований, проведенных автором и его коллегами применительно к задачам распознавания лиц, печатных символов и ригидных объектов на снимках ДЗЗ в ИПС им. А.К. Айламазяна РАН, ФИЦ ИУ РАН и РУДН в разное время.
Материалы и методы исследования
Теория алгебраических инвариантов работает с функциями классов, которые остаются неизменными даже при координатных трансформациях, и позволяет дать математическое обоснование инвариантных особенностей. Приведем некоторые определения применительно к графическим объектам [10–12].
Определение 1. Инвариантом называется функционал I(F), определенный на изображении F таким образом, что I(F) = I(D(F)) для пространства всех допустимых преобразований D, причем I(F1), I(F2) должны быть «достаточно различны» для разных изображений F1 и F2. Наиболее ценными дескрипторами служат геометрические и яркостные инварианты.
Определение 2. Моментами 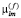 изображения f(x, y) называются отображения кусочно-непрерывной функции в полиномиальный базис,
изображения f(x, y) называются отображения кусочно-непрерывной функции в полиномиальный базис, 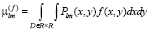 , где P – множество многочленов, определенных на компактном носителе
, где P – множество многочленов, определенных на компактном носителе 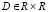 ; l, m – неотрицательные целые; r = l + m является порядком момента.
; l, m – неотрицательные целые; r = l + m является порядком момента.
Определение 3. Инвариантными моментами называются дескрипторы M1(f), ..., Mn(f), построенные на основе степенных моментов, которые описывают математическую модель изображения f(x, y) и являются инвариантами к его аффинным преобразованиям.
Примером служат инвариантные моменты, представленные в работе [7]. Вследствие дискретности цифровых изображений применение аффинных преобразований может приводить к частичной или полной потере свойств инвариантности (флуктуации моментов). Поэтому применительно к реальным изображениям следует говорить о «субинвариантах».
Определение 4. Субинвариантными моментами цифрового изображения F называются моменты M(F), величины которых могут меняться при выполнении аффинных преобразований. При этом они не должны превышать установленные допустимые величины отклонений Δ, приемлемые для решения задачи классификации.
В дальнейшем для удобства, там, где это не оговорено особо, будем называть инвариантные и субинвариантные моменты просто моментами.
Применение геометрических инвариантов в виде моментов не требует совмещений и масштабирования объектов, но они чувствительны к изменениям яркости.
Пусть дана функция f(x, y), а также моменты порядка не выше чем p + q, которые определены как:
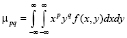 .
.
Если функция f(x, y) является кусочно-непрерывной и имеет нулевые значения только на ограниченной части образа, то существуют моменты μpq всех порядков, которые взаимно однозначно ее определяют.
Центральные моменты для цифрового изображения определяются следующим образом [8]:
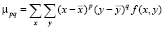 , (1)
, (1)
где 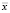 ,
, 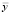 – это «центр тяжести» изображения.
– это «центр тяжести» изображения.
Нормализованные центральные моменты определяются так:
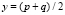 ,
, 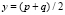 .
.
Центральные моменты позволяют найти семь инвариантных моментов (табл. 1). В работе [9] выполнен анализ чувствительности инвариантных моментов.
Таблица 1
Моменты и их чувствительности
|
Моменты |
Чувствительность к изменению масштаба |
Чувствительность к изменению яркости |
|
|
δ2 |
k |
|
|
δ4 |
k2 |
|
|
δ6 |
k3 |
|
|
δ6 |
k2 |
|
|
δ12 |
k2 |
|
|
δ4 |
k3 |
|
|
δ12 |
k2 |
Точность измерения координат точек объекта обозначим величиной δ, 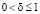 . Пусть
. Пусть 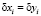 – возможные изменения (флуктуации) переменных
– возможные изменения (флуктуации) переменных 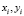 , вызванные ошибками измерений. С учетом этих ошибок центральный момент μ11 будет вычислен как:
, вызванные ошибками измерений. С учетом этих ошибок центральный момент μ11 будет вычислен как:
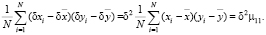
Отсюда следует, что чувствительность μ11 к изменениям данных пропорциональна или равна δ2. Результаты исследований теоретической чувствительности моментов представлены в табл. 1. Нетрудно убедиться в том, что моменты для полутоновых объектов чувствительны к изменениям освещенности. Нестабильность может привести к снижению показателей качества распознавания. Рассмотрим подходы к устранению этого недостатка.
Один из распространенных подходов связан с отказом от полутоновых изображений путем перехода к бинарным изображениям на основе пороговой фильтрации. Однако при этом может быть потеряна часть информации.
Другой подход связан с введением нормирования изображений, препятствующего изменениям яркостных представлений одного и того же объекта. Пусть яркостные характеристики изображения подвергаются линейному преобразованию 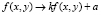 .
.
Подставим модифицированную яркость пикселей в формулу (1):
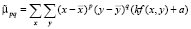 . (2)
. (2)
Для удобства перенумеруем все пиксели изображения по порядку:
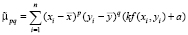 .
.
Тогда получим:
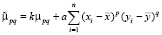 .
.
Откуда:
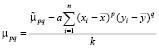 .
.
Центральные моменты, вычисленные по этим формулам, будут инвариантны к линейным преобразованиям яркости. В случае когда имеет место только мультипликативное изменение яркости, нормализация моментов не представляет затруднений. Однако на практике информация о параметрах яркостных преобразований часто является априори неизвестной. В табл. 1 представлена чувствительность 2D-инвариантных моментов к изменениям масштаба в δ раз и яркости изображения в k раз.
В качестве δ можно использовать величину, характеризующую размер изображения: 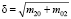 . С ее помощью можно построить моменты, инвариантные к масштабированию бинарных изображений [9].
. С ее помощью можно построить моменты, инвариантные к масштабированию бинарных изображений [9].
Результаты исследования и их обсуждение
Экспериментальные исследования проводились для объектов разной природы, включая фотографии лиц, буквы алфавита и профили самолетов. При этом в качестве признаков использовались инвариантные моменты, а в качестве классификаторов для распознавания объектов применялись метрики Евклида и Евклида–Махаланобиса.
Распознавание лиц метрикой Евклида
Для проведения серии экспериментов по распознаванию лиц был применен метод инвариантных моментов в сочетании с метрикой Евклида. В качестве объектов исследования использованы фотографии из открытой базы данных – 30 человек с разрешением 320x420 пикселей. Рассмотрим примеры распознавания лиц в условиях, когда они могут быть представлены в различных ракурсах. В табл. 2 представлены некоторые образцы фотографий.
Целесообразно осуществить переход от цветных изображений к полутоновому виду, воспользовавшись следующей формулой: 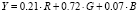 . Без потери общности положим, что изображения в базах данных приведены к одному масштабу.
. Без потери общности положим, что изображения в базах данных приведены к одному масштабу.
В табл. 3 представлены инвариантные моменты для первых образцов (первого столбца) табл. 2.
В табл. 4 представлены расстояния Евклида 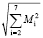 между экземплярами, причем первый момент ввиду большой абсолютной величины в расчет не брался.
между экземплярами, причем первый момент ввиду большой абсолютной величины в расчет не брался.
Точность распознавания с применением метрики Евклида составила около 80 %.
Таблица 2
Фрагмент базы данных с фотографиями
|
Образец 1 |
|
|
|
|
Образец 2 |
|
|
|
|
Образец 3 |
|
|
|
|
Образец 4 |
|
|
|
|
Образец 5 |
|
|
|
|
Образец 6 |
|
|
|
|
Образец 7 |
|
|
|
С целью расширения исследований и повышения достоверности решалась задача распознавания образов с применением метрик на существенно большем числе экземпляров. При этом допускались изменения в расположении лица на фотографии, наклоны головы, небольшие повороты, плохая освещенность.
Распознавание лиц с применением расстояния Евклида–Махаланобиса
Классы распознаваемых объектов могут пересекаться по установленной мере близости. С целью улучшения качества распознавания была введена мера Махаланобиса [11].
Таблица 3
Значения моментов для первого столбца
|
Образец |
М1 |
М2 |
М3 |
М4 |
М5 |
М6 |
М7 |
|
1 |
108,87 |
8,09 E-2 |
7,70 E-3 |
1,25 E-4 |
7,00 E-8 |
1,59 E-6 |
1,01 E-7 |
|
2 |
97,05 |
0,96 E-1 |
6,32 E-3 |
3,04 E-4 |
–8,3 E-7 |
7,22 E-6 |
1,18 E-7 |
|
3 |
93,12 |
9,77 E-2 |
5,87 E-3 |
6,05 E-4 |
3,63 E-7 |
–5,13 E-5 |
–3,41 E-8 |
|
4 |
105,13 |
1,00 E-1 |
4,90 E-3 |
9,95 E-5 |
–1,09 E-7 |
8,72 E-5 |
6,55 E-7 |
|
5 |
99,60 |
0,91 E-1 |
7,15 E-3 |
3,98 E-4 |
–2,67 E-7 |
–4,52 E-5 |
–4,90 E-7 |
|
6 |
104,54 |
0,95 E-1 |
6,83 E-3 |
6,22 E-4 |
6,14 E-7 |
–2,74 E-5 |
7,18 E-8 |
|
7 |
102,17 |
1,07 E-1 |
8,04 E-3 |
2,72 E-4 |
–9,66 E-8 |
–6,8 E-6 |
–1,25 E-7 |
Таблица 4
Расстояния Евклида между образами
|
Образец |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
0 |
2.67E-03 |
3.00E-03 |
3.46E-03 |
1.74E-03 |
2.48E-03 |
4.90E-03 |
|
2 |
2,67E-03 |
0 |
3.29E-04 |
7.84E-04 |
9.35E-04 |
1.91E-04 |
2.23E-03 |
|
3 |
3.00E-03 |
3.29E-04 |
0 |
4.55E-04 |
1.26E-03 |
5.20E-04 |
1.90E-03 |
|
4 |
3.46E-03 |
7.84E-04 |
4.55E-04 |
0 |
1.72E-03 |
9.75E-04 |
1.45E-03 |
|
5 |
1.74E-03 |
9.35E-04 |
1.26E-03 |
1.72E-03 |
0 |
7.44E-04 |
3.17E-03 |
|
6 |
2.48E-03 |
1.91E-04 |
5.20E-04 |
9.75E-04 |
7.44E-04 |
0 |
2.42E-03 |
|
7 |
4.90E-03 |
2.23E-03 |
1.90E-03 |
1.45E-03 |
3.17E-03 |
2.42E-03 |
0 |
Определение 5. Расстоянием Махаланобиса между двумя векторами 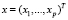 и
и 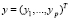 в пространстве Rp называют функцию вида:
в пространстве Rp называют функцию вида:
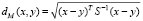 , (3)
, (3)
где S – матрица ковариации; 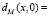
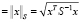 является нормой x.
является нормой x.
Все точки с одним и тем же расстоянием, имеющим норму 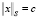 , удовлетворяют равенству
, удовлетворяют равенству 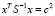 . Заметим, что если матрица ковариации S в функции
. Заметим, что если матрица ковариации S в функции 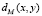 является единичной, то расстояние Махаланобиса становится равным расстоянию Евклида.
является единичной, то расстояние Махаланобиса становится равным расстоянию Евклида.
Для задачи классификации (принятие решения о принадлежности вектора классу) вводится расстояние Махаланобиса между вектором x и центром класса 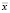 , которое определяется как
, которое определяется как 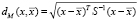 .
.
Метрика Махаланобиса обладает тем недостатком, что не может быть применена в случае обращения в нуль хотя бы одного элемента главной диагонали матрицы S, поэтому на практике используют ее модификации.
Определение 6. Расстоянием Евклида–Махаланобиса между двумя векторами 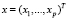 и
и 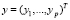 в пространстве Rp называется функция вида [11]:
в пространстве Rp называется функция вида [11]:
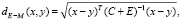 (4)
(4)
где E – единичная матрица. Метрика Евклида–Махаланобиса (4) устраняет недостаток метрики Махаланобиса (3), поскольку элементы ее главной диагонали всегда больше нуля.
Была проведена серия экспериментов, для которой использованы фотографии 168 человек с разрешением 180х200 пикселей из открытой базы данных [12], общим размером 3360 изображений. При этом 150 человек представлены вариантами лиц с незначительной мимикой и 18 человек – с сильными эмоциями.
В табл. 5 приведены примеры нескольких классов и тестовые примеры лиц людей с незначительными изменениями мимики. В таблице 6 приведены примеры фотографий плохого качества, на которых представлены люди с незначительным изменением мимики.
Применение метрики Евклида–Махаланобиса обеспечивает хорошее качество распознавания при небольших яркостных флуктуациях, она хорошо справляется с такими усложняющими распознавание факторами, как закрытые глаза, мимика (улыбки, гримасы и т.п.), наличие поворотов и наклонов головы. Точность распознавания с применением метрики Махаланобиса для первой группы составила 93,33 %, для второй – 89 %.
Распознавание букв алфавита метрикой Евклида
В подходе [13] предлагается выделять до 80 геометрических признаков с последующей статистической обработкой результатов и принятием наиболее вероятного решения. Заметим, что и статистические методы обеспечивают лишь 50–80 %-ное распознавание для рукописного текста. Работы по практическому распознаванию букв и текстов на их основе по-прежнему являются актуальными, о чем свидетельствуют многочисленные публикации и доклады на конференциях по распознаванию образов.
Подход к распознаванию символов с применением моментов является достаточно популярным. Укажем, например, работу [14], в которой рассматривается алгоритм формирования признаков и решающих правил распознавания символов на основе инвариантных моментов на базе модели описания бинарного растрового изображения.
Таблица 5
Примеры фотографий людей с незначительным изменением эмоций
|
Примеры из обучающих выборок |
Примеры для распознавания |
||||
|
Класс 1 |
|
|
|
Пример 1 |
|
|
Класс 2 |
|
|
|
Пример 2 |
|
|
Класс 3 |
|
|
|
Пример 3 |
|
Таблица 6
Примеры фотографий, на которых представлены лица людей с сильными эмоциями
|
Примеры из обучающих выборок |
Примеры для распознавания |
||||
|
Класс 1 |
|
|
|
Пример 1 |
|
|
Класс 2 |
|
|
|
Пример 2 |
|
|
Класс 3 |
|
|
|
Пример 3 |
|
В табл. 7 показаны буквы и соответствующие этим буквам значения критерия. Распознавание букв алфавита проводилось на примере шрифта Times New Roman. За эталон были взяты заглавные буквы от «А» до «Я». Кегль равнялся 80 pt, а максимальный размер поля, на котором могли рассматриваться обрабатываемые буквы, – 300x300 точек.
При написании букв крупным кеглем появляется эффект «бахромы». Здесь целесообразен переход к бинарному изображению, реализуемый пороговой фильтрацией.
Для малой буквы «А» (кегль = 50 pt) мера равна 0,70065, для большой – 0,72302 (кегль = 180 pt). Форма интерфейса для распознавания букв представлена на рис. 1.
В левой верхней части формы расположено рабочее поле размером 300х300 пикселей, что достаточно для распознавания буквы размером до 200 pt. Три числа вверху справа (3518 86482 90000) соответствуют количеству черных пикселей, нечерных пикселей и общему количеству пикселей. Форма содержит значения инвариантных моментов для данной буквы и аддитивную меру близости.
Точность распознавания в соответствии с аддитивной мерой достаточно высока и составляет примерно 90 %. Для повышения точности распознавания следует применить преобразования, связанные с утоньшением и устранением «бахромы». Логические методы выполнения подобных преобразований хорошо описаны в работе [15].
Распознавание летательных аппаратов (ЛА) по контурам
Задача классификации ЛА по габаритным параметрам в большинстве практически важных случаев может быть сведена к исследованию контура (проекции) [6].
Таблица 7
Мера Евклида для букв алфавита (фрагмент)
|
А |
Б |
В |
Г |
Д |
Е |
Ё |
Ж |
З |
И |
|
0,701 |
0,173 |
0,0494 |
0,601 |
0,245 |
0,166 |
0,311 |
0,006 |
0,363 |
0,001 |
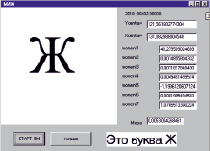
Рис. 1. Интерфейс для распознавания букв
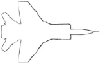
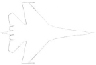
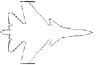
|
|
|
|
|
|
Миг-29 |
Миг-31 |
Су-27 |
Су 35-37 |
Рис. 2. Профили самолетов
Таблица 8
Значения инвариантных моментов для контуров самолетов
|
Тип летательного аппарата |
||||
|
Момент |
Миг-29 |
Миг-31 |
Су-27 |
Су-37 |
|
М1 |
44,117 |
106,886 |
45,200 |
44,980 |
|
М2 |
0,157 |
0,207 |
0,357 |
0,353 |
|
М3 |
0,759 |
0,382 |
0,740 |
0,409 |
|
М4 |
0,233 |
0,132 |
0,441 |
0,169 |
|
М5 |
0,097 |
0,028 |
0,252 |
0,044 |
|
М6 |
0,087 |
0,060 |
0,264 |
0,100 |
|
М7 |
0,013 |
0,010 |
–0,001 |
-0,000 |
|
Аддитивный критерий |
0,820 |
0,459 |
1,001 |
0,577 |
Таблица 9
Расстояния для тестовой выборки
|
Тип самолета |
Расстояние Евклида |
Расстояние Махаланобиса |
||
|
Класс «Миг» |
Класс «Су» |
Класс «Миг» |
Класс «Су» |
|
|
Миг-27 |
3,18 |
23,93 |
2,95 |
266,12 |
|
Су-39 |
1,43 |
0,06 |
4,49 |
0,87 |
В табл. 8 указаны инвариантные моменты из обучающей выборки.
Процесс идентификации летательного аппарата заключается в сравнении отдельных элементов или полных наборов инвариантных моментов исследуемого и эталонных изображений. В табл. 9 приведены классифицирующие расстояния для некоторых тестируемых типов ЛА.
Видно, что обе метрики правильно классифицируют тестируемые образцы.
Измерение расстояний при условии корректного выделения силуэта позволяет идентифицировать образцы с точностью свыше 90 %.
Заключение
Применение инвариантов в качестве признаков изображений в общем случае дает неплохие результаты по распознаванию объектов различной природы за счет некоторой устойчивости к небольшим флуктуациям и искажениям изображений. Это могут быть фотографии, символы, объекты ДЗЗ и др. Для распознавания образов возможно применение различных метрик и классификаторов. Этап выделения признаков является определяющим для эффективной классификации образов. Инварианты в качестве признаков осуществляют существенное сжатие информации о классах, однако способны в некоторых пределах обеспечивать устойчивость к возмущениям среды в задачах распознавания. Для реальных динамических изображений с целочисленными значениями координат моменты могут флуктуировать из-за геометрических искажений. При распознавании фотографий адекватной мерой является расстояние Махаланобиса и Евклида–Махаланобиса. Разработанную систему целесообразно использовать для классификации фотографий с изображениями лиц в сложных условиях: измененная мимика (улыбка и т.п.), повороты и/или наклоны головы, небольшие яркостные изменения (в пределах 20 %).
Работа выполнена при частичной финансовой поддержке проектов РФФИ № 20-07-00022 А «Разработка и исследование методов распознавания образов на основе инвариантов к яркостным и геометрическим преобразованиям в системах технического зрения беспилотных летательных аппаратов»; № 18-29-03011 мк «Исследование и разработка новых методов и технологий для задач интеллектуального анализа и оптимизации обработки больших потоков данных дистанционного зондирования Земли».