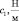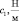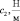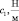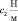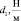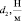Роторы, валы, балки и другие элементы являются частыми составляющими подвижных и неподвижных механических систем [1; 2]. Известно, что по акустическому отклику конструкций возможно восстановление различного рода неисправностей таких систем. Исследования, связанные с изношенностью, а также с изменениями физических параметров конструкций, играют важную роль при решениях проблем сохранения безопасных частот свободных колебаний [3; 4].
Действительно, частыми случаями на практике являются колебания, возникающие при отсутствии какого-либо внешнего периодического возбуждения. Это и сравнительно простые процессы свободных колебаний, возникающие после мгновенного нарушения состояния устойчивого равновесия механической системы, и более сложные процессы, такие как автоколебания систем.
Большое внимание исследователей в настоящее время привлечено к вопросам колебаний самых разнообразных механических конструкций (автомобилей, кораблей и самолетов, инженерных сооружений, роторов турбин, валов двигателей, турбинных лопаток, воздушных и гребных винтов, перекрытий промышленных зданий и т.п.).
Многие научные труды по теории колебаний включают задачи свободных колебаний валов, роторов, например работы [2; 5; 6]. Целью данной работы является построение динамической модели ротора, закрепленного податливыми подшипниками с различными жесткостями в горизонтальном и вертикальном направлениях, получение дифференциальных уравнений, описывающих колебательный процесс. В работе приводится также вывод векового уравнения прямой спектральной задачи. С помощью построенной программы по алгоритму решения задачи исследуется зависимость частот колебаний ротора от его физических параметров. Полученные результаты учитываются при обеспечении надежности механических колебательных процессов, составляющими которых являются роторы на податливых подшипниках.
Прямая задача определения частот свободных колебаний ротора на подшипниках
Смоделируем свободные колебания жесткого ротора, закрепленного подшипниками на податливых опорах.
Систему координат Oxyz совмещаем с ротором так, как представлено на рисунке. За обобщенные координаты принимаем угловые перемещения β, γ оси ротора, а также перемещения y0, z0 центра тяжести ротора и малые перемещения y1, z1, y2, z2 подшипников в направлениях осей Oy и Oz [2].
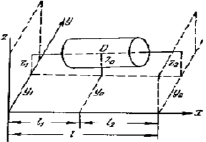
Модель ротора на податливых подшипниках
Здесь: W и J – масса ротора и момент инерции его поперечного сечения; с1, с2 и d1, d2 – коэффициенты жесткостей подвижных опор в горизонтальном и вертикальном направлениях соответственно; l1, l2 – расстояния от центра тяжести ротора до его податливых опор, причем l1 + l2 = l.
По такой динамической модели для центра тяжести и угловых перемещений имеем равенства:
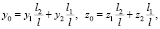
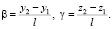
Тогда соответствующие дифференциальные уравнения перемещений центра тяжести ротора и его поворотов относительно указанных осей примут вид:
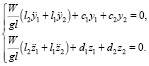
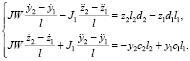(1)
Четыре уравнения системы (1) описывают моделируемый колебательный процесс.
Вывод векового уравнения прямой задачи
С учетом свободных колебаний жесткого ротора на нежестких опорах принимаем колебательный процесс гармоническим:
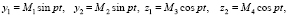(2)
где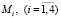 
– амплитуды, p – собственная частота колебаний ротора.
Тогда с учетом (2) уравнения (1) примут вид
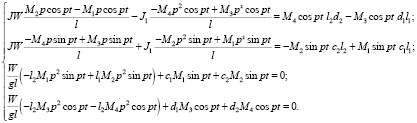
Преобразуя последнюю систему, определяем четыре однородных уравнения относительно амплитуд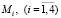 
колебаний ротора.
Далее с учетом существования ненулевого решения этой системы [7] найдем вековой определитель для нашей задачи в виде:
.
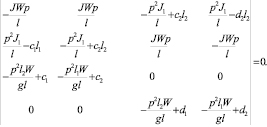Преобразования определителя приводят его к уравнению восьмого порядка относительно частоты колебаний
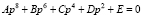. (3)
с коэффициентами, содержащими в себе физические параметры жесткого ротора и податливых подшипников:
.
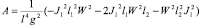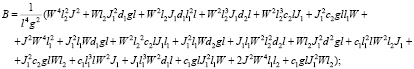
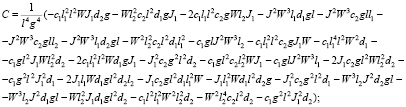(4)
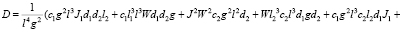
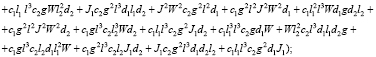
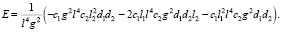
Вековое уравнение (3)–(4) позволяет находить частоты нормальных форм колебаний жесткого ротора, закрепленного подшипниками на податливых опорах.
Применение математической модели (3)–(4) представим на примере. Пусть известны физические параметры ротора на подвижных опорах: J = 0,5 кг м2, l = 0,3 м,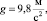 
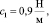
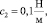W = 2 кг,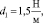 
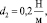J1 = 0,25 кг•м2, l1 = 0,1 м, l2 = 0,2 м.
Определим собственные частоты колебаний ротора.
Подстановка заданных физических параметров ротора и подшипников в (4), а затем в (3) приводит к уравнению:
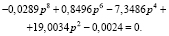
Решение последнего уравнения, найденное с помощью программы в математическом пакете Maple, следующее: ±0,011, ±2,211, ±2,881, ±4,022.
Следовательно, собственные частоты колебаний ротора, соответствующие заданным характеристикам:
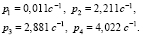
Полученная по алгоритму решения прямой задачи программа подтверждает также четырехчастотный колебательный процесс, полученный при его математическом и физическом моделировании.
Зависимость частот колебаний ротора на подшипниках от физических параметров
Рассмотрим теперь с помощью полученной математической модели (3), (4) влияние характеристик ротора на значения собственных частот его колебаний.
Даны следующие параметры ротора и подшипников:
J = 0,5 кг м2, l = 0,3 м,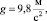 
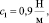
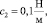W = 2 кг,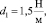 
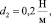
J1 = 0,25 кг•м2, l1 = 0,1 м, l2 = 0,2 м. (5)
Для исследований меняем какие-либо физические характеристики (например, массу ротора), оставляя другие характеристики постоянными. И с помощью модели (3), (4) будем определять соответствующие изменения в частотном спектре задачи.
Проведенные с помощью программы Maple расчеты показывают уменьшение частот колебаний при увеличении массы ротора или момента инерции поперечного его сечения. Это можно увидеть, например, в табл. 1.
Таблица 1
Зависимость частот от массы ротора при его параметрах (5)
|
W, кг |
р1, с-1 |
р3, с-1 |
|
2 |
0,011 |
2,881 |
|
3 |
0,007 |
1,806 |
|
4 |
0,005 |
1,565 |
|
5 |
0,004 |
1,399 |
|
6 |
0,003 |
1,345 |
Расчеты влияния на значения частот колебаний ротора жесткостей его подвижных опор показывают, что здесь образуется прямая зависимость: увеличение параметров жесткости ведет к увеличению частот колебаний. Результаты вычислений представлены, например, табл. 2, 3.
Таблица 2
Зависимость частот от коэффициента жесткости податливых подшипников в горизонтальном направлении (при параметрах (5) ротора)
|
|
р1, с-1 |
р2, с-1 |
|
0,2 |
0,011 |
1, 399 |
|
0,6 |
0,014 |
1,979 |
|
1 |
0,015 |
2,423 |
|
1,4 |
0,015 |
2,795 |
|
1,8 |
0,016 |
2,998 |
Таблица 3
Зависимость частот ротора от коэффициентов жесткости в горизонтальном направлении при параметрах (5) ротора
|
|
|
р1, с-1 |
р2, с-1 |
|
0,100 |
0,100 |
0,0084 |
0,9898 |
|
0,500 |
0,500 |
0,0188 |
1,2126 |
|
1,100 |
1,100 |
0,0278 |
2,8810 |
|
2,000 |
2,000 |
0,0373 |
2,8813 |
|
2,400 |
2,400 |
0,0412 |
2,8815 |
Проведенные расчеты показывают также, что одновременное увеличение жесткостей подвижных опор ротора (как в горизонтальном, так и в вертикальном направлениях) приводит к более значительному росту значений частот, чем при увеличении только в одном направлении. В подтверждение сказанного приведена табл. 4.
Таблица 4
Зависимость частот колебаний от коэффициентов жесткостей опор в горизонтальном и вертикальном направлениях при параметрах (5) ротора
|
|
|
|
|
р1, с-1 |
р2, с-1 |
р3, с-1 |
|
0,1 |
0,1 |
0,1 |
0,1 |
0,004 |
0,989 |
0,991 |
|
0,6 |
0,6 |
0,6 |
0,6 |
0,026 |
2,421 |
2,425 |
|
1 |
1 |
1 |
1 |
0,044 |
3,119 |
3,131 |
|
2 |
2 |
2 |
2 |
0,088 |
4,039 |
4,429 |
|
2,8 |
2,8 |
2,8 |
2,8 |
0,112 |
4,143 |
4,502 |
Аналогичные зависимости влияния характеристик масс и жесткостей на частотный спектр наблюдаются и при других физических характеристиках механической системы, отличных от (5).
Заключение
Рассмотрена прямая задача малых свободных колебаний ротора на подвижных опорах. Построены дифференциальные уравнения перемещений центра тяжести ротора и его поворотов относительно осей по двум подвижным направлениям. По динамической модели найдено вековое уравнение задачи с определением частот нормальных форм колебаний.
С помощью векового уравнения исследовано влияние на частоты колебаний ротора его физических параметров. Построены зависимости при различных характеристиках ротора и подшипников. Показано, что увеличение параметров жесткости увеличивает значения частот, а увеличение массовых параметров – уменьшает значения частот колебаний. Проведенные исследования учитываются при решении проблем диагностики технических конструкций, связанных с изменениями в физических параметрах различного вида роторных конструкций.
Результаты исследований могут представить как теоретический, так и практический интерес при определении частот колебаний любого ротора на нежестких опорах. Причем как на этапах доводки, проектирования двигателей (насосов, осевых и центробежных компрессоров) машиностроения, так и на этапах практических спектральных расчетов.