В последнее десятилетие наблюдается тенденция по расширению сферы применения низкоорбитальных систем спутниковой связи (НССС). Невозможно представить себе без НССС развитие Северного морского пути, развертывание подразделений Вооруженных сил Российской Федерации, обеспечивающих безопасность страны в Арктике, а также создание глобальной многофункциональной инфокоммуникационной спутниковой системы [1; 2]. Очевидно, что современные НССС должны обладать высокой информационной скрытностью. В работах [3; 4] для достижения данной цели предлагается использовать систему опознавания «свой-чужой». С целью повышения скорости опознавания спутников НССС в работе [5] предлагается использовать полиномиальные модулярные коды (ПМК), которые обеспечивают параллельную реализацию протокола аутентификации. Однако при введении избыточности полиномиальные модулярные коды могут осуществлять поиск и коррекцию ошибок, что позволит повысить отказоустойчивость системы опознавания «свой-чужой». Поэтому разработка алгоритма коррекции результатов вычислений с помощью ПМК является актуальной задачей.
Для повышения эффективности функционирования системы опознавания спутников предлагается воспользоваться непозиционными полиномиальными модулярными кодами, в которых данные, представленные в виде набора остатков, обрабатываются параллельно. Так как в процессе вычислений обмена между основаниями не происходит, то данное свойство используется для построения кодов, способных осуществлять поиск и коррекцию ошибок. Поэтому целью работы является разработка алгоритма коррекции ошибок в ПМК, применение которого позволит повысить отказоустойчивость системы «свой-чужой».
Материалы и методы исследования
Чтобы получить полиномиальный модулярный код, выбирают кортеж неприводимых полиномов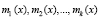 
[6; 7]. Их произведение дает рабочий диапазон
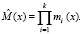(1)
Тогда полином Y(x) можно однозначно описать комбинацией ПМК
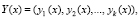(2)
где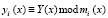 
; 
; 
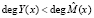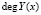– степень полинома Y(x).
При этом для арифметических операций, выполняемых в ПМК, справедливо
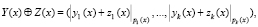(3)
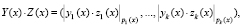(4)
где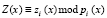 
; i = 1, 2, ..., k; 
.
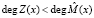В работе [5] представлен протокол аутентификации спутника, реализованный в ПМК. Выбираем параметры, удовлетворяющие условию
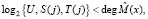(5)
где U – секретный ключ спутника, S(j) и T(j) – сеансовый ключ и число, позволяющее определить повторное использование данного ключа.
Представляем их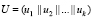 
, 
, 
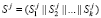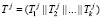, где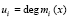 
, 
; 
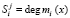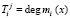; i = 1, 2, ..., k.
1. Перед j-м сеансом связи ответчик определяет истинный статус спутника в ПМК
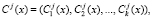(6)
где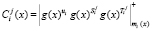 
; 
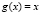; i = 1, 2, ..., k.
2. Затем производится изменение секретных параметров
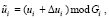
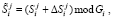
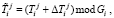(7)
где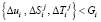 
– случайные числа; 
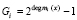; i = 1, 2, ..., k.
3. После вычисляется зашумленный статус спутника, используя ПМК
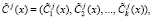(8)
где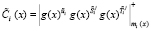 
.
4. Для опознавания запросчик задает вопрос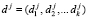 
, где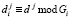 
.
5. Ответчик, находящийся на спутнике, отвечает на вопрос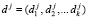 
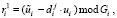
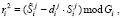
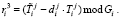(9)
6. Ответчик осуществляет передачу запросчику следующих данных
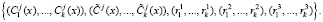
7. Запросчик осуществляет проверку статуса спутника
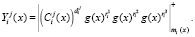(10)
Статус «свой» будет только при выполнении условия
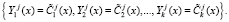(11)
Анализ выражений (5)–(11) показывает, что применение ПМК позволило сократить время опознавания. При этом ПМК способны осуществлять поиск и исправление ошибок [7]. Так, для исправления однократной ошибки необходимо два основания, так чтобы
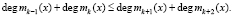(12)
В результате этого получаем полный диапазон избыточного ПМК
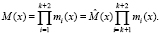(13)
Комбинация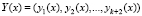 
не содержит ошибки, если
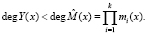(14)
Однократная ошибка изменяет значение j-го остатка согласно
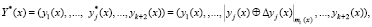(15)
где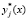 
– искаженный остаток ПМК; 
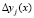– глубина однократной ошибки.
В результате нарушается условие (14), так как имеем
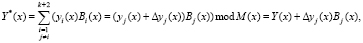(16)
где Bi(x) – ортогональные базисы ПМК;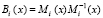 
; 
.
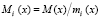Для поиска и коррекции ошибок в полиномиальных модулярных кодах в работе [7] рекомендуется вычислять позиционную характеристику – интервал ПМК
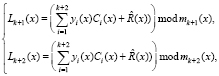(17)
где 
; 
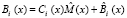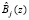и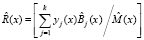 
– ортогональный базис и ранг кортежа информационных оснований ПМК.
С целью снижения схемных затрат был разработан алгоритм, позволяющий определить место и величину ошибки на основе модульной свертки.
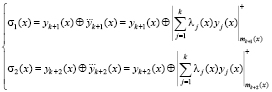, (18)
где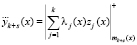 
– модульная свертка; λj(x) – константа свертки; s = 1,2.
Для вычисления констант модульной свертки воспользуемся китайской теоремой об остатках (КТО) для безызбыточной системы полиномиального модулярного кода, то есть
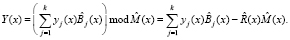(19)
Известно, что ортогональный базис определяется
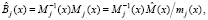(20)
где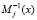 
– вес ортогонального базиса.
Чтобы определить константу свертки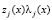 
, где j = 1, 2, ..., k, необходимо найти 
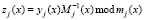, при этом 
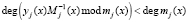В этом случае при реализации (19) можно отказаться от вычисления ранга, то есть имеем
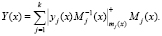(21)
Тогда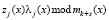 
, где j = 1, 2, ..., k, s = 1, 2., определяется
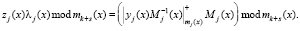(22)
Значит, модульная свертка позволяет корректировать ошибку в ПМК, используя
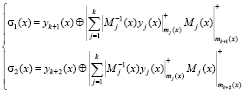(23)
Если свертка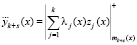 
совпадает с контрольным основанием, то комбинация ПМК не содержит ошибки. В противном случае – комбинация ПМК ошибочная.
Результаты исследования и их обсуждение
В качестве информационных оснований ПМК выбираем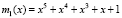 
, 
, 
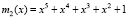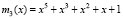. Согласно (1) рабочий диапазон 
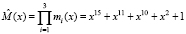. Согласно (12) контрольными основаниями ПМК будут 
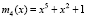и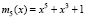 
. Используя (21), определим
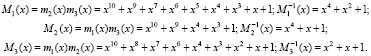
Для выполнения алгоритма поиска и коррекции ошибки вычислим константы
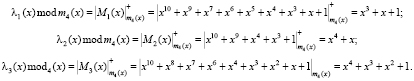
Для второго контрольного основания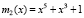 
имеем константы
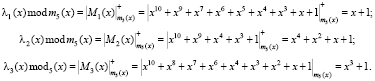
Выбираем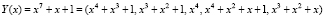 
. Вычислим произведение 
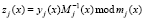, где j = 1, 2, 3. Тогда
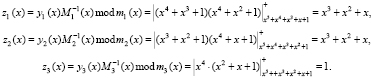
Воспользуемся модульной сверткой и вычислим контрольные остатки
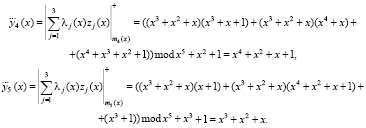
Тогда согласно (18) получаем, что комбинация не содержит ошибки, так как
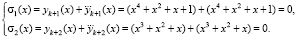
Введем ошибку, равную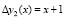 
. Тогда 
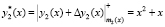, а комбинация ПМК примет вид 
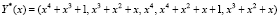. Вычислим остатки по контрольным основаниям
.
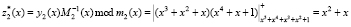Воспользуемся модульной сверткой и вычислим контрольные остатки
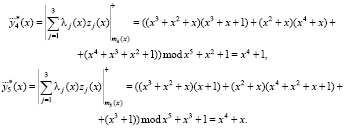
Тогда согласно (18) получаем, что комбинация содержит ошибки, так как
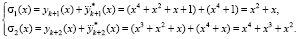
На основании результата выбираем вектор ошибки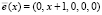 
. Тогда
.
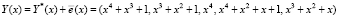Используя рассмотренный алгоритм, разработали структурную схему устройства поиска и коррекции ошибки. Произведем оценку схемных затрат на реализацию разработанного алгоритма. Устройство содержит два тракта, в каждом из которых:
– три LUT-таблицы, реализующие вычисление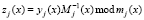 
;
– три LUT-таблицы, реализующие вычисление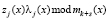 
;
– две LUT-таблицы, реализующие вычисление модульной свертки.
Значит, на устройство поиска и коррекции ошибки, использующее модульную свертку, необходимо 16 LUT-таблиц.
В этом случае устройство, реализующее алгоритм поиска и коррекции ошибок, определяемый (14), также содержит два тракта, в каждом из которых:
– пять LUT-таблиц, реализующих вычисление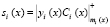 
;
– четыре LUT-таблицы, реализующие вычисление ранга ПМК;
– три LUT-таблицы, реализующие вычисление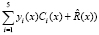 
.
Значит, на устройство поиска и коррекции ошибки, построенное на основе алгоритма [7], необходимо 22 LUT-таблицы. Таким образом, разработанный алгоритм позволяет сократить аппаратные затраты в 1,375 раза по сравнению с использованием алгоритма вычисления интервала ПМК.
Заключение
С целью сокращения времени, необходимого на определение статуса космического аппарата, был предложен протокол аутентификации, реализованный в ПМК. При этом полиномиальные модулярные коды позволяют обнаруживать и исправлять ошибки, которые возникают в процессе функционирования системы опознавания, что позволит повысить ее отказоустойчивость. В работе показан алгоритм поиска и коррекции ошибок в полиномиальных кодах, который базируется на использовании модульной свертки. Проведенные исследования показали, что при использовании полиномов пятой степени разработанный алгоритм требует в 1,375 раза меньше аппаратных затрат по сравнению с алгоритмом вычисления интервала ПМК, приведенным в работе [7].
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-07-01020.