Важную роль в процессе изучения вычислительной техники играет практическая подготовка. Самостоятельная разработка простейших узлов и блоков ЭВМ с последующим построением и экспериментальным исследованием их программных моделей на занятиях в компьютерном классе способствует более глубокому усвоению изучаемого материала. Программные модели исследуемых узлов и блоков могут создаваться с помощью различных инструментальных средств [1–3] или представлять собой готовые программы [4]. Развитие технологий использования в учебном процессе программных моделей узлов и блоков ЭВМ является актуальной задачей, так как способствует повышению эффективности обучения.
Цель исследования: развитие технологии построения и использования действующих функциональных моделей применительно к узлам и блокам ЭВМ, содержащим память (являющимся последовательностными схемами), на основе табличного процессора Microsoft Excel при проведении практических занятий в компьютерном классе.
В технологии построения действующих функциональных моделей узлов и блоков ЭВМ при проведении практических занятий на компьютере с использованием табличного процессора Microsoft Excel, ориентированной на комбинационные схемы, выделяются следующие этапы [5]: анализ задания по разработке функциональной модели; описание работы узла (блока) с помощью формул булевых функций; разработка схемы; разработка экранной формы для экспериментального исследования; построение функциональной модели; экспериментальные исследования функциональной модели; оформление отчета по результатам работы.
Переход от моделирования комбинационных схем к последовательностным схемам вносит изменения в содержание этапов технологии построения действующих функциональных моделей узлов и блоков ЭВМ с использованием табличного процессора Microsoft Excel, обусловленные особенностью функционирования последовательностных схем. Эта особенность проявляется в зависимости выходного сигнала не только от поступивших в данный момент на входы значений логических переменных, но и от тех значений переменных, которые поступали на входы в предыдущие моменты времени. Для выполнения этого условия значения переменных должны запоминаться узлом (блоком). Функцию запоминания значений логических переменных в последовательностных узлах и блоках выполняют элементы памяти, представляющие собой триггеры, способные под воздействием входных сигналов переходить в одно из двух устойчивых состояний и сохранять это состояние при отсутствии входных сигналов.
Возможность моделирования последовательностных схем в Microsoft Excel
Электронные таблицы Microsoft Excel в обычном режиме работы хорошо подходят для моделирования комбинационных схем, так как в электронной таблице, как и в комбинационной схеме, изменения значений входных переменных автоматически приводят к изменению (пересчету) значений выходных переменных. Поскольку значения выходных переменных в электронной таблице зависят только от значений входных переменных, моделирование последовательностных схем оказывается невозможным.
Между тем моделирование последовательностных схем с помощью электронных таблиц Microsoft Excel становится возможным, если отказаться от автоматического вычисления формул при изменении значений входных переменных. Для этого необходимо изменить параметры Microsoft Excel, связанные с вычислением формул (Файл/Параметры/Формулы/Параметры вычислений/Вычисления в книге/вручную) (рис. 1).
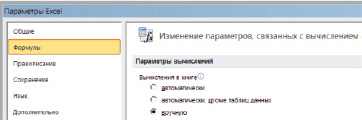
Рис. 1. Изменение параметров вычисления формул
В результате будет отключен режим автоматических вычислений и включен режим ручных вычислений, в котором для выполнения пересчета формул необходимо нажимать клавишу F9 (или выбирать команду «Пересчет»). При моделировании узлов и блоков клавиша F9 будет выполнять функции клавиши «Такт».
Моделирование триггеров с помощью табличного процессора Microsoft Excel
Ячейка листа Microsoft Excel может выступать в качестве элемента памяти, значения входных сигналов которого содержатся в других ячейках, а работа элемента памяти описывается формулой, занесенной в соответствующую ему ячейку. Новое состояние элемента памяти, зависящее от текущего состояния и значения входных сигналов, формируется после пересчета формулы в соответствующей элементу памяти ячейке при нажатии клавиши F9.
Таким образом, ячейка листа Microsoft Excel позволяет моделировать функционирование простейших последовательностных схем – триггеров. Поскольку изменение состояния триггера происходит под действием специального сигнала, вырабатываемого при нажатии клавиши «Такт», то моделируется работа синхронных триггеров.
Пример синхронного D триггера приведен на рис. 2, где представлено условное графическое изображение (УГО), а также таблица переходов и функция переходов, описывающие функционирование триггера. При отсутствии сигнала синхронизации C (C = 0) состояние Q триггера в момент времени (t + 1) совпадает с состоянием в предыдущий момент времени (t): Q(t + 1) = Q(t). При поступлении сигнала синхронизации C (C = 1) триггер в момент времени (t + 1) переходит в состояние, определяемое информационным входом D: Q(t + 1) = D.
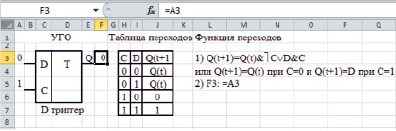
Рис. 2. Моделирование синхронного D триггера
При моделировании триггера на листе Microsoft Excel состояние триггера Q представляется содержимым ячейки F3, а сигнал на информационный вход D поступает из ячейки A3. При этом моделирование сигнала синхронизации не связано с содержимым ячеек листа Microsoft Excel и реализуется путем нажатия на клавиатуре компьютера клавиши «Такт» (F9). Принимая во внимание особенность моделирования сигнала синхронизации, а также то, что при отсутствии этого сигнала (C = 0) состояние последовательностных схем не изменяется, для упрощения логических формул далее используются формулы, описывающие работу схем при наличии сигнала синхронизации (C = 1).
Моделирование триггеров осуществляется путем построения формул функций перехода с последующей их реализацией в виде логических функций Microsoft Excel. Для получения формул функций перехода по словесному описанию работы триггеров могут быть использованы таблицы или графы переходов. На рис. 3 приведены примеры моделей трех типов триггеров: RS, DV и T (с установкой в нулевое состояние).
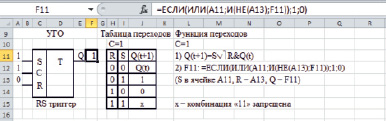
а)
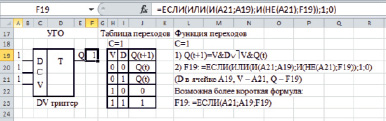
б)
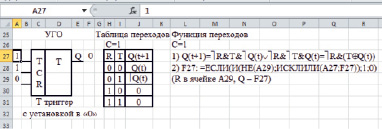
в)
Рис. 3. Модели триггеров: RS (а), DV (б) и T (в)
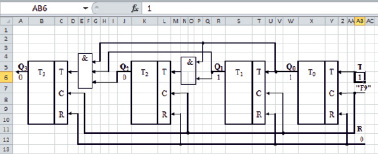
Рис. 4. Экранная форма функциональной модели 4-разрядного двоичного суммирующего счетчика
Для экспериментального исследования работы триггера после ввода логических формул, описывающих его работу, необходимо задать в ячейках, соответствующих входам, значения входных сигналов и нажать клавишу «Такт» (F9). Например, Т триггер при R = 0 и T = 1 при каждом нажатии на клавишу «Такт» переключается в противоположное состояние.
Моделирование счетчика с помощью табличного процессора Microsoft Excel
Моделирования узла с памятью рассмотрим на примере накапливающего счетчика. Счетчик может быть построен на основе рассмотренного выше Т триггера с установкой в «0». Пример схемы 4-разрядного двоичного суммирующего счетчика, моделируемого на листе Microsoft Excel, приведен на рис. 4.
Функциональная модель счетчика описывается формулами булевых функций и соответствующими им логическими формулами Microsoft Excel, приведенными в табл. 1.
Таблица 1
Описание функционирования счетчика
|
Формула булевой функции |
Лист Microsoft Excel |
|
|
Адрес ячейки |
Формула |
|
|
Q0(t + 1) = ?R&(Q0(t)⊕T) |
W6 |
= ЕСЛИ(И(НЕ(Z11);ИСКЛИЛИ(W6;Z6));1;0) |
|
Q1(t + 1) = ?R&(Q1(t)⊕Q0(t)) |
R6 |
= ЕСЛИ(И(НЕ(Z11);ИСКЛИЛИ(R6;W6));1;0) |
|
Q2(t + 1) = ?R&(Q2(t)⊕(Q1(t)&Q0(t)) |
J6 |
= ЕСЛИ(И(НЕ(Z11);ИСКЛИЛИ(J6;И(R6;W6)));1;0) |
|
Q3(t + 1) = ?R&(Q3(t)⊕(Q2(t)&Q1(t)&Q0(t)) |
A6 |
= ЕСЛИ(И(НЕ(Z11);ИСКЛИЛИ(A6;И(J6;R6;W6)));1;0) |
В моделируемом счетчике используются три комбинации управляющих сигналов: R = 1 – обнуление счетчика; R = 0 и T = 1 – счет; R = 0 и T = 0 – хранение текущего значения счетчика. Если тактовый сигнал, подаваемый с помощью клавиши F9, поступает при R = 1 (содержимое ячейки AB12 Microsoft Excel равно единице), то все триггеры счетчика устанавливаются в нулевое состояние. Если тактовый сигнал поступает при R = 0 и T = 1, то содержимое счетчика увеличивается на единицу.
Необходимо отметить особенность моделирования последовательностных схем с помощью табличного процессора Microsoft Excel, которая обусловлена порядком пересчета формул в ячейках электронной таблицы после нажатия клавиши F9. Пересчет формул в ячейках производится слева направо, сверху вниз. Это означает, что в счетчике на рис. 4 в начале будет вычислено значение старшего разряда (Т3), а затем последовательно разрядов Т2, Т1, Т0. Несмотря на такой порядок формирования новых значений разрядов, счетчик работает корректно, поскольку используется параллельное формирование переносов. При моделировании счетчика (сумматора) с последовательным переносом ячейки электронной таблицы, соответствующие младшим разрядам, должны располагаться слева от ячеек старших разрядов. В этом случае порядок пересчета формул в ячейках будет обеспечивать распространение переноса от младшего к старшему разряду.
Моделирование вычислительного блока с помощью табличного процессора Microsoft Excel
Моделирование вычислительного блока, содержащего узлы с памятью, рассмотрим на примере операции деления чисел нацело. Для деления нацело 8-разрядного двоичного числа X на 8-разрядное двоичное число Y используется следующий алгоритм. Если число Y = 0 (специальный признак z = 1), то деление не выполняется. В противном случае из делимого X вычитается делитель Y, и если знак разности s = 0 (разность положительное число), то частное Z увеличивается на единицу, а разность выступает в качестве нового уменьшаемого на следующем шаге. Процесс вычитания продолжается до тех пор, пока не будет получена отрицательная разность (s = 1). В этом случае Z будет представлять собой искомое частное от деления X на Y нацело.
Пример схемы 8-разрядного вычислительного блока для выполнения операции деления чисел нацело, моделируемого на листе Microsoft Excel, приведен на рис. 5. Вычислительный блок включает: регистр делимого RX, регистр делителя RY, сумматор (вычитатель) SM, счетчик частного RZ и логический элемент ИЛИ-НЕ (для формирования признака z равенства нулю содержимого регистра RY). В регистр RX при подаче управляющего сигнала v1 заносится делимое: RX: = X, а при подаче сигнала v3 – содержимое сумматора: RX: = SM. В регистр RY при подаче управляющего сигнала v2 заносится делитель: RY: = Y. Результат вычитания из содержимого регистра RX содержимого регистра RY формируется в сумматоре при подаче управляющего сигнала v5: SM: = RX-RY. При этом формируется признак знака разности s, который равен единице, если результат отрицательный и нулю в противном случае. Все разряды сумматора, включая разряд s, устанавливаются в нулевые состояния при подаче управляющего сигнала v4: SM: = 0. К содержимому счетчика RZ можно добавить единицу с помощью управляющего сигнала v7: RZ: = RZ + 1, а с помощью сигнала v6 – установить в нулевое состояние (RZ: = 0).
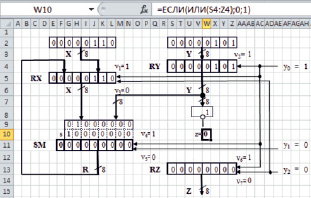
Рис. 5. Экранная форма функциональной модели 8-разрядного вычислительного блока деления чисел нацело
В вычислительном блоке используется сумматор (вычитатель) с последовательным переносом (заемом), работа которого описывается следующими булевыми функциями:
rn-1 = (xn-1⊕yn-1⊕pn-1),
gn = ?xn-1&yn-1∨?xn-1&gn-1∨yn-1&gn-1,
где xn-1 и yn-1 – разряды двоичных кодов уменьшаемого и вычитаемого соответственно; rn-1 – разряд разности, а gn – разряд заема; n = 1,…,8. g0 = 0. Разряд знака разности s = g8.
На рис. 5 над вычитателем (SM) отображается 8-разрядное слово разности r0r1r2r3r4r5r6r7, над которым выводится 8-разрядное слово заемов g0g1g2g3g4g5g6g7. Для корректной работы вычитателя с последовательным распространением заема разряды вычитателя по отношению к разрядам регистров располагаются в противоположном порядке, который затем восстанавливается в отображении разрядов сумматора (SM).
Микропрограмма деления чисел нацело для схемы, приведенной на рис. 5, состоит из трех различных микрокоманд (МК) и может быть представлена в следующем виде.
НАЧАЛО
МК 1: y1 = 1; y2 = 0; y3 = 0 (v1: RX: = X; v2: RY: = Y; v4: SM: = 0; v6: RZ: = 0);
если z = 1, то переход к КОНЕЦ, иначе
МК 2: y1 = 0; y2 = 1; y3 = 0 (v5: SM: = RX-RY);
если s = 1, то переход к КОНЕЦ, иначе
МК 3: y1 = 0; y2 = 0; y3 = 1 (v3: RX: = SM; v7: RZ: = RZ + 1); переход к МК 2
КОНЕЦ
В процессе экспериментальных исследований функциональной модели вычислительного блока осуществляется проверка правильности выполнения микропрограммы для всех сочетаний значений логических условий. В табл. 2 приведен пример выполнения микропрограммы по тактам для случая, когда делимое X = 00001111, а делитель Y = 000001001.
Таблица 2
Выполнение микропрограммы деления чисел нацело
|
Tакт |
МК |
y1y2y3 |
Микрооперации |
z |
s |
RX |
RY |
SM |
RZ |
|
1 |
1 |
100 |
RX: = X; RY: = Y; SM: = 0; RZ: = 0 |
0 |
0 |
00001111 |
000001001 |
00000000 |
00000000 |
|
2 |
2 |
010 |
SM: = RX-RY |
0 |
0 |
00001111 |
000001001 |
00000110 |
00000000 |
|
3 |
3 |
001 |
RX: = SM; RZ: = RZ + 1 |
0 |
0 |
00000110 |
000001001 |
00000110 |
00000001 |
|
4 |
2 |
010 |
SM: = RX-RY |
0 |
1 |
00000110 |
000001001 |
11111101 |
00000001 |
|
5 |
4 |
000 |
– |
0 |
1 |
00000110 |
000001001 |
11111101 |
00000001 |
В примере в процессе деления чисел нацело при первом вычитании делителя из делимого (такт 2, МК 2) получается положительный результат (s = 0) и частное увеличивается на единицу (МК 3). Второе вычитание делителя из полученной ранее разности (такт 4, МК 2) приводит к отрицательному результату (s = 1), и процесс деления завершается.
Заключение
Предлагаемый подход к функциональному моделированию узлов и блоков ЭВМ, представляющих собой последовательностные схемы, с помощью табличного процессора Microsoft Excel позволяет включить в учебный процесс самостоятельную разработку обучающимися простейших узлов и блоков ЭВМ с последующим построением и экспериментальным исследованием их программных моделей. В качестве достоинств такого подхода следует отметить: использование популярной инструментальной программы (Microsoft Excel); широкие возможности для формирования различных вариантов индивидуальных заданий при построении функциональных моделей; открытость для последующего развития и адаптации в зависимости от особенностей учебного процесса и предпочтений преподавателя.



