В среднесрочной перспективе основным средством навигационного обеспечения всех этапов полета воздушных судов (ВС) и посадки в соответствии категориям ICAO [1] станут спутниковые системы навигации (ССН), в том числе и российская система ГЛОНАСС. Однако на современном этапе развития ССН обладают недостаточными целостностью, помехоустойчивостью, а в ряде случаев – и точностью навигационно-временного поля (НВП), что снижает эффективность их применения именно для решения задач посадки ВС.
Для поддержки перспективных навигационных прикладных процессов [2] ССН нуждаются в функциональных дополнениях бортового (ABAS), спутникового (SBAS) или наземного (GBAS) базирования. Функциональные дополнения позволяют компенсировать некоторые недостатки ССН, в частности определить дифференциальные поправки к измеренным потребителями координатам [1]. Однако и они подвержены воздействию ряда дестабилизирующих факторов, поэтому применение SBAS/GBAS не в полной мере обеспечивает заданные показатели точности навигации по ССН. Так, например, в пределах зоны действия SBAS обеспечивается полет ВС по маршруту, в зоне аэродрома, а также заход на посадку с уровнями APV-I и APV-II. При этом операции захода на посадку APV-I и APV-II могут осуществляться только в определенных, назначенных областях, а не во всей зоне действия системы SBAS [3]. Проблемы же GBAS заключаются в ухудшении точности коррекции координат по мере удаления ВС от контрольно-корректирующей станции, а также в необходимости передачи цифровой информации (поправок) на большие расстояния. Для этого нужны каналы передачи данных с высокой пропускной способностью, что требует установки на борту ВС дополнительно аппаратуры приема дифференциальных поправок.
Одним из возможных способов повышения точности навигационных определений ССН является использование функционального дополнения в виде псевдоспутников (ПС). В традиционном представлении ПС представляют собой стационарные передающие устройства наземного базирования, или с базированием в околоземном пространстве (например, высокая мачта, воздушный шар), сигналы которых синхронизованы с сигналами ССН, а параметры сигналов и их формат близки или аналогичны параметрам и формату сигналов ССН [4, 5]. В зоне действия ПС создается интегрированное НВП с улучшенными в плане точности и надежности характеристиками по сравнению с первичным НВП ССН.
Анализ работ [6–8], посвященных проблемам использования ПС показал, что дополнение навигационных спутников (НС) ССН одним или сетью ПС, позволит улучшить геометрию в вертикальном канале, повысить информационную избыточность, что приведет к увеличению точности и надежности навигационных определений. Сформированное с использованием ПС интегрированное НВП может удовлетворить требованиям, предъявляемым к точности навигации ВС на этапе посадки.
При применении ПС возникает задача нахождения их оптимального размещения в зоне аэродрома для достижения максимальной точности интегрированного НВП ССН. В [1] показано, что ввиду изменения геометрии ССН с течением времени, оптимальное положение наземного ПС также будет изменяться. Поэтому, например, в работе [9] предлагается использовать мобильный ПС для достижения максимальной точности интегрированного НВП ГЛОНАСС на каждый момент времени.
Применение мобильного ПС наземного базирования сопряжено с рядом проблем, например, затенение их сигналов неровностями рельефа местности или объектами аэродрома, ограничения на скорость и зону перемещения и другими. Поэтому предлагается рассмотреть применение ПС, размещенного на беспилотном летательном аппарате (БПЛА), что существенно расширяет динамические свойства ПС и возможности устойчивого приема его сигналов [10], а также позволяет применить такой метод при заходах ВС на посадку по гибким траекториям. При этом необходимо решить задачу нахождения оптимальной траектории перемещения БПЛА в воздушном пространстве аэродрома.
Цель исследования: нахождение оптимальной траектории полета и оценка эффективности применения мобильного ПС, размещенного на борту БПЛА, для улучшения точности интегрированного НВП ГЛОНАСС путем уменьшения геометрического фактора (ГФ) в зоне аэродрома при заходе ВС на посадку по гибкой траектории.
Материалы и методы исследования
О точности интегрированного НВП можно судить по значениям пространственного геометрического фактора PDOP (Position Dilution of Precision) или его составляющим – вертикальному VDOP (Vertical Dilution of Precision) и горизонтальному HDOP (Horizontal Dilution of Precision) ГФ в точке наблюдения. При этом
PDOP2 = HDOP2 + VDOP2, (1)
а точность определения местоположения (горизонтальных координат) и точность определения высоты полета ВС связаны со значениями соответствующих ГФ выражениями
σr = σR?HDOP, σH = σR?VDOP,
где σr – среднеквадратическая погрешность (СКП) определения местоположения (радиальная СКП), σH – СКП определения высоты, σR – СКП определения псевдодальности до НС.
В работе [9] решена задача определения оптимального размещения стационарного ПС, при котором среднее значение VDOPср вдоль всей прямолинейной траектории снижения (глиссады) будет минимальным. Показано, что ввиду изменения положения НС относительно ВС из-за их орбитального движения, не существует единственного оптимального положения ПС, обеспечивающего минимальный ГФ, в рассматриваемом случае – VDOPср.
При достаточно хороших (не более 2–2,5) значениях вертикального ГФ применение ПС, размещенного в типовой точке (не оптимально) позволяет улучшить VDOPср на 22–25 %. Размещение ПС в оптимальных для рассматриваемых моментов времени точках позволит уменьшить VDOPср на 7–9 % по сравнению с его размещением в типовой точке.
Предложенная в [9] методика нахождения единственного (квазиоптимального) положения стационарного ПС позволяет уменьшить VDOPср на 3–4 %. Отсюда следует вывод, что для обеспечения минимального значения ГФ на всей траектории посадки ВС необходимо использовать мобильный ПС, размещенный на БПЛА. При этом БПЛА должен перемещаться по оптимальной траектории, образованной совокупностью точек, в которых достигается минимальное значение ГФ для каждого момента времени решения задачи оптимизации.
Для проведения исследований методами математического моделирования в среде графического программирования LabView были выбраны следующие исходные данные:
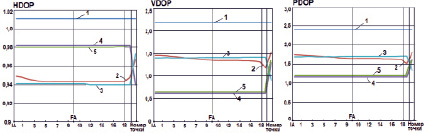
– координаты центра взлетно-посадочной полосы (ВПП) аэродрома посадки 71,927 с.ш., 114,08 в.д., высота над уровнем Мирового океана 30 м, UTC + 9, курс ВПП 174,22 град;
– траектория захода ВС на посадку (рис. 1): криволинейная (высота 600 м) на участке от точки IA (Initial Approach) до точки FA (Final Approach), расположенной на удалении 10 км от начала ВПП; прямолинейная углом наклона глиссады 3 град. – на участке от FA до касания ВПП; скорость ВС на всей траектории 250 км/час;
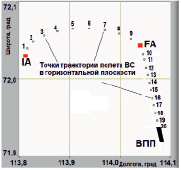

а) б)
Рис. 1. Траектория полета ВС в горизонтальной (а) и вертикальной (б) плоскостях
– начальное положение БПЛА (мобильного ПС) в горизонтальной плоскости совпадает с точкой IA, скорость БПЛА равна скорости ВС на посадочной траектории;
– задача оптимизации решалась методом Хука – Дживса в выбранных 22 дискретных точках траектории полета ВС, разделенных временным интервалом полета между ними 10 с.
Задача нахождения оптимальной траектории полета БПЛА решалась в горизонтальной плоскости (рассматривался его полет на фиксированной высоте) и в пространстве (с изменением высоты полета). В качестве критерия оптимизации использовался минимум ГФ (либо пространственного PDOP, либо горизонтального HDOP, либо вертикального VDOP) для навигационных определений на ВС:
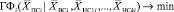 ,
,
где 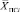 – искомый вектор координат БПЛА в i-й точке траектории в i-й момент времени,
– искомый вектор координат БПЛА в i-й точке траектории в i-й момент времени, 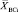 – известные координаты ВС в i-й точке траектории в i-й момент времени,
– известные координаты ВС в i-й точке траектории в i-й момент времени, 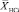 – известные координаты НС, находящихся в зоне видимости, k – количество видимых НС.
– известные координаты НС, находящихся в зоне видимости, k – количество видимых НС.
При расчете ГФ координаты БПЛА, ВС и НС представлены в прямоугольной геоцентрической системе координат. Поскольку оптимальная траектория полета БПЛА строится в геодезической системе координат (широта, долгота, высота), используются координатные преобразования из геодезической в прямоугольную геоцентрическую систему координат [1].
В процессе исследований необходимо определить, как влияют на результат решения задачи оптимизации выбор используемого критерия (минимум PDOP, HDOP или VDOP), высоты полета БПЛА и ВС, метод решения задачи – на плоскости или в пространстве.
Результаты исследования и их обсуждение
Для достижения поставленных целей исследований методами математического моделирования были проведены вычислительные эксперименты, которые отличались вариантами применения мобильного ПС и использованием различных критериев оптимизации.
Оценка влияния критерия оптимизации на значения ГФ при полете БПЛА по оптимальной траектории
Рассмотрены следующие ситуации:
– ПС отсутствует, и навигационные определения выполняются только по НС, находящимся в зоне видимости;
– ПС размещен в типовой точке на земле (точка расположения среднего маркерного радиомаяка), удаленной на расстояние 1 км от начала ВПП и на продолжении ее оси;
– мобильный ПС размещен на БПЛА, выполняющем полет на высоте 50 м.
На рис. 2 представлены графики изменения ГФ на траектории захода на посадку и посадки ВС для HDOP (рис. 2, а), VDOP (рис. 2, б) и PDOP (рис. 2, в). На рисунках: 1 – отсутствие ПС и решение навигационной задачи только по наблюдаемым НС; 2 – ПС размещен в типовой точке; 3, 4, 5 – мобильный ПС, оптимизация соответственно по HDOP, VDOP и PDOP.
а) б) в)
Рис. 2. Изменение значений ГФ в точках траектории захода на посадку и посадки ВС
Анализ полученных результатов показывает, что применение наземного ПС, расположенного в типовой точке, позволяет улучшить HDOP с 1,01 до 0,94, а VDOP – с 2,2 до 1,5 в точке IA и до 1,2 при пролете ВС над ПС. После пролета над ПС HDOP и VDOP ухудшаются до значений HDOP = 0,97 и VDOP = 1,55.
Применение мобильного ПС при оптимизации по минимуму HDOP дает незначительный выигрыш в значении HDOP (на 0,002–0,004) и незначительное ухудшение в значении VDOP (на 0,3–0,5) по сравнению с применением ПС, размещенного в типовой точке. При снижении ВС ниже ПС (Hпс > Hвс) наблюдается ухудшение HDOP (на 0,04–0,05) и улучшение VDOP (на 0,5). Таким образом, можно заключить, что эффективность применения мобильного ПС критична к соотношению высот полета ВС и БПЛА.
Оптимизация траектории БПЛА по минимуму VDOP и минимуму PDOP дает практически совпадающие результаты. Это обусловлено тем, что в ССН величина VDOP всегда больше, чем HDOP, поэтому и ее вклад в PDOP (см. выражение (1)) будет определяющим.
При оптимизации траектории полета БПЛА по минимуму VDOP значение HDOP будет незначительно хуже (примерно на 0,04), в то время, как значение VDOP значительно улучшится (на 0,7–0,8), чем при использовании ПС, размещенного в типовой точке.
При снижении ВС, когда выполняется условие Hвс < Hпс, наблюдается улучшение HDOP (примерно на 0,04) и ухудшение VDOP (примерно на 0,8).
Таким образом, можно заключить, что при оптимизации траектории полета БПЛА целесообразно использовать критерий минимума PDOP или минимума VDOP, что обеспечит наилучшую точность определения высоты полета и высокую точность определения горизонтальных координат ВС на большей части траектории захода на посадку и посадки. Для этого необходимо использовать маловысотный БПЛА, поскольку при снижении ВС ниже высоты полета БПЛА эффективность применения мобильного ПС будет снижаться.
Оценка влияния критерия оптимизации на построение оптимальной траектории полета БПЛА
Рассмотрим ситуацию, когда БПЛА выполняет полет на высоте 50 м, задача оптимизации его траектории решается в плоскости при отсутствии ограничений на область допустимых оптимальных положений БПЛА.
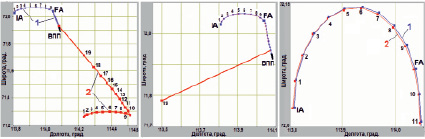
На рис. 3, а, рис. 3, б, представлены результаты решения задачи оптимизации при использовании в качестве критерия оптимизации соответственно минимума HDOP и PDOP. На рис. 3, в показана криволинейная часть траектории полета ВС (кривая 1) и БПЛА (кривая 2) в укрупненном масштабе.
а) б) в)
Рис. 3. Траектории полета БПЛА и ВС в горизонтальной плоскости
При оптимизации по минимуму HDOP смещение точек траекторий БПЛА и ВC при полете на постоянной высоте до точки FA составляет около 88 км, при этом форма траектории полета БПЛА повторяет форму траектории ВС (рис. 3, а, участки траекторий с т. 1 до т. 9). При снижении ВС с точки FA, оптимальная траектория полета БПЛА приближается к траектории ВС, совпадая с ней в точке, расположенной на высоте 50 м (когда Hвс = Hпс).
При оптимизации по минимуму PDOP оптимальная траектория полета БПЛА близка к траектории ВС (смещение в горизонтальной плоскости составило 80 м на участке постоянной высоты полета ВС до точки FA). На участке снижения ВС смещение траектории полета БПЛА уменьшалось с 80 м до 7 м. При Hвс < Hпс (вблизи ВПП), оптимальная точка траектории полета БПЛА сместилась на расстояние более 20 км.
Аналогичные эксперименты, проведенные для других интервалов времени, показали, что, ввиду изменения группировки НС, находящихся в зоне видимости, смещение оптимальной траектории полета БПЛА в горизонтальной плоскости изменяется, например уменьшилось и составило 35 м на участке полета до точки FA и 3 м вблизи ВПП. При этом сохраняется описанный выше характер уменьшения величины смещения на этапе снижения ВС.
Очевидно, что реализация полета реального БПЛА с ПС на борту по оптимальной траектории на заключительном этапе, когда происходит ее резкое смещение, практически невозможна. Поэтому полет БПЛА по оптимальной траектории должен заканчиваться в точке, совпадающей по высоте с высотой полета ВС на этапе снижения.
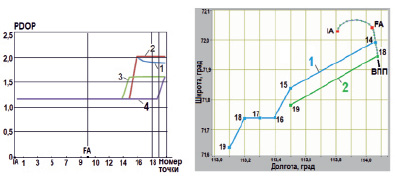
Для определения наиболее рациональной (с точки зрения обеспечения минимального или близкого к минимальному значения PDOP) траектории полета БПЛА при выполнении условия Hвс < Hпс (конечный участок траектории посадки), проведены исследования, результаты которых представлены на рис. 4, а, для следующих ситуаций:
а) б)
Рис. 4. Изменение PDOP (а) и оптимальная траектория полета БПЛА (б)
– БПЛА летит по оптимальной траектории на высоте 300 м до точки FA начала снижения ВС, затем зависает в точке FA (кривая 1);
– БПЛА летит по оптимальной траектории на высоте 300 м до точки FA начала снижения ВС, затем продолжает полет по прямолинейной траектории, проходящей на высоте 300 м над посадочной траекторией ВС (кривая 2);
– БПЛА летит по оптимальной траектории на высоте 300 м (кривая 3), задача оптимизации решается в горизонтальной плоскости;
– БПЛА летит по оптимальной траектории на высоте 300 м (кривая 4), задача оптимизации решается в пространстве, при этом высота полета БПЛА ограничена значением 50 м, снижение БПЛА может происходить с шагом 10 м на каждом цикле оптимизации.
Как следует из рис. 4, а, минимальное значение PDOP = 1,2 достигается практически вдоль всей траектории захода на посадку и посадки ВС при решении задачи оптимизации в пространстве (кривая 4). Ввиду невозможности реализовать полет БПЛА по оптимальной траектории после снижения ВС до высоты Hвс = Hпс можно рекомендовать зависание БПЛА в районе точки совпадения высот траекторий БПЛА и ВС (с учетом обеспечения безопасности их взаимного положения). При этом величина PDOP возрастает до 1,8, но остается меньше на конечном участке траектории посадки ВС, чем при других траекториях полета БПЛА.
На рис. 4, б, показаны траектории полета БПЛА при решении задачи оптимизации по критерию минимума PDOP в горизонтальной плоскости (кривая 1, высота Hпс = 300 м) и в пространстве (кривая 2, БПЛА может снижаться до высоты 50 м). Как следует из полученных результатов, когда Hвс < Hпс, оптимальная траектория (кривая 1) смещается относительно траектории ВС, и тем сильнее, чем ниже высота полета ВС. При решении задачи оптимизации в пространстве при снижении ВС оптимальная траектория полета БПЛА (кривая 2) также снижается, при этом располагаясь под траекторией ВС. После достижения высоты 50 м (ограничение высоты полета БПЛА) оптимальная траектория существенно смещается в горизонтальной плоскости относительно траектории ВС.
Влияние затенений НС объектами местности на построение оптимальной траектории полета ПС
В реальных условиях прием сигналов от всех НС, находящихся в зоне видимости ВС, может стать невозможным ввиду, например, затенений сигналов от НС неровностями рельефа местности или высотными объектами. Такая ситуация весьма вероятна при расположении аэродромов в горной местности, а также в зоне мегаполисов.
Рассмотрим влияние затенений сигналов НС для следующих условий:
– оптимизация траектории БПЛА осуществляется в горизонтальной плоскости при высоте полета БПЛА 300 м и 50 м, критерий оптимизации – минимум PDOP;
– наличие затенений будем учитывать введением угла маски 15 град и 30 град в программу моделирования орбитальной группировки ГЛОНАСС и выбора рабочего созвездия НС [11]. В штатном режиме работы приемника ССН угол маски равен 5 град.
Результаты исследований представлены на рис. 5, а (Hпс = 50 м) и рис. 5, б (Hпс = 300 м), где кривые 1, 2, 3 соответствуют углам маски 5, 15 и 30 град.
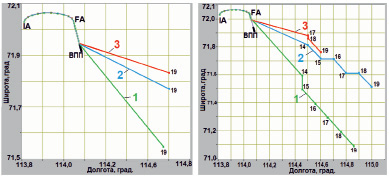
а) б)
Рис. 5. Оптимальные траектории полета БПЛА при затенениях НС ГЛОНАСС
Как видно из представленных результатов, оптимальная траектория ПС зависит от высоты его полета относительно ВС и наличия затенений. При Hпс < Hвс оптимальная траектория полета БПЛА проходит под траекторией полета ВС, а при Hпс > Hвс смещается в горизонтальной плоскости, причем смещение увеличивается по мере увеличения разности высот. При увеличении влияния затенений (соответствует увеличению угла маски) смещение оптимальной траектории БПЛА относительно траектории ВС уменьшается.
Анализ данных по оценке значения PDOP показал, что в условиях эксперимента увеличение угла маски с 5 до 30 град. привело к увеличению PDOP с 2,2 до 2,9 при отсутствии ПС. Применение мобильного ПС, движущегося по оптимальной траектории, позволяет уменьшить PDOP до 1,2 (угол маски 5 град) и 1,7 (угол маски 30 град), т.е. в 1,83 и 1,7 раз соответственно. Однако на заключительном этапе посадки, когда Hпс > Hвс , выигрыш от применения мобильного ПС уменьшается.
Следует также отметить, что в исследуемом диапазоне высот (от 50 до 300 м) обеспечивается практически одинаковое значение PDOP независимо от высоты полета БПЛА с установленным на нем ПС при выполнении условия Hпс < Hвс.
Заключение
Проведенные исследования показали, что применение мобильного ПС, размещенного на борту БПЛА, движущегося по оптимальной траектории, позволяет повысить точность интегрированного НВП на 5–7 % по сравнению с другими способами применения ПС.
При этом рекомендуется:
– в качестве инструментария для построения оптимальной траектории БПЛА использовать метод Хука – Дживса, отличающийся приемлемыми вычислительными затратами;
– в качестве критерия оптимизации использовать минимум пространственного ГФ PDOP;
– выполнять полет БПЛА на возможно более низких высотах;
– для обеспечения высокой точности интегрированного НВП на заключительном этапе посадки (когда Hвс < Hпс) использовать режим зависания БПЛА.
Следует также отметить, что применение мобильного ПС позволит существенно ослабить такой недостаток применения ПС, как эффект «дальний – ближний» [11], поскольку изменение расстояния между ПС и определяющимся ВС будет значительно меньшим, чем при использовании стационарного ПС.
Работа выполнена при финансовой поддержке проектов РФФИ грант № 19-08-00010.



