Рассматривая вопросы соблюдения высокого уровня надежности инженерно-технических сетей, необходим анализ показателей и статистических данных, полученных в ходе проведения испытаний или эксплуатации. В процессе испытаний и эксплуатации оборудования статистические данные позволяют отслеживать статику и динамику изменения количественных характеристик надежности [1]. В большинстве случаев при испытаниях или эксплуатации оборудования (или элементов системы) важной характеристикой принято считать время наработки до момента наступления полного отказа. При этом в инженерной практике расчетов учитывают характеристики, востребованные для определения и последующего применения вероятностных показателей. Одним из инструментов выработки решений о сохранении высокого уровня надежности [2] можно считать системный анализ, создание математических моделей и разработку методов расчета количества информации [3, 4], характеризующего состояние системы. В основу данных инструментов положены идеи Р. Хартли, А.Н. Колмогорова и классическая теория К. Шеннона [5] о получении количества информационной энтропии (меры неопределенности информации), которая выражается универсальной формулой вида p·log p, где p – вероятность состояния элемента системы. Данная классическая формула, по мнению многих ученых, является универсальной [6].
Цель исследования заключается в выявлении применимости совместного использования показателей надежности и информационной энтропии в решении задач обеспечения заданного уровня надежности инженерно-технических сетей.
Рассмотрим далее процесс анализа и роста событий в системе.
Анализ процесса роста событий в системе
Говоря о вероятностной природе вариации состояний инженерных сетей, необходимо отметить: применительно к возможностям системного анализа выделяют аддитивный рост (связанный с операцией сложения) и мультипликативный рост (основанный на операции умножения). Рост может характеризоваться множеством показателей, одним из которых будем считать событие, переводящее элемент из одного состояния в другое – противоположное. По сути событие – это внезапный отказ, выводящий оборудование из строя.
Рассматривая рост, связанный с прибавлением количества появляющихся событий, речь идет о потоковом процессе, вне зависимости от того, аддитивный это или мультипликативный процесс. Такой потоковый процесс определяет скорость роста количества событий N, которая прямо пропорциональна его текущему значению: ΔN = k·N, где k – некоторая постоянная. С позиции динамики изменения данного показателя будем иметь
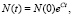(1)
где N(0) – количественная величина в начальный момент времени, C – показатель, относящийся к динамике появления событий.
Рассмотрим данный рост с целью получения вероятностной характеристики. Пусть p(x)·dx – это доля или вероятность событий/отказов, лежащая в промежутке между x и x + dx. Если её гистограмма представляет собой прямую линию в двойных логарифмических координатах, тогда ln p(x) = – α ln x + C, где α и С – константы. В данном математическом представлении видна следующая закономерность: гистограмма, построенная в таких координатах, представляет собой прямую линию. Такое утверждение связано с именем Зипфа (Ципфа) [7]. Закон Ципфа является одним из базовых законов, используемых при измерении количественных характеристик информации, когда вероятность определяется через частоту появления событий и полное количество событий. Тем самым от уравнения (1) можно перейти к вероятностной характеристике:
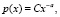(2)
где C = eC.
Распределение вида (2) – степенной закон. Здесь константа α является показателем степенного закона и имеет фиксированное значение, тогда как константа С не играет существенной роли, поскольку она определяется из требования: сумма распределения p(x) должна быть равна 1.
Экспонента (2) согласуется с экспонентой распределения вероятности безотказной работы элемента i системы:
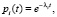(3)
где λi – интенсивность отказа элемента i, количественные характеристики надежности которого известны достоверно.
Величина pi(t) может быть определена исходя из данных, полученных в результате испытаний, эксплуатации и обработки экспертных оценок о надежности нового оборудования.
Выражение (3), отражающее справедливость экспоненциального закона надежности, построено на допущениях о том, что отказы являются событиями случайными и независимыми, отказ любого элемента приводит к отказу всей системы, а интенсивность отказов является величиной постоянной.
Если известно, что отказы элементов появляются последовательно, то вероятность безотказной работы системы при испытаниях определится по выражению
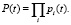(4)
В свою очередь интенсивность отказов пропорциональна размеру системы, тогда интенсивность отказа системы можно вычислить по формуле
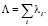(5)
Согласно (3), вероятность безотказной работы системы:
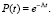(6)
Третьим статистическим параметром расчета является среднее время безотказной работы элемента i:
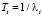, (7)
тогда среднее время безотказной работы системы:
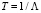или 
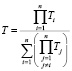, (8)
где n – количество рассматриваемых элементов.
Рассматривая аддитивный рост, сложение показателей указывает на наличие принципа роста и, как следствие, независимости событий между элементами системы. Напротив, операция умножения, относящаяся к мультипликативному росту, подтверждает наличие событий, обусловленных возникновением внешних и внутренних факторов. Анализ мультипликативного роста в системе может быть полезен при выявлении слабых звеньев в её структуре. Однако не стоит забывать о том, что вышеизложенное об аддитивном и мультипликативном росте относится к идеальным случаям. Тем не менее вероятностный мультипликативный рост в пределе приводит к экспоненциальному частотному распределению вероятности, независимо от исходной формы распределения множества, что подтверждает справедливость применения математических выражений (3) и (6).
Модель определения состояния сети
В большинстве случаев структура распределительной сети имеет вид дерева, которое формируется следующим образом: строятся ветви (связи) от источника энергии до конечного потребителя или потребителей. Такое дерево можно представить в виде ацикличного графа G = (U, X), в котором U – множество вершин (вершины имитируют единственный источник и потребители), X – множество дуг (имитируют связующие элементы сети).
Имея граф сети, предстоит определить меру неопределенности информации для работоспособного и неработоспособного состояний всех элементов. При этом используется классическая модель К. Шеннона, позволяющая определять информацию I с её разграничением по качественному признаку [8] согласно следующей формуле:
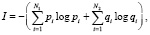
при условии
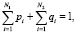(9)
где pi и qi = 1 – pi – вероятности работоспособного и неработоспособного состояний элемента i (определяемые исходя из статистической обработки данных: частота отказов; время наработки на отказ; время восстановления и др.), N1 и N2 – количество работоспособных и неработоспособных состояний элемента.
Выражение (9) справедливо при условии, что события (например, отказы оборудования сети) имеют случайную природу, независимы друг от друга и большинство из них подчинено статистическим законам распределения.
Одна из задач, решение которой необходимо как при проектировании, так и при эксплуатации сети, касается вопросов структурной оптимизации, которая сводится к определению значения целевой функции min <ci, xi> линейного вида. Что касается ограничений (в виде неравенств), накладываемых на задачу, то их построение является сложной задачей. Поскольку граф имеет форму дерева, то его каждая ветвь – параллельно-последовательное соединение элементов (дуг), в котором параллельное соединение отображает резервирование [9, 10]. По сути, ветвь – отдельно рассматриваемый (от дерева) граф, состоящий из путей и сечений. Входящая в уравнение ограничения задачи энтропия ветви определяется через вероятности работоспособного и неработоспособного состояний элементов, что в последующем позволяет обратиться к расчетам количества энтропии. Её поиск целиком зависит от имеющихся в распоряжении показателей надежности.
Для построения уравнений ограничений задачи оптимизации можно воспользоваться математическими уравнениями, предложенными в [11]. На их основе и согласно теореме сложения и умножения вероятностей, составим математическое выражение энтропии ветви. Математическая модель имеет следующий вид:
(10)
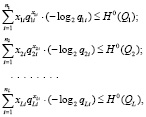(11)
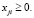
В предложенной модели: L – количество рассматриваемых путей распределительной сети; nj – количество сечений (элементов) ветви j;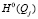 
– граничное значение энтропии неработоспособного состояния ветви j; cji – стоимость элемента i, входящего в путь j.
Модель (10)–(11) описывает поиск оптимальной структуры сети, когда в одной задаче востребованы как показатели надежности, так и информационная энтропия, значения которой получены исходя также из параметров надежности. Существуют способы расчетов, которые позволяют выразить показатели надежности оборудования сети через величину энтропии. Далее рассмотрим один из них.
Пример расчета показателей надежности и энтропии
Пусть имеется оборудование (необходимое для участия в работе инженерно-технической сети), которое подлежит испытаниям на надежность. После проведения первичных испытаний на отказ оборудования (или элементы испытаний) можно определить частную энтропию работоспособного состояния: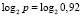 
и неработоспособного состояния: 
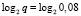. Для проведения повторной проверки на надежность взята партия из 1000 однотипных элементов. Пусть испытания проводились в течение 10000 часов. В течение первых 6000 часов отказало 55 элементов, за последующие 4000 часов отказало 30 элементов. Требуется определить составляющие энтропии на интервалах [0; 6000] → Δ1 и [6000; 10000] → Δ2 часов и сопоставить их между собой для выявления степени надежности.
Решение. Предварительно вычислим вероятности на рассматриваемых интервалах времени:
– вероятность безотказной работы на интервале Δ1: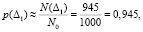 
где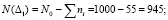 
– вероятность безотказной работы на интервале Δ2: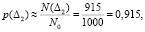 
где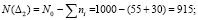 
– вероятность отказа на интервале Δ1: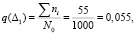 
– вероятность отказа на интервале Δ2: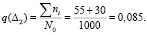 
Для каждого рассматриваемого интервала выполняется условие: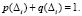 
Информационная энтропия на интервале Δ1:
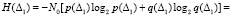
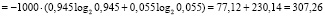бит. (12)
Информационная энтропия на интервале Δ2:
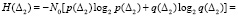
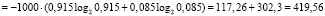бит. (13)
Сопоставляя количественные величины энтропии, полученные согласно (12) и (13) на рассматриваемых интервалах времени, видно следующее: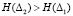 
поскольку с увеличением числа отказавших элементов энтропия растет и стремится к максимуму при равенстве противоположных вероятностей:
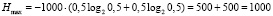бит.
Выполним данный расчет, используя формулу 14 для определения энтропии состояния системы на рассматриваемом интервале времени Δt: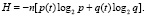 
Расчет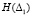 
по выражению (12) остается без изменений, поскольку вероятности первичных и последующих испытаний на интервале [0; 6000] совпадают.
Информационная энтропия на интервале Δ2:
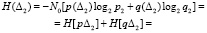
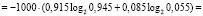
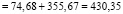бит. (14)
Сопоставляя значения энтропии, полученные из (12) и (14), отметим следующее: рост числа отказов, с одной стороны, указывает на снижение вероятности безотказной работы,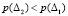 
и уменьшение энтропии, 
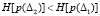, с другой – увеличивает вероятность отказа и приводит к росту энтропии 
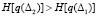. Тем самым снижение уровня надежности испытуемых элементов связано с ростом энтропии неработоспособного состояния и снижением работоспособного.
Заключение
Описанный в работе подход, со ссылкой на ранее выполненные работы, касается ряда вопросов, связанных с представлением показателей надежности оборудования инженерно-технических сетей через меру неопределенности информации. Решение таких задач как структурная оптимизация, выбор эффективных схем, предполагает наличие ряда последовательных решений: сбор и обработка статистических данных надежности оборудования; анализ динамики показателей состояния оборудования; определение величины энтропии (которая в данном случае получила название статистическая энтропия). Совместное применение показателей надежности и энтропии позволяет выявлять тенденции роста показателей состояния сети, оценивать степень состояния элементов и уровень надежности сети, строить простейшие тренды. Реализация мероприятий по обеспечению надежности сетей позволит обеспечить повышение экономической эффективности работы инженерных сетей за счет экономии финансовых средств на издержках, связанных с выявлением и преднамеренным устранением нежелательных последствий.
Работа выполнена при поддержке Фонда содействия инновациям по программе «УМНИК» в рамках договора № 13138ГУ/2018 от 23.05.2018.